scipy.stats.

tukey_hsd#

scipy.stats.tukey_hsd(*args, equal_var=True)[источник]#

Выполнить тест Тьюки HSD на равенство средних по нескольким обработкам.

Тест Тьюки на честно значимые различия (HSD) выполняет попарное сравнение средних для набора образцов. В то время как ANOVA (например, f_oneway) оценивает, идентичны ли истинные средние значения, лежащие в основе каждой выборки. HSD Тьюки — это апостериорный тест, используемый для сравнения среднего значения каждой выборки с средним значением каждой другой выборки.

Нулевая гипотеза состоит в том, что распределения, лежащие в основе выборок, имеют одинаковое среднее значение. Тестовая статистика, которая вычисляется для каждой возможной пары выборок, представляет собой просто разность между выборочными средними. Для каждой пары p-значение — это вероятность при нулевой гипотезе (и других предположениях; см. примечания) наблюдать такое экстремальное значение статистики, учитывая, что выполняется множество попарных сравнений. Также доступны доверительные интервалы для разности между каждой парой средних.

Параметры:

sample1, sample2, …array_like: Выборочные измерения для каждой группы. Должно быть не менее двух аргументов.
equal_var: bool, необязательный: Если True (по умолчанию) и размер выборки одинаков, выполняется тест Тьюки-ХСД [6]. Если True и размер выборки разный, выполняется тест Тьюки-Крамера [4]. Если False, выполнить тест Games-Howell [7], который не предполагает равные дисперсии.

Возвращает:

результатTukeyHSDResult экземпляр

Возвращаемое значение — объект со следующими атрибутами:

статистикаfloat ndarray: Вычисленная статистика теста для каждого сравнения. Элемент с индексом (i, j) является статистикой для сравнения между группами i и j.
p-значениеfloat ndarray: Вычисленное p-значение теста для каждого сравнения. Элемент с индексом (i, j) является p-значением для сравнения между группами i и j.

Объект имеет следующие методы:

confidence_interval(confidence_level=0.95):: Вычислить доверительный интервал для указанного уровня доверия.

Смотрите также

dunnett: выполняет сравнение средних с контрольной группой.

Примечания

Использование этого теста основывается на нескольких предположениях.

Наблюдения независимы внутри и между группами.
Наблюдения внутри каждой группы распределены нормально.
Распределения, из которых взяты выборки, имеют одинаковую конечную дисперсию.

Исходная формулировка теста была для выборок равного размера, взятых из популяций, предполагаемых с равными дисперсиями [6]. В случае неравных размеров выборок тест использует метод Тьюки-Крамера [4]. Когда равные дисперсии не предполагаются (equal_var=False), тест использует метод Геймса-Хауэлла [7].

Ссылки

[1]

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.7.1. Метод Тьюки.” https://www.itl.nist.gov/div898/handbook/prc/section4/prc471.htm, 28 ноября 2020.

[2]

Абди, Эрве и Уильямс, Линн. (2021). «Честно значимый различие Тьюки (HSD) тест.» https://personal.utdallas.edu/~herve/abdi-HSD2010-pretty.pdf

[3]

“Однофакторный дисперсионный анализ с использованием SAS PROC ANOVA & PROC GLM.” SAS Tutorials, 2007, www.stattutorials.com/SAS/TUTORIAL-PROC-GLM.htm.

[4] (1,2)

Крамер, Клайд Янг. «Расширение множественных ранговых тестов на групповые средние с неравным числом повторений». Biometrics, том 12, № 3, 1956, стр. 307-310. JSTOR, www.jstor.org/stable/3001469. Доступ 25 мая 2021.

[5]

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.3.3. Таблица ANOVA и проверка гипотез о средних” https://www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm, 2 июня 2021.

[6]

Тьюки, Джон У. "Сравнение индивидуальных средних в анализе дисперсии." Biometrics, том 5, номер 2, 1949, стр. 99-114. JSTOR, www.jstor.org/stable/3001913. По состоянию на 14 июня 2021.

[7] (1,2)

P. A. Games и J. F. Howell, "Pairwise Multiple Comparison Procedures with Unequal N’s and/or Variances: A Monte Carlo Study," Journal of Educational Statistics, vol. 1, no. 2, pp. 113-125, Jun. 1976, doi: https://doi.org/10.3102/10769986001002113.

Примеры

Вот некоторые данные, сравнивающие время облегчения трех марок лекарств от головной боли, указанное в минутах. Данные адаптированы из [3].

>>> import numpy as np
>>> from scipy.stats import tukey_hsd
>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]

Мы хотели бы проверить, различаются ли средние значения между любыми из групп статистически значимо. Сначала визуально исследуем диаграмму размаха.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.boxplot([group0, group1, group2])
>>> ax.set_xticklabels(["group0", "group1", "group2"]) 
>>> ax.set_ylabel("mean") 
>>> plt.show()

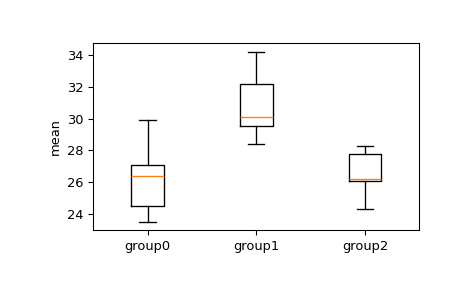
../../_images/scipy-stats-tukey_hsd-1_00_00.png

Из диаграммы «ящик с усами» мы видим перекрытие межквартильных диапазонов группы 1 с группой 2 и группой 3, но мы можем применить tukey_hsd тест для определения, является ли разница между средними значимой. Мы устанавливаем уровень значимости .05 для отклонения нулевой гипотезы.

>>> res = tukey_hsd(group0, group1, group2)
>>> print(res)
Pairwise Group Comparisons (95.0% Confidence Interval)
Comparison  Statistic  p-value  Lower CI  Upper CI
 (0 - 1)     -4.600     0.014    -8.249    -0.951
 (0 - 2)     -0.260     0.980    -3.909     3.389
 (1 - 0)      4.600     0.014     0.951     8.249
 (1 - 2)      4.340     0.020     0.691     7.989
 (2 - 0)      0.260     0.980    -3.389     3.909
 (2 - 1)     -4.340     0.020    -7.989    -0.691

Нулевая гипотеза состоит в том, что каждая группа имеет одинаковое среднее значение. P-значение для сравнений между group0 и group1 а также group1 и group2 не превышают 0.05, поэтому мы отвергаем нулевую гипотезу о том, что они имеют одинаковые средние. P-значение сравнения между group0 и group2 превышает .05, поэтому мы принимаем нулевую гипотезу о том, что нет значимой разницы между их средними значениями.

Мы также можем вычислить доверительный интервал, связанный с выбранным уровнем доверия.

>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]
>>> result = tukey_hsd(group0, group1, group2)
>>> conf = res.confidence_interval(confidence_level=.99)
>>> for ((i, j), l) in np.ndenumerate(conf.low):
...     # filter out self comparisons
...     if i != j:
...         h = conf.high[i,j]
...         print(f"({i} - {j}) {l:>6.3f} {h:>6.3f}")
(0 - 1) -9.480  0.280
(0 - 2) -5.140  4.620
(1 - 0) -0.280  9.480
(1 - 2) -0.540  9.220
(2 - 0) -4.620  5.140
(2 - 1) -9.220  0.540