scipy.signal.

czt#

scipy.signal.czt(x, m=None, w=None, a=1 + 0j, *, ось=-1)[источник]#

Вычислить частотную характеристику вокруг спирали в Z-плоскости.

Параметры:

xмассив: Сигнал для преобразования.
mint, необязательный: Желаемое количество выходных точек. По умолчанию равно длине входных данных.
wcomplex, опционально: Соотношение между точками на каждом шаге. Это должно быть точно, иначе накопленная ошибка ухудшит хвост выходной последовательности. По умолчанию равноудаленные точки по всей единичной окружности.
acomplex, опционально: Начальная точка в комплексной плоскости. По умолчанию 1+0j.
осьint, необязательный: Ось, по которой вычисляется БПФ. Если не задана, используется последняя ось.

Возвращает:

выходndarray: Массив тех же размерностей, что и x, но с длиной преобразованной оси, установленной в m.

Смотрите также

CZT: Класс, создающий вызываемую функцию Z-преобразования чирпа.
zoom_fft: Удобная функция для частичных вычислений БПФ.

Примечания

Значения по умолчанию выбраны так, чтобы signal.czt(x) эквивалентно fft.fft(x) и, если m > len(x), что signal.czt(x, m) эквивалентно fft.fft(x, m).

Если преобразование нужно повторить, используйте CZT для создания специализированной функции преобразования, которую можно повторно использовать без перевычисления констант.

Пример применения — в идентификации систем, многократное вычисление небольших срезов z-преобразования системы вокруг ожидаемого положения полюса для уточнения оценки истинного местоположения полюса. [1]

Ссылки

[1]

Steve Alan Shilling, «A study of the chirp z-transform and its applications», стр. 20 (1970) теперь выдают информативную ошибку на пустой ввод вместо достижения предела рекурсии.

Примеры

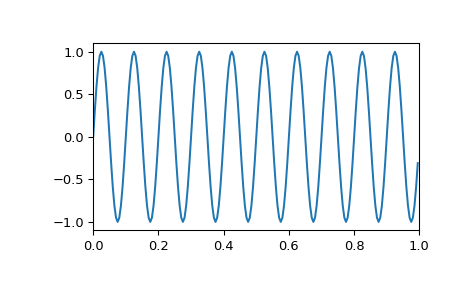
Сгенерировать синусоиду:

>>> import numpy as np
>>> f1, f2, fs = 8, 10, 200  # Hz
>>> t = np.linspace(0, 1, fs, endpoint=False)
>>> x = np.sin(2*np.pi*t*f2)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

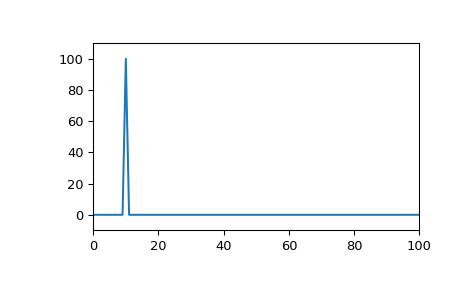
Его дискретное преобразование Фурье содержит всю энергию в одной частотной ячейке:

>>> from scipy.fft import rfft, rfftfreq
>>> from scipy.signal import czt, czt_points
>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

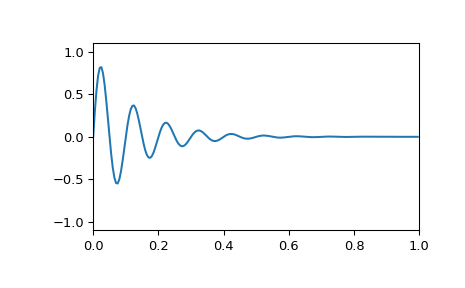
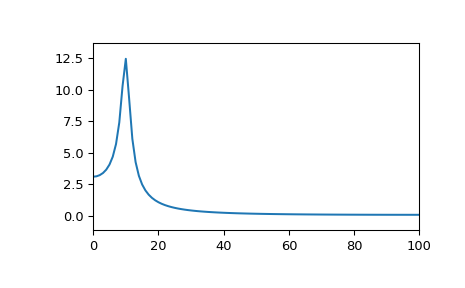
Однако, если синусоида затухает логарифмически:

>>> x = np.exp(-t*f1) * np.sin(2*np.pi*t*f2)
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

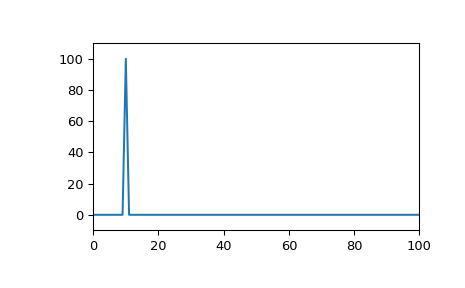
ДПФ будет иметь спектральное просачивание:

>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

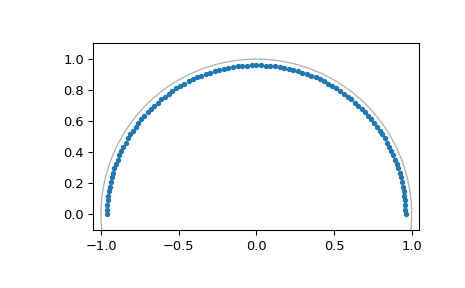
В то время как ДПФ всегда берёт отсчёты z-преобразования по единичной окружности, z-преобразование чирпа позволяет брать отсчёты Z-преобразования вдоль любой логарифмической спирали, например, окружности с радиусом меньше единицы:

>>> M = fs // 2  # Just positive frequencies, like rfft
>>> a = np.exp(-f1/fs)  # Starting point of the circle, radius < 1
>>> w = np.exp(-1j*np.pi/M)  # "Step size" of circle
>>> points = czt_points(M + 1, w, a)  # M + 1 to include Nyquist
>>> plt.plot(points.real, points.imag, '.')
>>> plt.gca().add_patch(plt.Circle((0,0), radius=1, fill=False, alpha=.3))
>>> plt.axis('equal'); plt.axis([-1.05, 1.05, -0.05, 1.05])
>>> plt.show()

С правильным радиусом это преобразует затухающую синусоиду (и другие с той же скоростью затухания) без спектрального просачивания:

>>> z_vals = czt(x, M + 1, w, a)  # Include Nyquist for comparison to rfft
>>> freqs = np.angle(points)*fs/(2*np.pi)  # angle = omega, radius = sigma
>>> plt.plot(freqs, abs(z_vals))
>>> plt.margins(0, 0.1)
>>> plt.show()