scipy.signal.

CZT#

класс scipy.signal.CZT(n, m=None, w=None, a=1 + 0j)[источник]#

Создать вызываемую функцию z-преобразования чирпа.

Преобразование для вычисления частотной характеристики вокруг спирали. Объекты этого класса являются вызываемыми и могут вычислять чирп-Z-преобразование на своих входных данных. Этот объект предварительно вычисляет постоянные чирпы, используемые в данном преобразовании.

Параметры:

nint: Размер сигнала.
mint, необязательный: Желаемое количество выходных точек. По умолчанию n.
wcomplex, опционально: Соотношение между точками на каждом шаге. Это должно быть точно, иначе накопленная ошибка ухудшит хвост выходной последовательности. По умолчанию равноудаленные точки по всей единичной окружности.
acomplex, опционально: Начальная точка в комплексной плоскости. По умолчанию 1+0j.

Методы

`__call__`(x, *[, axis])	Вычислить чирп Z-преобразование сигнала.
`points`()	Вернуть точки, в которых вычисляется z-преобразование чирпа.

Возвращает:

fCZT: Вызываемый объект f(x, axis=-1) для вычисления чирп z-преобразования на x.

Смотрите также

czt: Удобная функция для быстрого вычисления CZT.
ZoomFFT: Класс, создающий вызываемую функцию частичного БПФ.

Примечания

Значения по умолчанию выбраны так, чтобы f(x) эквивалентно fft.fft(x) и, если m > len(x), что f(x, m) эквивалентно fft.fft(x, m).

Если w не лежит на единичной окружности, то преобразование будет происходить по спирали с экспоненциально растущим радиусом. В любом случае, угол будет увеличиваться линейно.

Для преобразований, которые лежат на единичной окружности, точность лучше при использовании ZoomFFT, поскольку любая численная ошибка в w накапливается для длинных данных, уходя от единичной окружности.

Преобразование чирпа может быть быстрее, чем эквивалентное БПФ с дополнением нулями. Попробуйте с вашими размерами массивов, чтобы увидеть.

Однако, z-преобразование чирпа значительно менее точно, чем эквивалентное дополненное нулями БПФ.

Поскольку эта CZT реализована с использованием алгоритма Блюстейна, она может вычислять преобразования Фурье большой простой длины за время O(N log N), а не за время O(N**2), требуемое прямым вычислением DFT. (scipy.fft также использует алгоритм Блюстейна.)

(Название "chirp z-transform" происходит от использования чирпа в алгоритме Блюстейна. Он не разлагает сигналы на чирпы, как другие преобразования с "chirp" в названии.)

Ссылки

[1]

Leo I. Bluestein, «A linear filtering approach to the computation of the discrete Fourier transform,» Northeast Electronics Research and Engineering Meeting Record 10, 218-219 (1968).

[2]

Рабинер, Шафер и Радер, «Алгоритм z-преобразования чирпа и его применение», Bell Syst. Tech. J. 48, 1249-1292 (1969).

Примеры

Вычисление нескольких FFT с простой длиной:

>>> from scipy.signal import CZT
>>> import numpy as np
>>> a = np.random.rand(7)
>>> b = np.random.rand(7)
>>> c = np.random.rand(7)
>>> czt_7 = CZT(n=7)
>>> A = czt_7(a)
>>> B = czt_7(b)
>>> C = czt_7(c)

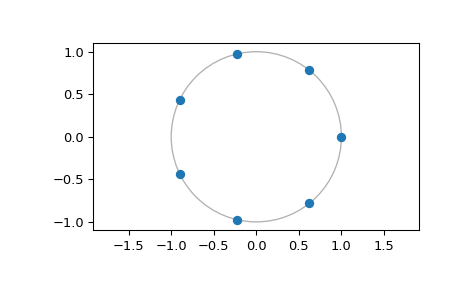
Отобразить точки, в которых вычисляется БПФ:

>>> czt_7.points()
array([ 1.00000000+0.j        ,  0.62348980+0.78183148j,
       -0.22252093+0.97492791j, -0.90096887+0.43388374j,
       -0.90096887-0.43388374j, -0.22252093-0.97492791j,
        0.62348980-0.78183148j])
>>> import matplotlib.pyplot as plt
>>> plt.plot(czt_7.points().real, czt_7.points().imag, 'o')
>>> plt.gca().add_patch(plt.Circle((0,0), radius=1, fill=False, alpha=.3))
>>> plt.axis('equal')
>>> plt.show()