scipy.signal.

zoom_fft#

scipy.signal.zoom_fft(x, fn, m=None, *, fs=2, конечная точка=False, ось=-1)[источник]#

Вычислить ДПФ от x только для частот в диапазоне fn.

Параметры:

xмассив: Сигнал для преобразования.
fnarray_like: Последовательность длины 2 [f1, f2] задающий диапазон частот, или скаляр, для которого диапазон [0, fn] предполагается.
mint, необязательный: Количество точек для вычисления. По умолчанию равно длине x.
fsfloat, опционально: Частота дискретизации. Если fs=10 представляла 10 кГц, например, тогда f1 и f2 также будет задана в кГц. Частота дискретизации по умолчанию равна 2, поэтому f1 и f2 должен быть в диапазоне [0, 1], чтобы сохранить преобразование ниже частоты Найквиста.
конечная точкаbool, необязательно: Если True, f2 Jacques Gaudin +
осьint, необязательный: Ось, по которой вычисляется БПФ. Если не задана, используется последняя ось.

Возвращает:

выходndarray: Преобразованный сигнал. Преобразование Фурье будет вычислено в точках f1, f1+df, f1+2df, …, f2, где df=(f2-f1)/m.

Смотрите также

ZoomFFT: Класс, создающий вызываемую функцию частичного БПФ.

Примечания

Значения по умолчанию выбраны так, чтобы signal.zoom_fft(x, 2) эквивалентно fft.fft(x) и, если m > len(x), что signal.zoom_fft(x, 2, m) эквивалентно fft.fft(x, m).

Для построения графика величины результирующего преобразования используйте:

plot(linspace(f1, f2, m, endpoint=False), abs(zoom_fft(x, [f1, f2], m)))

Если преобразование нужно повторить, используйте ZoomFFT для построения специализированной функции преобразования, которую можно повторно использовать без перевычисления констант.

Примеры

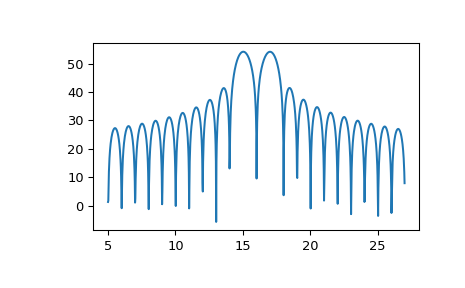
Для построения графика результатов преобразования используйте что-то вроде следующего:

>>> import numpy as np
>>> from scipy.signal import zoom_fft
>>> t = np.linspace(0, 1, 1021)
>>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t)
>>> f1, f2 = 5, 27
>>> X = zoom_fft(x, [f1, f2], len(x), fs=1021)
>>> f = np.linspace(f1, f2, len(x))
>>> import matplotlib.pyplot as plt
>>> plt.plot(f, 20*np.log10(np.abs(X)))
>>> plt.show()

../../_images/scipy-signal-zoom_fft-1.png