scipy.integrate.

cumulative_simpson#

scipy.integrate.cumulative_simpson(y, *, x=None, dx=1.0, ось=-1, начальный=None)[источник]#

Кумулятивно интегрировать y(x) с использованием составного правила Симпсона 1/3. Интеграл отсчётов в каждой точке вычисляется, предполагая квадратичную зависимость между каждой точкой и двумя соседними точками.

Параметры:

yarray_like: Значения для интегрирования. Требуется хотя бы одна точка вдоль ось. Если предоставлены две или менее точек вдоль ось, интегрирование по Симпсону невозможно, и результат вычисляется с помощью cumulative_trapezoid.
xarray_like, необязательный: Координата для интегрирования. Должна иметь ту же форму, что и y или должен быть 1D с той же длиной, что и y вдоль ось. x также должен быть строго возрастающим вдоль ось. Если x равно None (по умолчанию), интегрирование выполняется с использованием интервалов dx между последовательными элементами в y.
dxскаляр или array_like, опционально: Расстояние между элементами yИспользуется только если x равно None. Может быть либо числом с плавающей точкой, либо массивом той же формы, что и y, но длиной один вдоль ось. По умолчанию 1.0.
осьint, необязательный: Задает ось для интегрирования. По умолчанию -1 (последняя ось).
начальныйскаляр или array_like, опционально: Если задано, вставьте это значение в начало возвращаемого результата и добавьте его к остальной части результата. По умолчанию None, что означает отсутствие значения в x[0] возвращается и res имеет на один элемент меньше, чем y вдоль оси интегрирования. Может быть либо числом с плавающей точкой, либо массивом с той же формой, что и y, но длиной один вдоль ось.

Возвращает:

resndarray: Результат кумулятивного интегрирования y вдоль ось. Если начальный если None, форма такова, что ось интегрирования имеет на одно значение меньше, чем y. Если начальный задано, форма равна той же, что и y.

Смотрите также

numpy.cumsum
cumulative_trapezoid: кумулятивное интегрирование с использованием составного правила трапеций
simpson: интегратор для дискретных данных с использованием составного правила Симпсона

Примечания

Добавлено в версии 1.12.0.

Составной метод Симпсона 1/3 может использоваться для приближённого вычисления определённого интеграла от дискретизированной входной функции \(y(x)\) [1]Метод предполагает квадратичную зависимость на интервале, содержащем любые три последовательные точки выборки.

Рассмотрим три последовательные точки: \((x_1, y_1), (x_2, y_2), (x_3, y_3)\).

Предполагая квадратичную зависимость по трём точкам, интеграл по подынтервалу между \(x_1\) и \(x_2\) задаётся формулой (8) из [2]:

\[\begin{split}\int_{x_1}^{x_2} y(x) dx\ &= \frac{x_2-x_1}{6}\left[\ \left\{3-\frac{x_2-x_1}{x_3-x_1}\right\} y_1 + \ \left\{3 + \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} + \ \frac{x_2-x_1}{x_3-x_1}\right\} y_2\\ - \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} y_3\right]\end{split}\]

Интеграл между \(x_2\) и \(x_3\) задается путем замены вхождений \(x_1\) и \(x_3\). Интеграл оценивается отдельно для каждого подынтервала, а затем суммируется кумулятивно для получения окончательного результата.

Для равноотстоящих выборок результат является точным, если функция является полиномом третьей степени или ниже [1] и количество подынтервалов чётное. В противном случае интеграл точен для полиномов степени два или ниже.

Ссылки

[1] (1,2)

Страница Википедии: https://en.wikipedia.org/wiki/Simpson’s_rule

[2]

Cartwright, Kenneth V. Simpson’s Rule Cumulative Integration with MS Excel and Irregularly-spaced Data. Journal of Mathematical Sciences and Mathematics Education. 12 (2): 1-9

Примеры

>>> from scipy import integrate
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-2, 2, num=20)
>>> y = x**2
>>> y_int = integrate.cumulative_simpson(y, x=x, initial=0)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y_int, 'ro', x, x**3/3 - (x[0])**3/3, 'b-')
>>> ax.grid()
>>> plt.show()

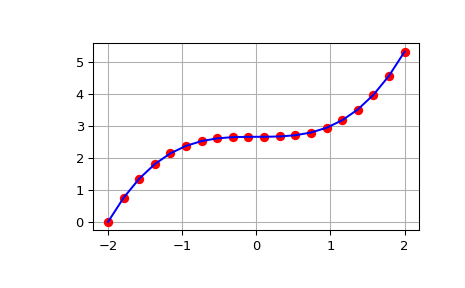
../../_images/scipy-integrate-cumulative_simpson-1_00_00.png

Вывод cumulative_simpson аналогично итеративному вызову simpson с последовательно увеличивающимися верхними пределами интегрирования, но не идентичными.

>>> def cumulative_simpson_reference(y, x):
...     return np.asarray([integrate.simpson(y[:i], x=x[:i])
...                        for i in range(2, len(y) + 1)])
>>>
>>> rng = np.random.default_rng()
>>> x, y = rng.random(size=(2, 10))
>>> x.sort()
>>>
>>> res = integrate.cumulative_simpson(y, x=x)
>>> ref = cumulative_simpson_reference(y, x)
>>> equal = np.abs(res - ref) < 1e-15
>>> equal  # not equal when `simpson` has even number of subintervals
array([False,  True, False,  True, False,  True, False,  True,  True])

Это ожидаемо: потому что cumulative_simpson имеет доступ к большему количеству информации, чем simpson, обычно может давать более точные оценки исходного интеграла по подынтервалам.