scipy.interpolate.

BarycentricInterpolator#

класс scipy.interpolate.BarycentricInterpolator(xi, yi=None, ось=0, *, wi=None, rng=None, random_state=None)[источник]#

Барицентрический интерполятор (Лагранжа с улучшенной стабильностью) (гладкость C∞).

Строит полином, проходящий через заданный набор точек. Позволяет вычислять полином и все его производные, эффективно изменять интерполируемые y-значения и обновлять, добавляя больше x- и y-значений. Для численной устойчивости используется барицентрическое представление вместо непосредственного вычисления коэффициентов полинома.

Параметры:

xiarray_like, shape (npoints, )

1-D массив x-координат точек, через которые должен проходить полином

yiarray_like, форма (…, npoints, …), необязательно

N-мерный массив y-координат точек, через которые должен проходить полином. Если None, значения y будут предоставлены позже через set_y метода. Длина yi вдоль оси интерполяции должна быть равна длине xi. Используйте axis параметр для выбора правильной оси.

осьint, необязательный

Ось в массиве yi, соответствующая значениям координаты x. По умолчанию axis=0.

wiarray_like, необязательный

Барицентрические веса для выбранных точек интерполяции xi. Если отсутствует или None, веса будут вычислены из xi (по умолчанию). Это позволяет повторно использовать веса wi если несколько интерполянтов вычисляются с использованием одних и тех же узлов xi, без перевычисления. Это также позволяет явно вычислять веса для некоторых вариантов xi (см. примечания).

rng{None, int, numpy.random.Generator, опционально

Если rng передается по ключевому слову, типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator. Если rng уже является Generator экземпляр, то предоставленный экземпляр используется. Укажите rng для воспроизводимой интерполяции.

Если этот аргумент random_state передается по ключевому слову, устаревшее поведение для аргумента random_state применяется:

Если random_state равно None (или numpy.random), numpy.random.RandomState используется синглтон.
Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state.
Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator это ключевое слово было изменено с random_state to rng. В течение переходного периода оба ключевых слова будут продолжать работать (укажите только одно из них). После переходного периода использование random_state ключевое слово будет выдавать предупреждения. Поведение random_state и rng ключевые слова описаны выше.

Атрибуты:

dtype

Методы

`__call__`(x)	Вычислить интерполяционный полином в точках x
`add_xi`(xi[, yi])	Добавьте больше значений x в набор для интерполяции
`derivative`(x[, der])	Вычислить одну производную полинома в точке x.
`derivatives`(x[, der])	Вычислить несколько производных полинома в точке x
`set_yi`(yi[, axis])	Обновить значения y для интерполяции

Примечания

Этот метод является вариантом интерполяции полиномами Лагранжа [1] на основе [2]. Вместо использования формулы Лагранжа или Ньютона, полином представлен барицентрической формулой

\[p(x) = \frac{\sum_{i=1}^m\ w_i y_i / (x - x_i)}{\sum_{i=1}^m w_i / (x - x_i)},\]

где \(w_i\) являются барицентрическими весами, вычисленными по общей формуле

\[w_i = \left( \prod_{k \neq i} x_i - x_k \right)^{-1}.\]

Это та же барицентрическая форма, используемая AAA и FloaterHormannInterpolator. Однако, в отличие от этого, веса \(w_i\) определены так, что \(p(x)\) является полиномом, а не рациональной функцией.

Барицентрическое представление позволяет избежать многих проблем, связанных с интерполяцией полиномов, вызванных арифметикой с плавающей запятой. Однако оно не позволяет избежать проблем, присущих интерполяции полиномов. А именно, если координаты x распределены равномерно, то веса могут быть вычислены явно с использованием формулы из [2]

\[w_i = (-1)^i {n \choose i},\]

где \(n\) это количество x-координат. Как отмечено в [2], это означает, что для больших \(n\) веса изменяются экспоненциально большими коэффициентами, что приводит к явлению Рунге.

Чтобы избежать этой плохой обусловленности, x-координаты должны быть сгруппированы на концах интервала. Отличный выбор точек на интервале \([a,b]\) являются точками Чебышёва второго рода

\[x_i = \frac{a + b}{2} + \frac{a - b}{2}\cos(i\pi/n).\]

в этом случае веса могут быть вычислены явно как

\[\begin{split}w_i = \begin{cases} (-1)^i/2 & i = 0,n \\ (-1)^i & \text{otherwise} \end{cases}.\end{split}\]

См. [2] для дополнительной информации. Обратите внимание, что для больших \(n\), вычисление весов явно (см. примеры) будет быстрее, чем общая формула.

Ссылки

[1]

https://en.wikipedia.org/wiki/Lagrange_polynomial

[2] (1,2,3,4)

Жан-Поль Берру и Ллойд Н. Трефетен, “Барицентрическая интерполяция Лагранжа”, SIAM Review 2004 46:3, 501-517 DOI:10.1137/S0036144502417715

Примеры

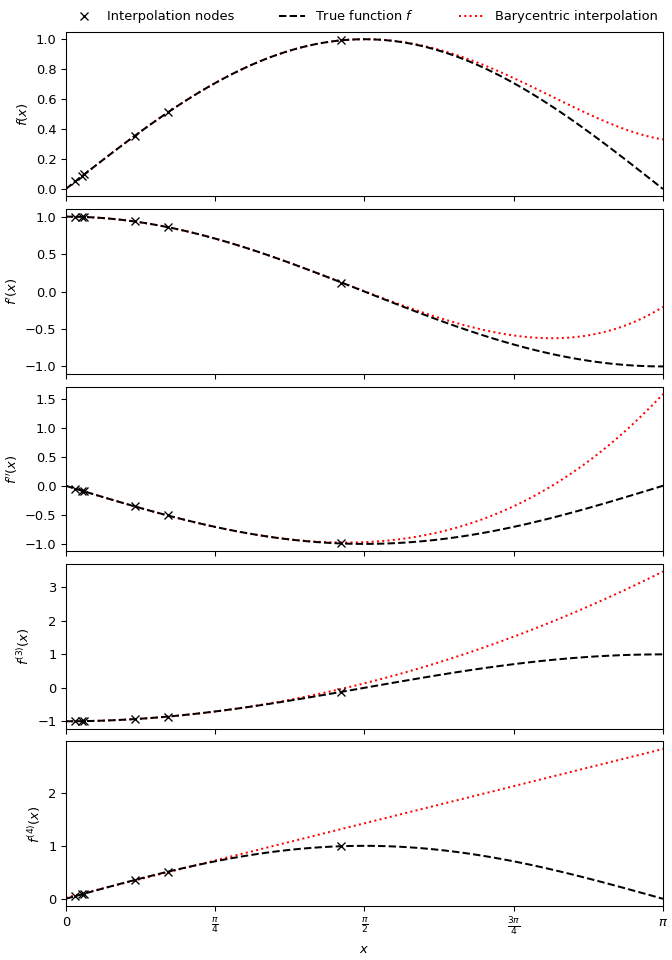
Для создания квинтического барицентрического интерполянта, аппроксимирующего функцию \(\sin x\), и его первые четыре производные, используя шесть случайно расположенных узлов в \((0, \pi/2)\):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import BarycentricInterpolator
>>> rng = np.random.default_rng()
>>> xi = rng.random(6) * np.pi/2
>>> f, f_d1, f_d2, f_d3, f_d4 = np.sin, np.cos, lambda x: -np.sin(x), lambda x: -np.cos(x), np.sin
>>> P = BarycentricInterpolator(xi, f(xi), random_state=rng)
>>> fig, axs = plt.subplots(5, 1, sharex=True, layout='constrained', figsize=(7,10))
>>> x = np.linspace(0, np.pi, 100)
>>> axs[0].plot(x, P(x), 'r:', x, f(x), 'k--', xi, f(xi), 'xk')
>>> axs[1].plot(x, P.derivative(x), 'r:', x, f_d1(x), 'k--', xi, f_d1(xi), 'xk')
>>> axs[2].plot(x, P.derivative(x, 2), 'r:', x, f_d2(x), 'k--', xi, f_d2(xi), 'xk')
>>> axs[3].plot(x, P.derivative(x, 3), 'r:', x, f_d3(x), 'k--', xi, f_d3(xi), 'xk')
>>> axs[4].plot(x, P.derivative(x, 4), 'r:', x, f_d4(x), 'k--', xi, f_d4(xi), 'xk')
>>> axs[0].set_xlim(0, np.pi)
>>> axs[4].set_xlabel(r"$x$")
>>> axs[4].set_xticks([i * np.pi / 4 for i in range(5)],
...                   ["0", r"$\frac{\pi}{4}$", r"$\frac{\pi}{2}$", r"$\frac{3\pi}{4}$", r"$\pi$"])
>>> for ax, label in zip(axs, ("$f(x)$", "$f'(x)$", "$f''(x)$", "$f^{(3)}(x)$", "$f^{(4)}(x)$")):
...     ax.set_ylabel(label)
>>> labels = ['Interpolation nodes', 'True function $f$', 'Barycentric interpolation']
>>> axs[0].legend(axs[0].get_lines()[::-1], labels, bbox_to_anchor=(0., 1.02, 1., .102),
...               loc='lower left', ncols=3, mode="expand", borderaxespad=0., frameon=False)
>>> plt.show()

../../_images/scipy-interpolate-BarycentricInterpolator-1_00_00.png

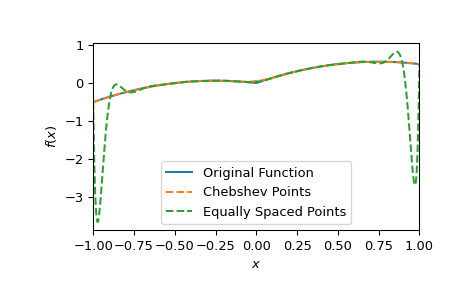
Далее мы покажем, как использование точек Чебышёва второго рода позволяет избежать явления Рунге. В этом примере мы также явно вычисляем веса.

>>> n = 20
>>> def f(x): return np.abs(x) + 0.5*x - x**2
>>> i = np.arange(n)
>>> x_cheb = np.cos(i*np.pi/(n - 1))  # Chebyshev points on [-1, 1]
>>> w_i_cheb = (-1.)**i  # Explicit formula for weights of Chebyshev points
>>> w_i_cheb[[0, -1]] /= 2
>>> p_cheb = BarycentricInterpolator(x_cheb, f(x_cheb), wi=w_i_cheb)
>>> x_equi = np.linspace(-1, 1, n)
>>> p_equi = BarycentricInterpolator(x_equi, f(x_equi))
>>> xx = np.linspace(-1, 1, 1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(xx, f(xx), label="Original Function")
>>> ax.plot(xx, p_cheb(xx), "--", label="Chebshev Points")
>>> ax.plot(xx, p_equi(xx), "--", label="Equally Spaced Points")
>>> ax.set(xlabel="$x$", ylabel="$f(x)$", xlim=[-1, 1])
>>> ax.legend()
>>> plt.show()

../../_images/scipy-interpolate-BarycentricInterpolator-1_01_00.png