scipy.interpolate.

FloaterHormannInterpolator

класс scipy.interpolate.FloaterHormannInterpolator(точки, values, *, d=3)

Барицентрический рациональный интерполятор Флотера-Хорманна (C∞ гладкий на вещественной оси).

Как описано в [1], метод Флоатера и Хорманна вычисляет веса для барицентрического рационального интерполянта без полюсов на вещественной оси.

Параметры:

x1D array_like, форма (n,)

Одномерный массив, содержащий значения независимой переменной. Значения могут быть вещественными или комплексными, но должны быть конечными.

yarray_like, форма (n, …)

Массив, содержащий значения зависимой переменной. Бесконечные и NaN значения y и соответствующие значения x будет отброшен.

dint, по умолчанию: 3

Целое число, удовлетворяющее 0 <= d < n. Интерполяция Флотера-Хорманна смешивает n - d многочлены степени d вместе; для d = n - 1, это эквивалентно полиномиальной интерполяции.

Атрибуты:

весамассив

Веса барицентрической аппроксимации.

Методы

__call__(z)	Вычислить рациональную аппроксимацию при заданных значениях.
poles()	Вычислить полюсы рациональной аппроксимации.
residues()	Вычислить вычеты полюсов аппроксимации.
roots()	Вычислить нули рациональной аппроксимации.

Смотрите также

AAA

Барицентрическая рациональная аппроксимация вещественных и комплексных функций.

pade

Аппроксимация Паде.

Примечания

Интерполянт Флотера-Хорманна — это рациональная функция, которая интерполирует данные с порядком аппроксимации \(O(h^{d+1})\). Рациональная функция смешивает n - d многочлены степени d вместе для создания рационального интерполянта, который не содержит полюсов на вещественной оси, в отличие от AAA. Интерполянт задаётся формулой

\[r(x) = \frac{\sum_{i=0}^{n-d} \lambda_i(x) p_i(x)} {\sum_{i=0}^{n-d} \lambda_i(x)},\]

где \(p_i(x)\) является интерполяционным полиномом степени не выше d через точки \((x_i,y_i),\dots,(x_{i+d},y_{i+d})\), и \(\lambda_i(z)\) являются функциями смешивания, определенными

\[\lambda_i(x) = \frac{(-1)^i}{(x - x_i)\cdots(x - x_{i+d})}.\]

Когда d = n - 1 это сводится к полиномиальной интерполяции.

Благодаря своей стабильности, для вычислений используется следующее барицентрическое представление приведенного выше уравнения

\[r(z) = \frac{\sum_{k=1}^m\ w_k f_k / (x - x_k)}{\sum_{k=1}^m w_k / (x - x_k)},\]

где веса \(w_j\) вычисляются как

\[\begin{split}w_k &= (-1)^{k - d} \sum_{i \in J_k} \prod_{j = i, j \neq k}^{i + d} 1/|x_k - x_j|, \\ J_k &= \{ i \in I: k - d \leq i \leq k\},\\ I &= \{0, 1, \dots, n - d\}.\end{split}\]

Ссылки

[1]

M.S. Floater и K. Hormann, «Барицентрическая рациональная интерполяция без полюсов и с высокой скоростью аппроксимации», Numer. Math. 107, 315 (2007). DOI:10.1007/s00211-007-0093-y

Примеры

Попробуйте в вашем браузере!

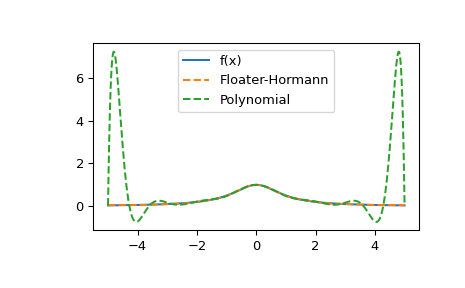
Здесь мы сравниваем метод с полиномиальной интерполяцией на примере, где полиномиальная интерполяция терпит неудачу из-за явления Рунге.

>>> import numpy as np
>>> from scipy.interpolate import (FloaterHormannInterpolator,
...                                BarycentricInterpolator)
>>> def f(x):
...     return 1/(1 + x**2)
>>> x = np.linspace(-5, 5, num=15)
>>> r = FloaterHormannInterpolator(x, f(x))
>>> p = BarycentricInterpolator(x, f(x))
>>> xx = np.linspace(-5, 5, num=1000)
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.plot(xx, f(xx), label="f(x)")
>>> ax.plot(xx, r(xx), "--", label="Floater-Hormann")
>>> ax.plot(xx, p(xx), "--", label="Polynomial")
>>> ax.legend()
>>> plt.show()

НазадОткрыть во вкладке