scipy.interpolate.

RegularGridInterpolator#

класс scipy.interpolate.RegularGridInterpolator(точки, values, метод='linear', bounds_error=True, fill_value=nan, *, solver=None, solver_args=None)[источник]#

Интерполятор указанного порядка на прямоугольной сетке в N ≥ 1 измерений.

Данные должны быть определены на прямоугольной сетке; то есть на прямоугольной сетке с равномерным или неравномерным шагом. Поддерживаются линейная, ближайшего соседа и сплайновая интерполяции. После настройки объекта-интерполятора метод интерполяции может быть выбран при каждом вычислении.

Параметры:

точкикортеж ndarray из чисел с плавающей запятой, с формами (m1, ), …, (mn, ): Точки, определяющие регулярную сетку в n измерениях. Точки в каждом измерении (т.е. каждый элемент кортежа points) должны быть строго возрастающими или убывающими.
valuesarray_like, shape (m1, …, mn, …): Данные на регулярной сетке в n измерениях. Принимаются комплексные данные.
методstr, optional: Метод интерполяции для выполнения. Поддерживаются "linear", "nearest", "slinear", "cubic", "quintic" и "pchip". Этот параметр станет значением по умолчанию для объекта __call__ метод. По умолчанию — "linear".
bounds_errorbool, необязательно: Если True, при запросе интерполированных значений вне области входных данных возникает ValueError. Если False, то fill_value используется. По умолчанию True.
fill_valuefloat или None, опционально: Значение для использования в точках вне области интерполяции. Если None, значения вне области экстраполируются. По умолчанию np.nan.
solverвызываемый объект, необязательный: Используется только для методов "slinear", "cubic" и "quintic". Разреженный решатель линейной алгебры для построения экземпляра NdBSpline. По умолчанию используется итеративный решатель scipy.sparse.linalg.gcrotmk.

Добавлено в версии 1.13.
solver_args: dict, optional: Дополнительные аргументы для передачи в solver, если есть.

Добавлено в версии 1.13.

Атрибуты:

сеткакортеж ndarrays: Точки, определяющие регулярную сетку в n измерениях. Этот кортеж определяет полную сетку через np.meshgrid(*grid, indexing='ij')
valuesndarray: Значения данных на сетке.
методstr: Метод интерполяции.
fill_valuefloat или None: Используйте это значение для аргументов вне границ в __call__.
bounds_errorbool: Если True, аргумент вне границ вызывает ValueError.

Методы

__call__(xi[, method, nu])

Интерполяция по координатам.

Смотрите также

NearestNDInterpolator: Интерполятор ближайшего соседа на неструктурированный данные в N измерениях
LinearNDInterpolator: Кусочно-линейный интерполятор на неструктурированный данные в N измерениях
interpn: удобная функция, которая оборачивает RegularGridInterpolator
scipy.ndimage.map_coordinates: интерполяция на сетках с равным шагом (подходит, например, для передискретизации N-мерных изображений)

Примечания

В отличие от LinearNDInterpolator и NearestNDInterpolator, этот класс избегает дорогостоящей триангуляции входных данных, используя преимущества структуры регулярной сетки.

Другими словами, этот класс предполагает, что данные определены на прямолинейный сетка.

Добавлено в версии 0.14.

Методы 'slinear'(k=1), 'cubic'(k=3) и 'quintic'(k=5) являются интерполяторами сплайнов тензорного произведения, где k является степенью сплайна, Если любое измерение имеет меньше точек, чем k + 1, будет вызвана ошибка.

Добавлено в версии 1.9.

Если входные данные таковы, что размерности имеют несоизмеримые единицы измерения и отличаются на много порядков величины, интерполянт может иметь числовые артефакты. Рассмотрите возможность масштабирования данных перед интерполяцией.

Выбор решателя для методов сплайнов

Методы сплайнов, «slinear», «cubic» и «quintic», включают решение большой разреженной линейной системы во время инициализации. В зависимости от данных стандартный решатель может быть или не быть адекватным. Если он не подходит, может потребоваться экспериментировать с опциональным solver аргумент, где вы можете выбрать между прямым решателем (scipy.sparse.linalg.spsolve) или итерационные решатели из scipy.sparse.linalg. Возможно, вам потребуется предоставить дополнительные параметры через необязательный solver_args параметр (например, вы можете предоставить начальное значение или целевую погрешность). См. scipy.sparse.linalg документация для полного списка доступных опций.

В качестве альтернативы вы можете использовать устаревшие методы "slinear_legacy", "cubic_legacy" и "quintic_legacy". Эти методы позволяют более быстрое построение, но вычисления будут значительно медленнее.

Правило округления в половинных точках с методом `nearest`

Правило округления с ближайший метод в половинных точках округляет вниз.

Ссылки

[1]

Пакет Python regulargrid Йоханнеса Бюхнера, см. https://pypi.python.org/pypi/regulargrid/

[2]

Википедия, "Trilinear interpolation", https://en.wikipedia.org/wiki/Trilinear_interpolation

[3]

Вайзер, Алан и Серхио Э. Заратонтелло. «Заметка о кусочно-линейной и мультилинейной табличной интерполяции во многих измерениях». MATH. COMPUT. 50.181 (1988): 189-196. https://www.ams.org/journals/mcom/1988-50-181/S0025-5718-1988-0917826-0/S0025-5718-1988-0917826-0.pdf DOI:10.1090/S0025-5718-1988-0917826-0

Примеры

Вычислить функцию в точках 3-D сетки

В качестве первого примера мы вычисляем простую примерную функцию в точках трехмерной сетки:

>>> from scipy.interpolate import RegularGridInterpolator
>>> import numpy as np
>>> def f(x, y, z):
...     return 2 * x**3 + 3 * y**2 - z
>>> x = np.linspace(1, 4, 11)
>>> y = np.linspace(4, 7, 22)
>>> z = np.linspace(7, 9, 33)
>>> xg, yg ,zg = np.meshgrid(x, y, z, indexing='ij', sparse=True)
>>> data = f(xg, yg, zg)

data теперь является 3-D массивом с data[i, j, k] = f(x[i], y[j], z[k]). Затем определите интерполирующую функцию из этих данных:

>>> interp = RegularGridInterpolator((x, y, z), data)

Вычислить интерполирующую функцию в двух точках (x,y,z) = (2.1, 6.2, 8.3) и (3.3, 5.2, 7.1):

>>> pts = np.array([[2.1, 6.2, 8.3],
...                 [3.3, 5.2, 7.1]])
>>> interp(pts)
array([ 125.80469388,  146.30069388])

что действительно является близким приближением к

>>> f(2.1, 6.2, 8.3), f(3.3, 5.2, 7.1)
(125.54200000000002, 145.894)

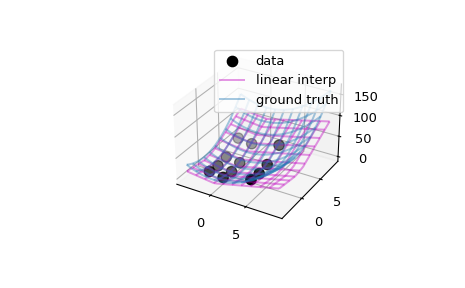
Интерполировать и экстраполировать 2D набор данных

В качестве второго примера мы интерполируем и экстраполируем двумерный набор данных:

>>> x, y = np.array([-2, 0, 4]), np.array([-2, 0, 2, 5])
>>> def ff(x, y):
...     return x**2 + y**2

>>> xg, yg = np.meshgrid(x, y, indexing='ij')
>>> data = ff(xg, yg)
>>> interp = RegularGridInterpolator((x, y), data,
...                                  bounds_error=False, fill_value=None)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> ax.scatter(xg.ravel(), yg.ravel(), data.ravel(),
...            s=60, c='k', label='data')

Оценить и построить интерполятор на более мелкой сетке

>>> xx = np.linspace(-4, 9, 31)
>>> yy = np.linspace(-4, 9, 31)
>>> X, Y = np.meshgrid(xx, yy, indexing='ij')

>>> # interpolator
>>> ax.plot_wireframe(X, Y, interp((X, Y)), rstride=3, cstride=3,
...                   alpha=0.4, color='m', label='linear interp')

>>> # ground truth
>>> ax.plot_wireframe(X, Y, ff(X, Y), rstride=3, cstride=3,
...                   alpha=0.4, label='ground truth')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-interpolate-RegularGridInterpolator-1_00_00.png

Другие примеры приведены в учебнике.