scipy.interpolate.

griddata#

scipy.interpolate.griddata(точки, values, xi, метод='linear', fill_value=nan, масштабировать=False)[источник]#

Удобная функция для интерполяции неструктурированных данных в нескольких измерениях.

Параметры:

точки2-D ndarray чисел с плавающей точкой формы (n, D), или кортеж длины D из 1-D ndarray формы (n,).

Координаты точек данных.

valuesndarray из float или complex, форма (n,)

Значения данных.

xi2-D ndarray чисел с плавающей точкой формы (m, D) или кортеж длины D из ndarrays, транслируемых к той же форме.

Точки, в которых интерполируются данные.

метод{‘linear’, ‘nearest’, ‘cubic’}, опционально

Метод интерполяции. Один из

nearest: возвращает значение в точке данных, ближайшей к точке интерполяции. См. NearestNDInterpolator для более подробной информации.
linear: Разбить входное множество точек на N-мерные симплексы и выполнить линейную интерполяцию на каждом симплексе. См. LinearNDInterpolator для получения дополнительной информации.
cubic (1-D): вернуть значение, определенное из кубического сплайна.
cubic (2-D): возвращает значение, определённое кусочно-кубической, непрерывно дифференцируемой (C1) и приблизительно минимизирующей кривизну полиномиальной поверхности. См. CloughTocher2DInterpolator для получения дополнительной информации.

fill_valuefloat, опционально

Значение, используемое для заполнения запрошенных точек вне выпуклой оболочки входных точек. Если не указано, то по умолчанию nan. Эта опция не влияет на метод 'nearest'.

масштабироватьbool, необязательно

Масштабировать точки до единичного куба перед выполнением интерполяции. Это полезно, если некоторые из входных измерений имеют несоизмеримые единицы и различаются на много порядков величины.

Добавлено в версии 0.14.0.

Возвращает:

ndarray: Массив интерполированных значений.

Смотрите также

LinearNDInterpolator: Кусочно-линейный интерполятор в N измерениях.
NearestNDInterpolator: Интерполятор ближайшего соседа в N измерениях.
CloughTocher2DInterpolator: Кусочно-кубический, C1-гладкий, минимизирующий кривизну интерполятор в 2D.
interpn: Интерполяция на регулярной или прямоугольной сетке.
RegularGridInterpolator: Интерполятор на регулярной или прямоугольной сетке в произвольных размерностях (interpn оборачивает этот класс).

Примечания

Добавлено в версии 0.9.

Примечание

Для данных на регулярной сетке используйте interpn вместо этого.

Примеры

Предположим, мы хотим интерполировать 2-D функцию

>>> import numpy as np
>>> def func(x, y):
...     return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

на сетке в [0, 1]x[0, 1]

>>> grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]

но мы знаем его значения только в 1000 точках данных:

>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])

Это можно сделать с помощью griddata – ниже мы пробуем все методы интерполяции:

>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

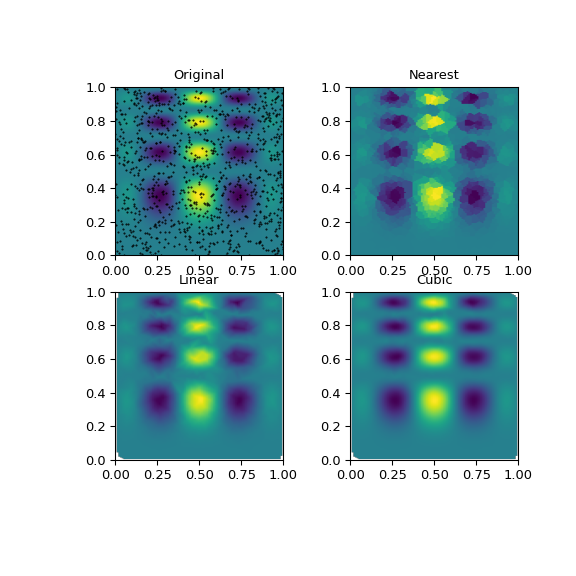
Можно видеть, что точный результат воспроизводится всеми методами в некоторой степени, но для этой гладкой функции кусочно-кубический интерполянт дает наилучшие результаты:

>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
>>> plt.plot(points[:,0], points[:,1], 'k.', ms=1)
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()

../../_images/scipy-interpolate-griddata-1.png