scipy.interpolate.

RectSphereBivariateSpline#

класс scipy.interpolate.RectSphereBivariateSpline(u, v, r, s=0.0, pole_continuity=False, pole_values=None, pole_exact=False, pole_flat=False)[источник]#

Бивариативная сплайн-аппроксимация по прямоугольной сетке на сфере.

Может использоваться для сглаживания данных.

Добавлено в версии 0.11.0.

Параметры:

uarray_like: Одномерный массив координат широты в строго возрастающем порядке. Координаты должны быть заданы в радианах и лежать в открытом интервале (0, pi).
varray_like: Одномерный массив координат долготы в строго возрастающем порядке. Координаты должны быть заданы в радианах. Первый элемент (v[0]) должен лежать в интервале [-pi, pi). Последний элемент (v[-1]) должно удовлетворять v[-1] <= v[0] + 2*pi.
rarray_like: 2-мерный массив данных с формой (u.size, v.size).
sfloat, опционально: Положительный коэффициент сглаживания, определённый для условия оценки (s=0 предназначен для интерполяции).
pole_continuitybool или (bool, bool), опционально: Порядок непрерывности на полюсах u=0 (pole_continuity[0]) и u=pi (pole_continuity[1]). Порядок непрерывности на полюсе будет 1 или 0, когда это True или False, соответственно. По умолчанию False.
pole_valuesfloat или (float, float), опционально: Значения данных на полюсах u=0 и u=pi. Либо весь параметр, либо каждый отдельный элемент может быть None. По умолчанию None.
pole_exactbool или (bool, bool), опционально: Точность значений данных на полюсах u=0 и u=pi. Если True, значение считается правым значением функции и будет точно аппроксимировано. Если False, значение будет считаться данными, как и другие значения данных. По умолчанию False.
pole_flatbool или (bool, bool), опционально: Для полюсов в u=0 и u=pi, укажите, имеет ли аппроксимация исчезающие производные. По умолчанию False.

Методы

`__call__`(theta, phi[, dtheta, dphi, grid])	Вычисление сплайна или его производных в заданных позициях.
`ev`(theta, phi[, dtheta, dphi])	Вычислить сплайн в точках
`get_coeffs`()	Вернуть коэффициенты сплайна.
`get_knots`()	Возвращает кортеж (tx,ty), где tx,ty содержат позиции узлов сплайна относительно переменных x и y соответственно.
`get_residual`()	Возвращает взвешенную сумму квадратов невязок аппроксимации сплайном: sum ((w[i](z[i]-s(x[i],y[i])))*2,axis=0)
`partial_derivative`(dx, dy)	Построить новый сплайн, представляющий частную производную этого сплайна.

Смотрите также

BivariateSpline: базовый класс для двумерных сплайнов.
UnivariateSpline: гладкий одномерный сплайн для аппроксимации заданного набора точек данных.
SmoothBivariateSpline: сглаживающий двумерный сплайн через заданные точки
LSQBivariateSpline: двумерный сплайн с использованием взвешенного метода наименьших квадратов
SmoothSphereBivariateSpline: сглаживающий двумерный сплайн в сферических координатах
LSQSphereBivariateSpline: двумерный сплайн в сферических координатах с использованием взвешенного метода наименьших квадратов
RectBivariateSpline: двумерный сплайн на прямоугольной сетке.
bisplrep: функция для нахождения бивариантного B-сплайнового представления поверхности
bisplev: функция для вычисления двумерного B-сплайна и его производных

Примечания

В настоящее время только аппроксимация сглаживающим сплайном (iopt[0] = 0 и iopt[0] = 1 в процедуре FITPACK) поддерживается. Точная аппроксимация сплайнами методом наименьших квадратов ещё не реализована.

При фактическом выполнении интерполяции запрошенные v значения должны лежать в том же интервале длины 2pi, что и исходные v значения были выбраны из.

Для получения дополнительной информации см. FITPACK сайт об этой функции.

Примеры

Предположим, у нас есть глобальные данные на грубой сетке

>>> import numpy as np
>>> lats = np.linspace(10, 170, 9) * np.pi / 180.
>>> lons = np.linspace(0, 350, 18) * np.pi / 180.
>>> data = np.dot(np.atleast_2d(90. - np.linspace(-80., 80., 18)).T,
...               np.atleast_2d(180. - np.abs(np.linspace(0., 350., 9)))).T

Мы хотим интерполировать его на глобальную сетку с разрешением один градус

>>> new_lats = np.linspace(1, 180, 180) * np.pi / 180
>>> new_lons = np.linspace(1, 360, 360) * np.pi / 180
>>> new_lats, new_lons = np.meshgrid(new_lats, new_lons)

Нам нужно настроить объект интерполятора

>>> from scipy.interpolate import RectSphereBivariateSpline
>>> lut = RectSphereBivariateSpline(lats, lons, data)

Наконец мы интерполируем данные. RectSphereBivariateSpline объект принимает только одномерные массивы на вход, поэтому необходимо выполнить преобразование формы.

>>> data_interp = lut.ev(new_lats.ravel(),
...                      new_lons.ravel()).reshape((360, 180)).T

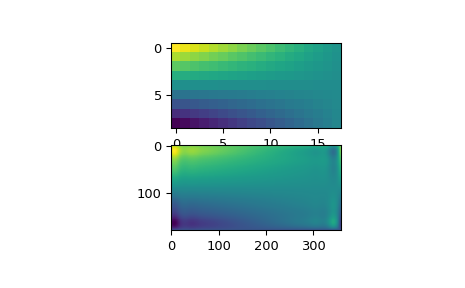
Глядя на исходные и интерполированные данные, можно увидеть, что интерполянт очень хорошо воспроизводит исходные данные:

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> ax1.imshow(data, interpolation='nearest')
>>> ax2 = fig.add_subplot(212)
>>> ax2.imshow(data_interp, interpolation='nearest')
>>> plt.show()

../../_images/scipy-interpolate-RectSphereBivariateSpline-1_00_00.png

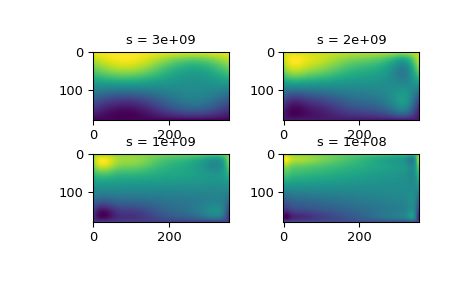
Выбор оптимального значения s может быть деликатной задачей. Рекомендуемые значения для s зависят от точности значений данных. Если пользователь имеет представление о статистических ошибках в данных, она также может найти правильную оценку для s. Предполагая, что, если она укажет правильный s, интерполятор будет использовать сплайн f(u,v) которая точно воспроизводит функцию, лежащую в основе данных, она может вычислить sum((r(i,j)-s(u(i),v(j)))**2) чтобы найти хорошую оценку для этого s. Например, если она знает, что статистические ошибки в её r(i,j)-значения не больше 0.1, она может ожидать, что хороший s должно иметь значение не больше, чем u.size * v.size * (0.1)**2.

Если ничего не известно о статистической ошибке в r(i,j), s должен быть определён методом проб и ошибок. Лучше всего начать с очень большого значения s (для определения полинома наименьших квадратов и соответствующей верхней границы fp0 для s) и затем постепенно уменьшать значение s (например, в 10 раз в начале, т.е. s = fp0 / 10, fp0 / 100, ... и более тщательно (по мере того как приближение показывает больше деталей) для получения более точных соответствий.

Результаты интерполяции для различных значений s дать некоторое представление об этом процессе:

>>> fig2 = plt.figure()
>>> s = [3e9, 2e9, 1e9, 1e8]
>>> for idx, sval in enumerate(s, 1):
...     lut = RectSphereBivariateSpline(lats, lons, data, s=sval)
...     data_interp = lut.ev(new_lats.ravel(),
...                          new_lons.ravel()).reshape((360, 180)).T
...     ax = fig2.add_subplot(2, 2, idx)
...     ax.imshow(data_interp, interpolation='nearest')
...     ax.set_title(f"s = {sval:g}")
>>> plt.show()

../../_images/scipy-interpolate-RectSphereBivariateSpline-1_01_00.png