scipy.interpolate.

SmoothSphereBivariateSpline

класс scipy.interpolate.SmoothSphereBivariateSpline(theta, phi, r, w=None, s=0.0, eps=1e-16)

Сглаженная бивариативная сплайн-аппроксимация в сферических координатах.

Добавлено в версии 0.11.0.

Параметры:

theta, phi, rarray_like

1-D последовательности точек данных (порядок не важен). Координаты должны быть заданы в радианах. Тета должна лежать в интервале [0, pi], и phi должен лежать в интервале [0, 2pi].

warray_like, необязательный

Положительная 1-D последовательность весов.

sfloat, опционально

Положительный коэффициент сглаживания, определенный для условия оценки: sum((w(i)*(r(i) - s(theta(i), phi(i))))**2, axis=0) <= s По умолчанию s=len(w) что должно быть хорошим значением, если 1/w[i] является оценкой стандартного отклонения r[i].

epsfloat, опционально

Порог для определения эффективного ранга переопределённой системы линейных уравнений. eps должно иметь значение в открытом интервале (0, 1), по умолчанию равно 1e-16.

Методы

__call__(theta, phi[, dtheta, dphi, grid])	Вычисление сплайна или его производных в заданных позициях.
ev(theta, phi[, dtheta, dphi])	Вычислить сплайн в точках
get_coeffs()	Вернуть коэффициенты сплайна.
get_knots()	Возвращает кортеж (tx,ty), где tx,ty содержат позиции узлов сплайна относительно переменных x и y соответственно.
get_residual()	Возвращает взвешенную сумму квадратов невязок аппроксимации сплайном: sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0)
partial_derivative(dx, dy)	Построить новый сплайн, представляющий частную производную этого сплайна.

Смотрите также

BivariateSpline

базовый класс для двумерных сплайнов.

UnivariateSpline

гладкий одномерный сплайн для аппроксимации заданного набора точек данных.

SmoothBivariateSpline

сглаживающий двумерный сплайн через заданные точки

LSQBivariateSpline

двумерный сплайн с использованием взвешенного метода наименьших квадратов

RectSphereBivariateSpline

двумерный сплайн по прямоугольной сетке на сфере

LSQSphereBivariateSpline

двумерный сплайн в сферических координатах с использованием взвешенного метода наименьших квадратов

RectBivariateSpline

двумерный сплайн на прямоугольной сетке.

bisplrep

функция для нахождения бивариантного B-сплайнового представления поверхности

bisplev

функция для вычисления двумерного B-сплайна и его производных

Примечания

Для получения дополнительной информации см. FITPACK сайт об этой функции.

Примеры

Попробуйте в вашем браузере!

Предположим, у нас есть глобальные данные на грубой сетке (входные данные не обязательно должны быть на сетке):

>>> import numpy as np
>>> theta = np.linspace(0., np.pi, 7)
>>> phi = np.linspace(0., 2*np.pi, 9)
>>> data = np.empty((theta.shape[0], phi.shape[0]))
>>> data[:,0], data[0,:], data[-1,:] = 0., 0., 0.
>>> data[1:-1,1], data[1:-1,-1] = 1., 1.
>>> data[1,1:-1], data[-2,1:-1] = 1., 1.
>>> data[2:-2,2], data[2:-2,-2] = 2., 2.
>>> data[2,2:-2], data[-3,2:-2] = 2., 2.
>>> data[3,3:-2] = 3.
>>> data = np.roll(data, 4, 1)

Нам нужно настроить объект интерполятора

>>> lats, lons = np.meshgrid(theta, phi)
>>> from scipy.interpolate import SmoothSphereBivariateSpline
>>> lut = SmoothSphereBivariateSpline(lats.ravel(), lons.ravel(),
...                                   data.T.ravel(), s=3.5)

В качестве первого теста посмотрим, что возвращает алгоритм при запуске на входных координатах

>>> data_orig = lut(theta, phi)

Наконец, мы интерполируем данные на более мелкую сетку

>>> fine_lats = np.linspace(0., np.pi, 70)
>>> fine_lons = np.linspace(0., 2 * np.pi, 90)

>>> data_smth = lut(fine_lats, fine_lons)

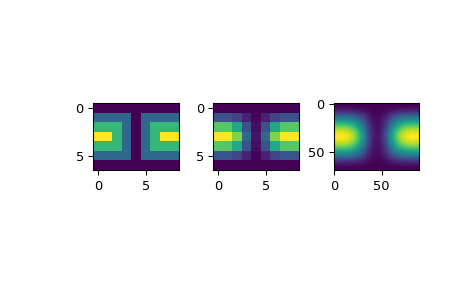
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(131)
>>> ax1.imshow(data, interpolation='nearest')
>>> ax2 = fig.add_subplot(132)
>>> ax2.imshow(data_orig, interpolation='nearest')
>>> ax3 = fig.add_subplot(133)
>>> ax3.imshow(data_smth, interpolation='nearest')
>>> plt.show()

НазадОткрыть во вкладке