scipy.interpolate.

UnivariateSpline#

класс scipy.interpolate.UnivariateSpline(x, y, w=None, ограничивающая рамка=[None, None, k=3, s=None, расширение=0, check_finite=False)[источник]#

Сглаживающий сплайн 1-D, аппроксимирующий заданный набор точек данных.

Наследие

Этот класс считается устаревшим и больше не будет получать обновления. Хотя в настоящее время у нас нет планов по его удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. В частности, мы рекомендуем использовать make_splrep вместо этого.

Аппроксимирует сплайн y = spl(x) степени k к предоставленному x, y data. s задаёт количество узлов, указывая условие сглаживания.

Параметры:

x(N,) array_like

Одномерный массив независимых входных данных. Должен быть возрастающим; должен быть строго возрастающим, если s равен 0.

y(N,) array_like

Одномерный массив зависимых входных данных той же длины, что и x.

w(N,) array_like, optional

Веса для подгонки сплайна. Должны быть положительными. Если w равно None, веса все равны 1. По умолчанию None.

ограничивающая рамка(2,) array_like, необязательный

2-последовательность, задающая границы интервала аппроксимации. Если ограничивающая рамка равно None, bbox=[x[0], x[-1]]. По умолчанию None.

kint, необязательный

Степень сглаживающего сплайна. Должна быть 1 <= k <= 5. k = 3 является кубическим сплайном. По умолчанию 3.

sfloat или None, опционально

Положительный коэффициент сглаживания, используемый для выбора количества узлов. Количество узлов будет увеличиваться до тех пор, пока не будет выполнено условие сглаживания:

sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s

Однако из-за численных проблем фактическое условие:

abs(sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) - s) < 0.001 * s

Если s равно None, s будет установлен как len(w) для сглаживающего сплайна, который использует все точки данных. Если 0, сплайн будет интерполировать через все точки данных. Это эквивалентно InterpolatedUnivariateSpline. По умолчанию None. Пользователь может использовать s для управления компромиссом между близостью и гладкостью аппроксимации. Большие s означает большее сглаживание, тогда как меньшие значения s указывают на меньшее сглаживание. Рекомендуемые значения s зависят от весов, w. Если веса представляют обратное стандартное отклонение y, тогда хороший s значение должно находиться в диапазоне (m-sqrt(2*m),m+sqrt(2*m)) где m — количество точек данных в x, y, и w. Это означает s = len(w) должно быть хорошим значением, если 1/w[i] является оценкой стандартного отклонения y[i].

расширениеint или str, необязательно

Управляет режимом экстраполяции для элементов, не находящихся в интервале, определенном последовательностью узлов.

если ext=0 или 'extrapolate', вернуть экстраполированное значение.
если ext=1 или ‘zeros’, вернуть 0
если ext=2 или ‘raise’, вызвать ValueError
если ext=3 или ‘const’, вернуть граничное значение.

По умолчанию 0.

check_finitebool, необязательно

Проверять ли, что входные массивы содержат только конечные числа. Отключение может повысить производительность, но может привести к проблемам (сбоям, бесконечному выполнению или бессмысленным результатам), если входные данные содержат бесконечности или NaN. По умолчанию: False.

Методы

`__call__`(x[, nu, ext])	Вычислить сплайн (или его nu-ю производную) в позициях x.
`antiderivative`([n])	Создайте новый сплайн, представляющий первообразную этого сплайна.
`derivative`([n])	Создать новый сплайн, представляющий производную этого сплайна.
`derivatives`(x)	Вернуть все производные сплайна в точке x.
`get_coeffs`()	Вернуть коэффициенты сплайна.
`get_knots`()	Возвращает позиции внутренних узлов сплайна.
`get_residual`()	Вернуть взвешенную сумму квадратов остатков аппроксимации сплайном.
`integral`(a, b)	Возвращает определенный интеграл сплайна между двумя заданными точками.
`roots`()	Возвращает нули сплайна.
`set_smoothing_factor`(s)	Продолжить вычисление сплайна с заданным коэффициентом сглаживания s и узлами, найденными при последнем вызове.

validate_input

Смотрите также

BivariateSpline: базовый класс для двумерных сплайнов.
SmoothBivariateSpline: сглаживающий двумерный сплайн через заданные точки
LSQBivariateSpline: двумерный сплайн с использованием взвешенного метода наименьших квадратов
RectSphereBivariateSpline: двумерный сплайн по прямоугольной сетке на сфере
SmoothSphereBivariateSpline: сглаживающий двумерный сплайн в сферических координатах
LSQSphereBivariateSpline: двумерный сплайн в сферических координатах с использованием взвешенного метода наименьших квадратов
RectBivariateSpline: двумерный сплайн на прямоугольной сетке
InterpolatedUnivariateSpline: Интерполирующий одномерный сплайн для заданного набора точек данных.
bisplrep: функция для нахождения бивариантного B-сплайнового представления поверхности
bisplev: функция для вычисления двумерного B-сплайна и его производных
splrep: функция для нахождения B-сплайнового представления 1-D кривой
splev: функция для оценки B-сплайна или его производных
sproot: функция для нахождения корней кубического B-сплайна
splint: функция для вычисления определённого интеграла B-сплайна между двумя заданными точками
spalde: функция для вычисления всех производных B-сплайна

Примечания

Количество точек данных должно быть больше степени сплайна k.

обработка NaN: Если входные массивы содержат nan значения, результат не полезен, поскольку базовые процедуры подгонки сплайнов не могут работать с nan. Обходным решением является использование нулевых весов для точек данных, не являющихся числами:

>>> import numpy as np
>>> from scipy.interpolate import UnivariateSpline
>>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4])
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> spl = UnivariateSpline(x, y, w=~w)

Обратите внимание на необходимость замены nan числовым значением (точное значение не имеет значения, пока соответствующий вес равен нулю.)

Ссылки

На основе алгоритмов, описанных в [1], [2], [3], и [4]:

[1]

P. Dierckx, «Алгоритм сглаживания, дифференцирования и интегрирования экспериментальных данных с использованием сплайн-функций», J.Comp.Appl.Maths 1 (1975) 165-184.

[2]

P. Dierckx, "A fast algorithm for smoothing data on a rectangular grid while using spline functions", SIAM J.Numer.Anal. 19 (1982) 1286-1304.

[3]

П. Диеркс, «Улучшенный алгоритм аппроксимации кривых сплайн-функциями», отчет tw54, кафедра компьютерных наук, К.У. Лёвен, 1981.

[4]

P. Dierckx, «Curve and surface fitting with splines», Monographs on Numerical Analysis, Oxford University Press, 1993.

Примеры

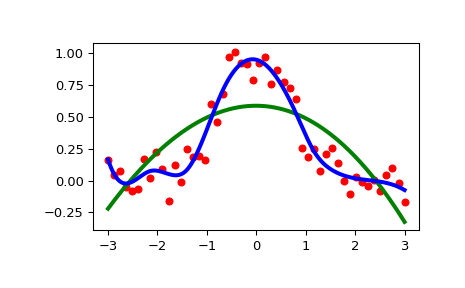
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import UnivariateSpline
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
>>> plt.plot(x, y, 'ro', ms=5)

Используйте значение по умолчанию для параметра сглаживания:

>>> spl = UnivariateSpline(x, y)
>>> xs = np.linspace(-3, 3, 1000)
>>> plt.plot(xs, spl(xs), 'g', lw=3)

Вручную изменить степень сглаживания:

>>> spl.set_smoothing_factor(0.5)
>>> plt.plot(xs, spl(xs), 'b', lw=3)
>>> plt.show()

../../_images/scipy-interpolate-UnivariateSpline-1.png