scipy.interpolate.

approximate_taylor_polynomial

scipy.interpolate.approximate_taylor_polynomial(f, x, степень, scale, порядок=None)

Оценить полином Тейлора f в x с помощью подгонки полинома.

Параметры:

fcallable

Функция, для которой ищется полином Тейлора. Должна принимать вектор из x значения.

xскаляр

Точка, в которой полином должен быть вычислен.

степеньint

Степень полинома Тейлора

scaleскаляр

Ширина интервала для оценки полинома Тейлора. Значения функции, распределённые по такому диапазону, используются для подгонки полинома. Должна быть выбрана тщательно.

порядокint или None, опционально

Порядок полинома, используемого при подгонке; f будет вычислено order+1 раз. Если None, использовать степень.

Возвращает:

pэкземпляр poly1d

Полином Тейлора (сдвинутый к началу координат, так что например p(0)=f(x)).

Примечания

Правильный выбор «масштаба» — это компромисс; слишком большой, и функция слишком сильно отличается от своего полинома Тейлора, чтобы получить хороший ответ, слишком маленький, и ошибки округления подавляют члены высшего порядка. Используемый алгоритм становится численно неустойчивым около порядка 30 даже в идеальных условиях.

Выбор порядка несколько большего, чем степень, может улучшить члены высшего порядка.

Примеры

Попробуйте в вашем браузере!

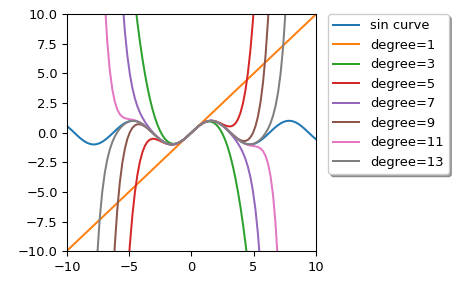
Мы можем вычислить полиномы аппроксимации Тейлора для функции sin с различными степенями:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import approximate_taylor_polynomial
>>> x = np.linspace(-10.0, 10.0, num=100)
>>> plt.plot(x, np.sin(x), label="sin curve")
>>> for degree in np.arange(1, 15, step=2):
...     sin_taylor = approximate_taylor_polynomial(np.sin, 0, degree, 1,
...                                                order=degree + 2)
...     plt.plot(x, sin_taylor(x), label=f"degree={degree}")
>>> plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left',
...            borderaxespad=0.0, shadow=True)
>>> plt.tight_layout()
>>> plt.axis([-10, 10, -10, 10])
>>> plt.show()

НазадОткрыть во вкладке