scipy.interpolate.

lagrange#

scipy.interpolate.lagrange(x, w)[источник]#

Возвращает интерполяционный полином Лагранжа.

Даны два одномерных массива x и w, возвращает интерполяционный полином Лагранжа через точки (x, w).

Предупреждение: Эта реализация численно неустойчива. Не ожидайте возможности использовать более чем около 20 точек, даже если они выбраны оптимально.

Параметры:

xarray_like: x представляет x-координаты набора точек данных.
warray_like: w представляет y-координаты набора точек данных, т.е., f(x).

Возвращает:

lagrangenumpy.poly1d экземпляр: Интерполяционный полином Лагранжа.

Примечания

Название этой функции относится к тому факту, что возвращаемый объект представляет полином Лагранжа - единственный полином наименьшей степени, который интерполирует заданный набор данных [1]. Он вычисляет полином по формуле разделённых разностей Ньютона [2]; то есть он работает с полиномами Ньютона, а не с полиномами Лагранжа. Для численных расчётов барицентрическая форма интерполяции Лагранжа (scipy.interpolate.BarycentricInterpolator) обычно более подходит.

Ссылки

[1]

Серое закрытие состоит в последовательности серого расширения и серого сужения. Википедия. https://en.wikipedia.org/wiki/Lagrange_polynomial

[2]

Полином Ньютона. Википедия. https://en.wikipedia.org/wiki/Newton_polynomial

Примеры

Интерполировать \(f(x) = x^3\) по 3 точкам.

>>> import numpy as np
>>> from scipy.interpolate import lagrange
>>> x = np.array([0, 1, 2])
>>> y = x**3
>>> poly = lagrange(x, y)

Поскольку есть только 3 точки, полином Лагранжа имеет степень 2. Явно он задается формулой

\[\begin{split}\begin{aligned} L(x) &= 1\times \frac{x (x - 2)}{-1} + 8\times \frac{x (x-1)}{2} \\ &= x (-2 + 3x) \end{aligned}\end{split}\]

>>> from numpy.polynomial.polynomial import Polynomial
>>> Polynomial(poly.coef[::-1]).coef
array([ 0., -2.,  3.])

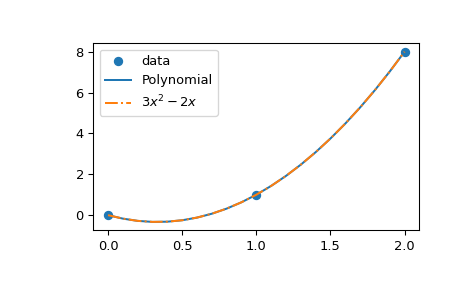
>>> import matplotlib.pyplot as plt
>>> x_new = np.arange(0, 2.1, 0.1)
>>> plt.scatter(x, y, label='data')
>>> plt.plot(x_new, Polynomial(poly.coef[::-1])(x_new), label='Polynomial')
>>> plt.plot(x_new, 3*x_new**2 - 2*x_new + 0*x_new,
...          label=r"$3 x^2 - 2 x$", linestyle='-.')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-interpolate-lagrange-1.png