scipy.interpolate.

make_smoothing_spline#

scipy.interpolate.make_smoothing_spline(x, y, w=None, lam=None, *, ось=0)[источник]#

Создать сглаживающий B-сплайн, удовлетворяющий критерию обобщённой перекрёстной проверки (GCV).

Вычислить (коэффициенты) функции сглаживающего кубического сплайна, используя lam для управления компромиссом между степенью гладкости кривой и её близостью к данным. В случае lam равно None, используется критерий GCV [1] для его нахождения.

Сглаживающий сплайн находится как решение регуляризованной взвешенной задачи линейной регрессии:

\[\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2 + \lambda\int\limits_{x_1}^{x_n} (f^{(2)}(u))^2 d u\]

где \(f\) является сплайн-функцией, \(w\) является вектором весов и \(\lambda\) является параметром регуляризации.

Если lam равно None, мы используем критерий GCV для поиска оптимального параметра регуляризации, в противном случае мы решаем взвешенную линейную регрессионную задачу с заданным параметром. Параметр контролирует компромисс следующим образом: чем больше становится параметр, тем более гладкой становится функция.

Параметры:

xarray_like, форма (n,): Абсциссы. n должно быть не менее 5.
yarray_like, форма (n, …): Ординаты. n должно быть не менее 5.
warray_like, shape (n,), optional: Вектор весов. По умолчанию np.ones_like(x).
lamfloat, (\(\lambda \geq 0\)), optional: Параметр регуляризации. Если lam равно None, тогда оно находится из критерия GCV. По умолчанию None.
осьint, необязательный: Ось данных. По умолчанию ноль. Предполагается, что y.shape[axis] == n, и все остальные оси y являются осями пакетной обработки.

Возвращает:

функцияBSpline object: Объект, представляющий сплайн в базисе B-сплайнов как решение задачи сглаживающих сплайнов с использованием критерия GCV [1] в случае lam is None, в противном случае используется заданный параметр lam.

Примечания

Этот алгоритм является чистой переработкой алгоритма, представленного Вольтрингом на FORTRAN [2]. Оригинальная версия не может быть использована в исходном коде SciPy из-за проблем с лицензией. Детали переработки обсуждаются здесь (доступно только на русском) [4].

Если вектор весов w равен None, мы предполагаем, что все точки равны по весам, и вектор весов является вектором единиц.

Обратите внимание, что во взвешенной сумме квадратов остатков веса не возводятся в квадрат: \(\sum\limits_{i=1}^n w_i\lvert y_i - f(x_i) \rvert^2\) в то время как в splrep сумма строится из квадратов весов.

В случаях, когда исходная задача плохо обусловлена (например, произведение \(X^T W X\) где \(X\) является матрицей плана, не является положительно определенной матрицей) возникает ValueError.

Ссылки

[1]

Г. Вабба, «Оценка параметра сглаживания» в Spline models for observational data, Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1990, стр. 45-65. DOI:10.1137/1.9781611970128

[2]

H. J. Woltring, A Fortran package for generalized, cross-validatory spline smoothing and differentiation, Advances in Engineering Software, vol. 8, no. 2, pp. 104-113, 1986. DOI:10.1016/0141-1195(86)90098-7

[3]

Т. Хасти, Дж. Фридман и Р. Тибширани, «Сглаживающие сплайны» в Элементы статистического обучения: интеллектуальный анализ данных, вывод и прогнозирование, Нью-Йорк: Springer, 2017, стр. 241-249. DOI:10.1007/978-0-387-84858-7

[4]

E. Земляной, «Обобщенные сглаживающие сплайны с перекрестной проверкой», дипломная работа бакалавра, 2022. https://www.hse.ru/ba/am/students/diplomas/620910604 (на русском)

Примеры

Сгенерируйте некоторые зашумленные данные

>>> import numpy as np
>>> np.random.seed(1234)
>>> n = 200
>>> def func(x):
...    return x**3 + x**2 * np.sin(4 * x)
>>> x = np.sort(np.random.random_sample(n) * 4 - 2)
>>> y = func(x) + np.random.normal(scale=1.5, size=n)

Создать функцию сглаживающего сплайна

>>> from scipy.interpolate import make_smoothing_spline
>>> spl = make_smoothing_spline(x, y)

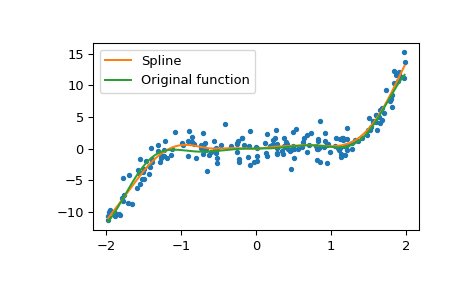
Построить график обоих

>>> import matplotlib.pyplot as plt
>>> grid = np.linspace(x[0], x[-1], 400)
>>> plt.plot(x, y, '.')
>>> plt.plot(grid, spl(grid), label='Spline')
>>> plt.plot(grid, func(grid), label='Original function')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-make_smoothing_spline-1.png