scipy.interpolate.

make_lsq_spline#

scipy.interpolate.make_lsq_spline(x, y, t, k=3, w=None, ось=0, check_finite=True, *, метод='qr')[источник]#

Создать сглаживающий B-сплайн, удовлетворяющий критерию наименьших квадратов (LSQ).

Результат представляет собой линейную комбинацию

\[S(x) = \sum_j c_j B_j(x; t)\]

базисных элементов B-сплайна, \(B_j(x; t)\), который минимизирует

\[\sum_{j} \left( w_j \times (S(x_j) - y_j) \right)^2\]

Параметры:

xarray_like, shape (m,): Абсциссы.
yarray_like, shape (m, …): Ординаты.
tarray_like, форма (n + k + 1,).: Узлы. Узлы и точки данных должны удовлетворять условиям Шёнберга-Уитни.
kint, необязательный: Степень B-сплайна. По умолчанию кубическая, k = 3.
warray_like, shape (m,), optional: Веса для сплайн-аппроксимации. Должны быть положительными. Если None, тогда все веса равны. По умолчанию None.
осьint, необязательный: Ось интерполяции. По умолчанию равна нулю.
check_finitebool, необязательно: Проверять ли, что входные массивы содержат только конечные числа. Отключение может повысить производительность, но может привести к проблемам (сбоям, незавершению), если входные данные содержат бесконечности или NaN. По умолчанию True.
методstr, optional: Метод решения линейной задачи наименьших квадратов. Допустимые значения: "norm-eq" (явное построение и решение нормальной системы уравнений) и "qr" (использование QR-факторизации матрицы плана). По умолчанию "qr".

Возвращает:

bBSpline object: A BSpline объект степени k с узлами t.

Смотрите также

BSpline: базовый класс, представляющий объекты B-сплайнов
make_interp_spline: аналогичная фабричная функция для интерполяционных сплайнов
LSQUnivariateSpline: процедура подгонки сплайна на основе FITPACK
splrep: подпрограмма подгонки на основе FITPACK

Примечания

Количество точек данных должно быть больше степени сплайна k.

Узлы t должны удовлетворять условиям Шёнберга-Уитни, т.е. должно существовать подмножество точек данных x[j] такой, что t[j] < x[j] < t[j+k+1], для j=0, 1,...,n-k-2.

Примеры

Сгенерировать некоторые зашумленные данные:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)

Теперь подгоним сглаживающий кубический сплайн с предопределёнными внутренними узлами. Здесь мы делаем вектор узлов (k+1)-регулярным, добавляя граничные узлы:

>>> from scipy.interpolate import make_lsq_spline, BSpline
>>> t = [-1, 0, 1]
>>> k = 3
>>> t = np.r_[(x[0],)*(k+1),
...           t,
...           (x[-1],)*(k+1)]
>>> spl = make_lsq_spline(x, y, t, k)

Для сравнения мы также построим интерполяционный сплайн для того же набора данных:

>>> from scipy.interpolate import make_interp_spline
>>> spl_i = make_interp_spline(x, y)

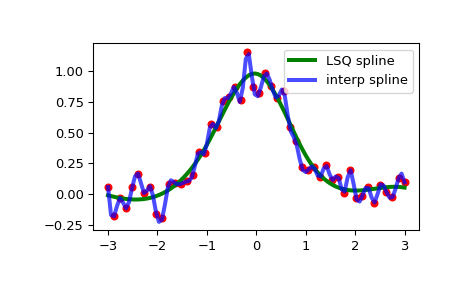
Построить оба графика:

>>> xs = np.linspace(-3, 3, 100)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3, label='LSQ spline')
>>> plt.plot(xs, spl_i(xs), 'b-', lw=3, alpha=0.7, label='interp spline')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-make_lsq_spline-1_00_00.png

обработка NaN: Если входные массивы содержат nan значения, результат не полезен, поскольку базовые процедуры подгонки сплайнов не могут работать с nan. Обходным решением является использование нулевых весов для точек данных, не являющихся числами:

>>> y[8] = np.nan
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> tck = make_lsq_spline(x, y, t, w=~w)

Обратите внимание на необходимость замены nan числовым значением (точное значение не имеет значения, пока соответствующий вес равен нулю.)