scipy.optimize.

least_squares

scipy.optimize.least_squares(fun, x0, jac='2-point', границы=(-inf, inf), метод='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=None, потеря='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options=None, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs=None, callback=None, workers=None)

Решить задачу нелинейных наименьших квадратов с ограничениями на переменные.

Учитывая остатки f(x) (m-мерная вещественная функция от n вещественных переменных) и функцию потерь rho(s) (скалярная функция), least_squares находит локальный минимум функции стоимости F(x):

minimize F(x) = 0.5 * sum(rho(f_i(x)**2), i = 0, ..., m - 1)
subject to lb <= x <= ub

Цель функции потерь rho(s) — уменьшить влияние выбросов на решение.

Параметры:

funcallable

Функция, которая вычисляет вектор невязок, с сигнатурой fun(x, *args, **kwargs), т.е., минимизация выполняется относительно её первого аргумента. Аргумент x переданный в эту функцию является ndarray формы (n,) (никогда скаляр, даже для n=1). Он должен выделить и вернуть 1-D массивоподобный объект формы (m,) или скаляр. Если аргумент x является комплексным или функция fun возвращает комплексные невязки, он должен быть обернут в вещественную функцию вещественных аргументов, как показано в конце раздела Examples.

x0array_like с формой (n,) или float

Начальное приближение для независимых переменных. Если задано число с плавающей точкой, оно будет обработано как одномерный массив с одним элементом. Когда метод равно 'trf', начальное предположение может быть немного скорректировано, чтобы лежать достаточно внутри заданного границы.

jac{‘2-point’, ‘3-point’, ‘cs’, callable}, optional

Метод вычисления матрицы Якоби (матрица размером m на n, где элемент (i, j) — частная производная f[i] по x[j]). Ключевые слова выбирают схему конечных разностей для численной оценки. Схема '3-point' более точна, но требует вдвое больше операций, чем '2-point' (по умолчанию). Схема 'cs' использует комплексные шаги и, хотя потенциально самая точная, применима только когда fun корректно обрабатывает комплексные входные данные и может быть аналитически продолжена на комплексную плоскость. Если вызываемый, используется как jac(x, *args, **kwargs) и должна возвращать хорошее приближение (или точное значение) для якобиана в виде array_like (применяется np.atleast_2d), разреженного массива (предпочтительно csr_array для производительности) или scipy.sparse.linalg.LinearOperator.

Изменено в версии 1.16.0: Структурирующий элемент, используемый для операции открытия. Ненулевые элементы считаются True. Если структурирующий элемент не предоставлен, генерируется элемент с квадратной связностью, равной единице (т.е. только ближайшие соседи связаны с центром, диагонально связанные элементы не считаются соседями).

границы2-кортеж из array_like или Bounds, опционально

Есть два способа указать границы:

1. Экземпляр Bounds класс

2. Нижние и верхние границы независимых переменных. По умолчанию границы отсутствуют. Каждый массив должен соответствовать размеру x0 или быть скаляром, в последнем случае граница будет одинаковой для всех переменных. Используйте np.inf с соответствующим знаком, чтобы отключить ограничения на все или некоторые переменные.

метод{'trf', 'dogbox', 'lm'}, optional

Алгоритм для выполнения минимизации.

• ‘trf’ : Алгоритм Trust Region Reflective, особенно подходит для больших разреженных задач с ограничениями. Обычно надежный метод.

• ‘dogbox’ : алгоритм собачьей ноги с прямоугольными областями доверия, типичный случай использования — небольшие задачи с ограничениями. Не рекомендуется для задач с вырожденной матрицей Якоби.

• 'lm' : алгоритм Левенберга-Марквардта, реализованный в MINPACK. Не обрабатывает границы и разреженные матрицы Якоби. Обычно наиболее эффективный метод для небольших неограниченных задач.

По умолчанию 'trf'. См. примечания для дополнительной информации.

ftolfloat или None, опционально

Допуск для завершения по изменению функции стоимости. По умолчанию 1e-8. Процесс оптимизации останавливается, когда dF < ftol * F, и было адекватное соответствие между локальной квадратичной моделью и истинной моделью на последнем шаге.

Если None и 'method' не 'lm', завершение по этому условию отключено. Если 'method' — 'lm', этот допуск должен быть выше машинного эпсилона.

xtolfloat или None, опционально

Допуск для завершения по изменению независимых переменных. По умолчанию 1e-8. Точное условие зависит от метод использовано:

• Для 'trf' и 'dogbox': norm(dx) < xtol * (xtol + norm(x)).

• Для 'lm' : Delta < xtol * norm(xs), где Delta является радиусом доверительной области и xs является значением x масштабируется в соответствии с x_scale параметр (см. ниже).

Если None и 'method' не 'lm', завершение по этому условию отключено. Если 'method' — 'lm', этот допуск должен быть выше машинного эпсилона.

gtolfloat или None, опционально

Допуск для завершения по норме градиента. По умолчанию 1e-8. Точное условие зависит от метод использовано:

• Для 'trf': norm(g_scaled, ord=np.inf) < gtol, где g_scaled — это значение градиента, масштабированное с учетом наличия границ [STIR].

• Для 'dogbox' : norm(g_free, ord=np.inf) < gtol, где g_free является градиентом по переменным, которые не находятся в оптимальном состоянии на границе.

• Для ‘lm’: максимальное абсолютное значение косинуса углов между столбцами матрицы Якоби и вектором невязки меньше чем gtol, или вектор невязки равен нулю.

Если None и 'method' не 'lm', завершение по этому условию отключено. Если 'method' — 'lm', этот допуск должен быть выше машинного эпсилона.

x_scale{None, array_like, 'jac'}, необязательный

Характерный масштаб каждой переменной. Установка x_scale эквивалентно переформулированию задачи в масштабированных переменных xs = x / x_scale. Альтернативный взгляд состоит в том, что размер области доверия вдоль j-го измерения пропорционален x_scale[j]. Улучшенная сходимость может быть достигнута установкой x_scale такой, что шаг заданного размера вдоль любой из масштабированных переменных имеет схожий эффект на функцию стоимости. Если установлено в ‘jac’, масштаб итеративно обновляется с использованием обратных норм столбцов матрицы Якоби (как описано в [JJMore]). Масштабирование по умолчанию для каждого метода (т.е. если x_scale is None) выглядит следующим образом:

• Для 'trf' : x_scale == 1

• Для 'dogbox' : x_scale == 1

• Для 'lm': x_scale == 'jac'

Изменено в версии 1.16.0: Значение ключевого слова по умолчанию изменено с 1 на None, чтобы указать, что используется подход по умолчанию к масштабированию. Для метода 'lm' масштабирование по умолчанию изменено с 1 на 'jac'. Было обнаружено, что это дает лучшую производительность и соответствует масштабированию, выполняемому leastsq.

потеряstr или callable, опционально

Определяет функцию потерь. Допускаются следующие значения ключевых слов:

• ‘linear’ (по умолчанию) : rho(z) = z. Даёт стандартную задачу наименьших квадратов.

• 'soft_l1' : rho(z) = 2 * ((1 + z)**0.5 - 1). Гладкая аппроксимация потерь l1 (абсолютного значения). Обычно хороший выбор для устойчивых наименьших квадратов.

• ‘huber’: rho(z) = z if z <= 1 else 2*z**0.5 - 1. Работает аналогично 'soft_l1'.

• 'cauchy' : rho(z) = ln(1 + z). Сильно ослабляет влияние выбросов, но может вызвать трудности в процессе оптимизации.

• ‘arctan’ : rho(z) = arctan(z). Ограничивает максимальные потери на одном остатке, имеет свойства, аналогичные 'cauchy'.

Если вызываемый объект, он должен принимать 1-D ndarray z=f**2 и возвращает array_like формы (3, m), где строка 0 содержит значения функции, строка 1 содержит первые производные, а строка 2 содержит вторые производные. Метод 'lm' поддерживает только 'linear' потери.

f_scalefloat, опционально

Значение мягкого отступа между остатками выбросов и невыбросов, по умолчанию равно 1.0. Функция потерь вычисляется следующим образом rho_(f**2) = C**2 * rho(f**2 / C**2), где C является f_scale, и rho определяется потеря параметр. Этот параметр не оказывает эффекта с loss='linear', но для других потеря значения это имеет решающее значение.

max_nfevNone или int, опционально

Для всех методов этот параметр контролирует максимальное количество вычислений функции, используемых каждым методом, отдельно от тех, что используются в численном приближении якобиана. Если None (по умолчанию), значение выбирается автоматически как 100 * n.

Изменено в версии 1.16.0: Значение по умолчанию для метода 'lm' изменено на 100 * n, как для вызываемого объекта, так и для численно оцененного якобиана. Ранее значение по умолчанию при использовании оцененного якобиана было 100 * n * (n + 1), потому что метод включал вычисления, используемые при оценке.

diff_stepNone или array_like, опционально

Определяет относительный размер шага для конечной разности аппроксимации якобиана. Фактический шаг вычисляется как x * diff_stepЕсли None (по умолчанию), то diff_step принимается за условно "оптимальную" степень машинного эпсилон для используемой схемы конечных разностей [NR].

tr_solver{None, 'exact', 'lsmr'}, необязательный

Метод решения подзадач доверительной области, актуален только для методов 'trf' и 'dogbox'.

• ‘exact’ подходит для не очень больших задач с плотными матрицами Якоби. Вычислительная сложность на итерацию сравнима с сингулярным разложением матрицы Якоби.

• 'lsmr' подходит для задач с разреженными и большими матрицами Якоби. Использует итеративную процедуру scipy.sparse.linalg.lsmr для нахождения решения задачи линейных наименьших квадратов и требует только вычислений матрично-векторных произведений.

Если None (по умолчанию), решатель выбирается на основе типа матрицы Якоби, возвращённой на первой итерации.

tr_optionsdict, optional

Параметры ключевых слов, передаваемые решателю доверительной области.

• tr_solver='exact': tr_options игнорируются.

• tr_solver='lsmr': опции для scipy.sparse.linalg.lsmr. Дополнительно, method='trf' поддерживает опцию ‘regularize’ (bool, по умолчанию True), которая добавляет регуляризационный член к нормальному уравнению, что улучшает сходимость, если якобиан имеет недостаточный ранг [Byrd] (уравнение 3.4).

jac_sparsity{None, array_like, sparse array}, опционально

Определяет структуру разреженности матрицы Якоби для оценки конечными разностями, её форма должна быть (m, n). Если матрица Якоби имеет только несколько ненулевых элементов в каждый строка, предоставление структуры разреженности значительно ускорит вычисления [Curtis]. Нулевой элемент означает, что соответствующий элемент в матрице Якоби тождественно равен нулю. Если предоставлено, принудительно использует решатель доверительной области 'lsmr'. Если None (по умолчанию), будет использоваться плотное дифференцирование. Не влияет на метод 'lm'.

verbose{0, 1, 2}, опционально

Уровень детализации алгоритма:

• 0 (по умолчанию) : работать без вывода сообщений.

• 1 : отобразить отчет о завершении.

• 2 : отображать прогресс во время итераций (не поддерживается методом 'lm').

args, kwargsкортеж и словарь, необязательно

Дополнительные аргументы, передаваемые в fun и jac. Оба пусты по умолчанию. Сигнатура вызова fun(x, *args, **kwargs) и то же для jac.

callbackNone или вызываемый объект, необязательно

Функция обратного вызова, вызываемая алгоритмом на каждой итерации. Может использоваться для вывода или построения результатов оптимизации на каждом шаге, а также для остановки алгоритма оптимизации на основе некоторого пользовательского условия. Реализовано только для trf и dogbox методы.

Сигнатура: callback(intermediate_result: OptimizeResult)

intermediate_result — это `scipy.optimize.OptimizeResult который содержит промежуточные результаты оптимизации на текущей итерации.

Обратный вызов также поддерживает сигнатуру вида: callback(x)

Интроспекция используется для определения того, какая из сигнатур вызывается.

Если callback функция вызывает исключение StopIteration алгоритм оптимизации остановится и вернёт статусный код -2.

Добавлено в версии 1.16.0.

workersmap-like callable, optional

Вызываемый объект, подобный отображению, такой как multiprocessing.Pool.map для параллельного вычисления любой численной производной. Это вычисление выполняется как workers(fun, iterable).

Добавлено в версии 1.16.0.

Возвращает:

результатOptimizeResult

OptimizeResult со следующими определёнными полями:

xndarray, форма (n,)

Решение найдено.

стоимостьfloat

Значение целевой функции в решении.

funndarray, форма (m,)

Вектор невязок в решении.

jacndarray, разреженный массив или LinearOperator, форма (m, n)

Модифицированная матрица Якоби в решении, в том смысле, что J^T J является приближением Гаусса-Ньютона гессиана функции стоимости. Тип такой же, как используемый алгоритмом.

gradndarray, форма (m,)

Градиент функции стоимости в решении.

оптимальностьfloat

Мера оптимальности первого порядка. В задачах без ограничений это всегда равномерная норма градиента. В задачах с ограничениями это величина, которая сравнивалась с gtol во время итераций.

active_maskndarray из int, форма (n,)

Каждый компонент показывает, активен ли соответствующий ограничение (то есть, находится ли переменная на границе):

• 0 : ограничение не активно.

• -1: активна нижняя граница.

• 1 : верхняя граница активна.

Может быть несколько произвольным для метода 'trf', так как он генерирует последовательность строго допустимых итераций и active_mask определяется в пределах порога допуска.

nfevint

Количество выполненных оценок функции. Это число не включает вызовы функций, использованные для численной аппроксимации Якобиана.

Изменено в версии 1.16.0: Для метода 'lm' количество вызовов функции, используемых в численной аппроксимации Якобиана, больше не включается. Это сделано для приведения всех методов в соответствие.

njevint или None

Количество выполненных вычислений якобиана. Если используется численная аппроксимация якобиана в методе 'lm', оно устанавливается в None.

statusint

Причина завершения алгоритма:

• -2 : завершено, потому что обратный вызов вызвал StopIteration.

• -1 : возвращен статус некорректных входных параметров из MINPACK.

• 0 : превышено максимальное количество вычислений функции.

• 1 : gtol условие завершения удовлетворено.

• 2 : ftol условие завершения удовлетворено.

• 3 : xtol условие завершения удовлетворено.

• 4 : Оба ftol и xtol условия завершения удовлетворены.

messagestr

Словесное описание причины завершения.

successbool

True, если выполнено одно из условий сходимости (status > 0).

Смотрите также

leastsq

Устаревшая обёртка для реализации MINPACK алгоритма Левенберга-Марквардта.

curve_fit

Минимизация метода наименьших квадратов, применённая к задаче аппроксимации кривой.

Примечания

Метод 'lm' (Левенберга-Марквардта) вызывает обёртку над алгоритмом наименьших квадратов, реализованным в MINPACK (lmder). Он запускает алгоритм Левенберга-Марквардта, сформулированный как алгоритм типа доверительной области. Реализация основана на статье [JJMore], она очень надёжна и эффективна с множеством умных трюков. Она должна быть вашим первым выбором для неограниченных задач. Обратите внимание, что она не поддерживает границы. Также, она не работает, когда m < n.

Метод 'trf' (Trust Region Reflective) мотивирован процессом решения системы уравнений, которые составляют условие оптимальности первого порядка для задачи минимизации с ограничениями, сформулированной в [STIR]. Алгоритм итеративно решает подзадачи доверительной области, дополненные специальным диагональным квадратичным членом и с формой доверительной области, определяемой расстоянием от границ и направлением градиента. Эти улучшения помогают избежать шагов непосредственно в границы и эффективно исследовать всё пространство переменных. Для дальнейшего улучшения сходимости алгоритм рассматривает направления поиска, отражённые от границ. Чтобы соответствовать теоретическим требованиям, алгоритм сохраняет итерации строго допустимыми. При плотных матрицах Якоби подзадачи доверительной области решаются точным методом, очень похожим на описанный в [JJMore] (и реализован в MINPACK). Отличие от реализации MINPACK заключается в том, что сингулярное разложение матрицы Якоби выполняется один раз за итерацию, вместо QR-разложения и серии исключений вращений Гивенса. Для больших разреженных матриц Якоби используется 2-D подпространственный подход решения подзадач доверительной области [STIR], [Byrd]. Подпространство натянуто на масштабированный градиент и приближённое решение Гаусса-Ньютона, предоставленное scipy.sparse.linalg.lsmrКогда не накладываются ограничения, алгоритм очень похож на MINPACK и имеет в целом сопоставимую производительность. Алгоритм работает достаточно устойчиво в неограниченных и ограниченных задачах, поэтому выбран в качестве алгоритма по умолчанию.

Метод 'dogbox' работает в рамках доверительной области, но рассматривает прямоугольные доверительные области в отличие от обычных эллипсоидов [Voglis]. Пересечение текущей области доверия и начальных границ снова является прямоугольным, поэтому на каждой итерации задача квадратичной минимизации с ограничениями в виде границ решается приближенно методом собачьей лапы Пауэлла [NumOpt]. Необходимый шаг Гаусса-Ньютона может быть вычислен точно для плотных матриц Якоби или приближённо с помощью scipy.sparse.linalg.lsmr для больших разреженных матриц Якоби. Алгоритм, вероятно, будет демонстрировать медленную сходимость, когда ранг Якоби меньше числа переменных. Алгоритм часто превосходит 'trf' в ограниченных задачах с небольшим числом переменных.

Робастные функции потерь реализованы, как описано в [BA]. Идея заключается в модификации вектора невязки и матрицы Якоби на каждой итерации таким образом, чтобы вычисленный градиент и аппроксимация гессиана по Гауссу-Ньютону соответствовали истинному градиенту и аппроксимации гессиана функции стоимости. Затем алгоритм продолжается обычным образом, т.е. устойчивые функции потерь реализованы как простая обертка над стандартными алгоритмами наименьших квадратов.

Добавлено в версии 0.17.0.

Ссылки

[STIR] (1,2,3)

M. A. Branch, T. F. Coleman, and Y. Li, "A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems," SIAM Journal on Scientific Computing, Vol. 21, Number 1, pp 1-23, 1999.

[NR]

William H. Press и др., «Numerical Recipes. The Art of Scientific Computing. 3rd edition», Sec. 5.7.

[Бёрд] (1,2)

R. H. Byrd, R. B. Schnabel и G. A. Shultz, «Приближённое решение задачи доверительной области путём минимизации по двумерным подпространствам», Math. Programming, 40, стр. 247-263, 1988.

[Curtis]

A. Curtis, M. J. D. Powell, и J. Reid, "Об оценке разреженных матриц Якоби", Journal of the Institute of Mathematics and its Applications, 13, стр. 117-120, 1974.

[JJMore] (1,2,3)

J. J. More, «The Levenberg-Marquardt Algorithm: Implementation and Theory», Numerical Analysis, под ред. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, стр. 105-116, 1977.

[Воглис]

C. Voglis и I. E. Lagaris, “A Rectangular Trust Region Dogleg Approach for Unconstrained and Bound Constrained Nonlinear Optimization”, WSEAS International Conference on Applied Mathematics, Корфу, Греция, 2004.

[NumOpt]

Дж. Ноцедал и С. Дж. Райт, "Численная оптимизация, 2-е издание", Глава 4.

[BA]

B. Triggs и др., “Bundle Adjustment - A Modern Synthesis”, Proceedings of the International Workshop on Vision Algorithms: Theory and Practice, pp. 298-372, 1999.

Примеры

Попробуйте в вашем браузере!

В этом примере мы находим минимум функции Розенброка без ограничений на независимые переменные.

>>> import numpy as np
>>> def fun_rosenbrock(x):
...     return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])

Обратите внимание, что мы предоставляем только вектор остатков. Алгоритм строит целевую функцию как сумму квадратов остатков, что дает функцию Розенброка. Точный минимум находится в x = [1.0, 1.0].

>>> from scipy.optimize import least_squares
>>> x0_rosenbrock = np.array([2, 2])
>>> res_1 = least_squares(fun_rosenbrock, x0_rosenbrock)
>>> res_1.x
array([ 1.,  1.])
>>> res_1.cost
9.8669242910846867e-30
>>> res_1.optimality
8.8928864934219529e-14

Теперь мы ограничиваем переменные таким образом, что предыдущее решение становится недопустимым. В частности, мы требуем, чтобы x[1] >= 1.5, и x[0] оставить неограниченным. Для этого мы указываем границы параметр к least_squares в форме bounds=([-np.inf, 1.5], np.inf).

Мы также предоставляем аналитический якобиан:

>>> def jac_rosenbrock(x):
...     return np.array([
...         [-20 * x[0], 10],
...         [-1, 0]])

Собирая всё вместе, мы видим, что новое решение лежит на границе:

>>> res_2 = least_squares(fun_rosenbrock, x0_rosenbrock, jac_rosenbrock,
...                       bounds=([-np.inf, 1.5], np.inf))
>>> res_2.x
array([ 1.22437075,  1.5       ])
>>> res_2.cost
0.025213093946805685
>>> res_2.optimality
1.5885401433157753e-07

Теперь решаем систему уравнений (т.е. функция стоимости должна быть равна нулю в минимуме) для бройденовской трехдиагональной векторнозначной функции от 100000 переменных:

>>> def fun_broyden(x):
...     f = (3 - x) * x + 1
...     f[1:] -= x[:-1]
...     f[:-1] -= 2 * x[1:]
...     return f

Соответствующая матрица Якоби является разреженной. Мы указываем алгоритму оценивать её с помощью конечных разностей и предоставляем структуру разреженности матрицы Якоби, чтобы значительно ускорить этот процесс.

>>> from scipy.sparse import lil_array
>>> def sparsity_broyden(n):
...     sparsity = lil_array((n, n), dtype=int)
...     i = np.arange(n)
...     sparsity[i, i] = 1
...     i = np.arange(1, n)
...     sparsity[i, i - 1] = 1
...     i = np.arange(n - 1)
...     sparsity[i, i + 1] = 1
...     return sparsity
...
>>> n = 100000
>>> x0_broyden = -np.ones(n)
...
>>> res_3 = least_squares(fun_broyden, x0_broyden,
...                       jac_sparsity=sparsity_broyden(n))
>>> res_3.cost
4.5687069299604613e-23
>>> res_3.optimality
1.1650454296851518e-11

Давайте также решим задачу аппроксимации кривой с использованием устойчивой функции потерь, чтобы учесть выбросы в данных. Определим модельную функцию как y = a + b * exp(c * t), где t - переменная-предиктор, y - наблюдение, а a, b, c - параметры для оценки.

Сначала определите функцию, которая генерирует данные с шумом и выбросами, определите параметры модели и сгенерируйте данные:

>>> from numpy.random import default_rng
>>> rng = default_rng()
>>> def gen_data(t, a, b, c, noise=0., n_outliers=0, seed=None):
...     rng = default_rng(seed)
...
...     y = a + b * np.exp(t * c)
...
...     error = noise * rng.standard_normal(t.size)
...     outliers = rng.integers(0, t.size, n_outliers)
...     error[outliers] *= 10
...
...     return y + error
...
>>> a = 0.5
>>> b = 2.0
>>> c = -1
>>> t_min = 0
>>> t_max = 10
>>> n_points = 15
...
>>> t_train = np.linspace(t_min, t_max, n_points)
>>> y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3)

Определить функцию для вычисления остатков и начальной оценки параметров.

>>> def fun(x, t, y):
...     return x[0] + x[1] * np.exp(x[2] * t) - y
...
>>> x0 = np.array([1.0, 1.0, 0.0])

Вычислить стандартное решение методом наименьших квадратов:

>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train))

Теперь вычислим два решения с двумя различными функциями потерь робастности. Параметр f_scale установлено в 0.1, что означает, что остатки выбросов не должны значительно превышать 0.1 (уровень шума, используемый).

>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1,
...                             args=(t_train, y_train))
>>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1,
...                         args=(t_train, y_train))

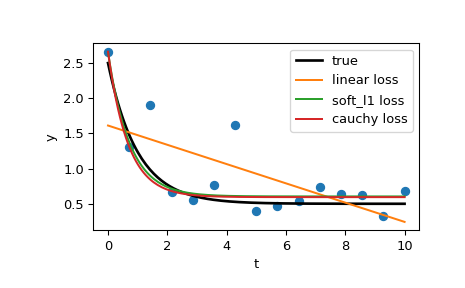
И, наконец, построим все кривые. Мы видим, что, выбирая подходящий потеря мы можем получить оценки, близкие к оптимальным, даже при наличии сильных выбросов. Но имейте в виду, что обычно рекомендуется сначала попробовать функции потерь 'soft_l1' или 'huber' (если это вообще необходимо), так как другие два варианта могут вызвать трудности в процессе оптимизации.

>>> t_test = np.linspace(t_min, t_max, n_points * 10)
>>> y_true = gen_data(t_test, a, b, c)
>>> y_lsq = gen_data(t_test, *res_lsq.x)
>>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x)
>>> y_log = gen_data(t_test, *res_log.x)
...
>>> import matplotlib.pyplot as plt
>>> plt.plot(t_train, y_train, 'o')
>>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true')
>>> plt.plot(t_test, y_lsq, label='linear loss')
>>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss')
>>> plt.plot(t_test, y_log, label='cauchy loss')
>>> plt.xlabel("t")
>>> plt.ylabel("y")
>>> plt.legend()
>>> plt.show()

В следующем примере мы покажем, как комплекснозначные функции невязки комплексных переменных могут быть оптимизированы с помощью least_squares(). Рассмотрим следующую функцию:

>>> def f(z):
...     return z - (0.5 + 0.5j)

Мы оборачиваем его в функцию вещественных переменных, которая возвращает вещественные невязки, просто обрабатывая вещественную и мнимую части как независимые переменные:

>>> def f_wrap(x):
...     fx = f(x[0] + 1j*x[1])
...     return np.array([fx.real, fx.imag])

Таким образом, вместо исходной m-D комплексной функции n комплексных переменных мы оптимизируем 2m-D вещественную функцию 2n вещественных переменных:

>>> from scipy.optimize import least_squares
>>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1]))
>>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j
>>> z
(0.49999999999925893+0.49999999999925893j)

НазадОткрыть во вкладке