scipy.signal.ShortTimeFFT.

from_dual

метод класса ShortTimeFFT.from_dual(dual_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)

Создать экземпляр ShortTimeFFT только предоставив двойное окно.

Если STFT обратим, можно вычислить окно win из заданного двойного окна dual_win. Все остальные параметры имеют то же значение, что и в инициализаторе ShortTimeFFT.

Как объясняется в Кратковременное преобразование Фурье раздел Руководство пользователя SciPy, инвертируемое STFT можно интерпретировать как разложение в ряд сдвинутых во времени и модулированных по частоте двойных окон. Например, коэффициент ряда S[q,p] принадлежит члену, который сдвинут dual_win by p * delta_t и умножил его на exp( 2 * j * pi * t * q * delta_f).

Смотрите также

from_window

Создать экземпляр путём обёртывания get_window.

ShortTimeFFT

Создать экземпляр с помощью стандартного инициализатора.

Примеры

Попробуйте в вашем браузере!

Следующий пример рассматривает разложение сигнала на сдвинутые по времени и частоте гауссианы. Гауссиан со стандартным отклонением единица, состоящий из 51 выборки, будет использоваться:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T, N = 0.1, 51
>>> d_win = gaussian(N, std=1/T, sym=True)  # symmetric Gaussian window
>>> t = T * (np.arange(N) - N//2)
...
>>> fg1, ax1 = plt.subplots()
>>> ax1.set_title(r"Dual Window: Gaussian with $\sigma_t=1$")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...        xlim=(t[0], t[-1]), ylim=(0, 1.1*np.max(d_win)))
>>> ax1.plot(t, d_win, 'C0-')

Следующий график с перекрытием 41, 11 и 2 выборок показывает, как hop интервал влияет на форму окна win:

>>> fig2, axx = plt.subplots(3, 1, sharex='all')
...
>>> axx[0].set_title(r"Windows for hop$\in\{10, 40, 49\}$")
>>> for c_, h_ in enumerate([10, 40, 49]):
...     SFT = ShortTimeFFT.from_dual(d_win, h_, 1/T)
...     axx[c_].plot(t + h_ * T, SFT.win, 'k--', alpha=.3, label=None)
...     axx[c_].plot(t - h_ * T, SFT.win, 'k:', alpha=.3, label=None)
...     axx[c_].plot(t, SFT.win, f'C{c_+1}',
...                     label=r"$\Delta t=%0.1f\,$s" % SFT.delta_t)
...     axx[c_].set_ylim(0, 1.1*max(SFT.win))
...     axx[c_].legend(loc='center')
>>> axx[-1].set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...             xlim=(t[0], t[-1]))
>>> plt.show()

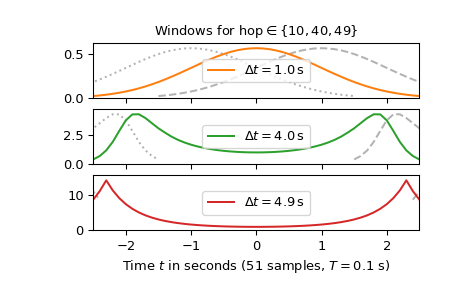
Помимо окна win центрирован в t = 0, предыдущий (t = -delta_t) и следующее окно (t = delta_t) изображены. Видно, что для малых hop интервалах, окно является компактным и гладким, обладая хорошей концентрацией во времени и частоте в STFT. Для больших hop интервал 4.9 с, окно имеет малые значения около t = 0, которые не покрываются перекрытием соседних окон, что может привести к численным неточностям. Кроме того, пикообразная форма в начале и конце окна указывает на более высокую полосу пропускания, что приводит к худшему разрешению по времени-частоте STFT. Следовательно, выбор hop Интервал будет компромиссом между разрешением по времени-частоте и требованиями к памяти, предъявляемыми малыми hop размеры.

НазадОткрыть во вкладке