scipy.signal.

ShortTimeFFT#

класс scipy.signal.ShortTimeFFT(win, hop, fs, *, fft_mode='onesided', mfft=None, dual_win=None, scale_to=None, phase_shift=0)[источник]#

Предоставить параметризованное дискретное коротковременное преобразование Фурье (stft) и его обратное преобразование (istft).

The stft вычисляет последовательные БПФ, скользя окном (win) над входным сигналом путем hop приращения. Может использоваться для количественной оценки изменения спектра во времени.

The stft представлена комплекснозначной матрицей S[q,p], где p-й столбец представляет FFT с окном, центрированным в момент времени t[p] = p * delta_t = p * hop * T где T это интервал дискретизации входного сигнала. Строка q представляет значения на частоте f[q] = q * delta_f с delta_f = 1 / (mfft * T) является шириной бина БПФ.

Обратное коротковременное преобразование Фурье istft рассчитывается путем обращения шагов STFT: взять обратное БПФ p-го среза S[q,p] и умножить результат на так называемое двойное окно (см. dual_win). Сдвинуть результат на p * delta_t и добавить результат к предыдущим сдвинутым результатам для восстановления сигнала. Если известна только двойная оконная функция и STFT является обратимым, from_dual может использоваться для создания экземпляра этого класса.

По умолчанию используется так называемое каноническое двойное окно. Это окно с минимальной энергией среди всех возможных двойных окон. from_win_equals_dual и closest_STFT_dual_window предоставляет средства для использования альтернативных двойных окон. Обратите внимание, что win также всегда является двойным окном для dual_win.

Из-за соглашения, что время t = 0 соответствует первому отсчёту входного сигнала, значения STFT обычно имеют отрицательные временные слоты. Следовательно, отрицательные индексы, такие как p_min или k_min не указывают на подсчёт в обратном порядке от конца массива, как в стандартной индексации Python, а на нахождение слева от t = 0.

Более подробную информацию можно найти в Кратковременное преобразование Фурье раздел Руководство пользователя SciPy.

Обратите внимание, что все параметры инициализатора, кроме scale_to (который использует scaling) имеют идентичные именованные атрибуты.

Параметры:

winnp.ndarray: Окно должно быть вещественным или комплексным одномерным массивом.
hopint: Приращение в выборках, на которое окно сдвигается на каждом шаге.
fsfloat: Частота дискретизации входного сигнала и окна. Её связь с интервалом дискретизации T является T = 1 / fs.
fft_mode'twosided', 'centered', 'onesided', 'onesided2X': Режим БПФ для использования (по умолчанию 'onesided'). См. свойство fft_mode подробности.
mfft: int | None: Длина БПФ, используемого, если требуется дополненный нулями БПФ. Если None (по умолчанию), длина окна win используется.
dual_winnp.ndarray | None: Двойное окно win. Если установлено в None, он вычисляется при необходимости.
scale_to‘magnitude’, ‘psd’ | None: Если не None (по умолчанию) оконная функция масштабируется, так что каждый столбец STFT представляет либо спектр 'magnitude', либо спектральную плотность мощности ('psd'). Этот параметр устанавливает свойство scaling до того же значения. См. метод scale_to подробности.
phase_shiftint | None: Если установлено, добавить линейную фазу phase_shift / mfft * f для каждой частоты f. Значение по умолчанию 0 гарантирует отсутствие фазового сдвига на нулевом срезе (где t=0 центрировано). См. свойство phase_shift для получения дополнительной информации.

Атрибуты:

T: Интервал дискретизации входного сигнала и окна.
delta_f: Ширина частотных бинов STFT.
delta_t: Временной прирост STFT.
dual_win: Двойное окно (по умолчанию каноническое двойное окно).
f: Значения частот STFT.
f_pts: Количество точек вдоль оси частот.
fac_magnitude: Коэффициент для умножения значений STFT для масштабирования каждого частотного среза до спектра амплитуд.
fac_psd: Множитель для умножения значений STFT для масштабирования каждого частотного среза до спектральной плотности мощности (PSD).
fft_mode: Режим используемого БПФ ('twosided', 'centered', 'onesided' или 'onesided2X').
fs: Частота дискретизации входного сигнала и окна.
hop: Временной прирост в выборках сигнала для скользящего окна.
invertible: Проверить, является ли STFT обратимым.
k_min: Наименьший возможный индекс сигнала STFT.
lower_border_end: Первый индекс сигнала и первый индекс среза не затрагиваются предварительным заполнением.
m_num: Количество выборок в окне win.
m_num_mid: Центральный индекс окна win.
mfft: Длина входных данных для БПФ, используемого - может быть больше длины окна m_num.
onesided_fft: Возвращает True, если используется одностороннее БПФ.
p_min: Наименьший возможный индекс среза.
phase_shift: Если установлено, добавить линейную фазу phase_shift / mfft * f для каждого среза БПФ частоты f.
scaling: Нормализация, применяемая к оконной функции ('magnitude', 'psd', 'unitary', или None).
win: Оконная функция как вещественный или комплексный одномерный массив.

Методы

`extent`(n[, axes_seq, center_bins])	Возвращает минимальные и максимальные значения времени-частоты.
`from_dual`(dual_win, hop, fs, *[, fft_mode, ...])	Создать экземпляр ShortTimeFFT только предоставив двойное окно.
`from_win_equals_dual`(desired_win, hop, fs, *)	Создать экземпляр, где окно и его дуальное окно равны с точностью до масштабного коэффициента.
`from_window`(win_param, fs, nperseg, noverlap, *)	Создайте экземпляр ShortTimeFFT используя get_window.
`istft`(S[, k0, k1, f_axis, t_axis])	Обратное коротковременное преобразование Фурье.
`k_max`(n)	Первый индекс выборки после конца сигнала, не затронутый временным срезом.
`nearest_k_p`(k[, left])	Возвращает ближайший индекс выборки k_p, для которого выполняется t[k_p] == t[p].
`p_max`(n)	Индекс первого неперекрывающегося верхнего временного среза для n пример входных данных.
`p_num`(n)	Количество временных срезов для входного сигнала с n выборки.
`p_range`(n[, p0, p1])	Определить и проверить диапазон индексов среза.
`scale_to`(масштабирование)	Масштабировать окно для получения 'magnitude' или 'psd' масштабирования для STFT.
`spectrogram`(x[, y, detr, p0, p1, k_offset, ...])	Вычислить спектрограмму или кросс-спектрограмму.
`stft`(x[, p0, p1, k_offset, padding, axis])	Выполнить кратковременное преобразование Фурье.
`stft_detrend`(x, detr[, p0, p1, k_offset, ...])	Вычислить кратковременное преобразование Фурье с предварительным вычитанием тренда из каждого сегмента.
`t`(n[, p0, p1, k_offset])	Времена STFT для входного сигнала с n выборки.
`upper_border_begin`(n)	Первый индекс сигнала и первый индекс среза, затронутые пост-дополнением.

Примечания

Типичное применение STFT — создание различных типов графиков время-частота, часто объединяемых под термином «спектрограмма». Обратите внимание, что этот термин также используется для явного обозначения абсолютного квадрата STFT [11], как сделано в spectrogram.

STFT также может использоваться для фильтрации и банков фильтров, как обсуждается в [12].

Ссылки

[11]

Карлхайнц Грёхениг: "Основы анализа время-частота", Birkhäuser Boston 2001, 10.1007/978-1-4612-0003-1

[12]

Julius O. Smith III, “Spectral Audio Signal Processing”, онлайн-книга, 2011, https://www.dsprelated.com/freebooks/sasp/

Примеры

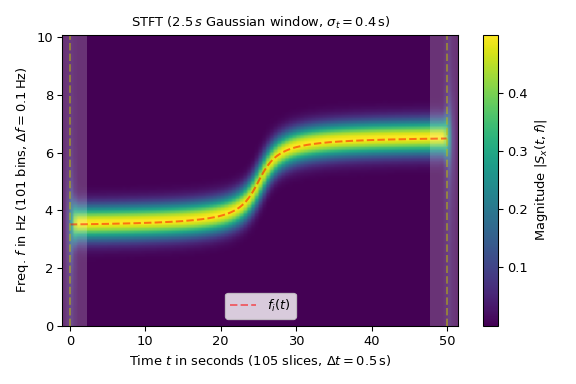
Следующий пример показывает величину STFT синусоиды с изменяющейся частотой \(f_i(t)\) (отмечено красной пунктирной линией на графике):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 1 * np.arctan((t_x - t_x[N // 2]) / 2) + 5  # varying frequency
>>> x = np.sin(2*np.pi*np.cumsum(f_i)*T_x) # the signal

Используемое окно Гаусса имеет длину 50 выборок или 2.5 с. Параметр mfft=200 в ShortTimeFFT приводит к передискретизации спектра в 4 раза:

>>> g_std = 8  # standard deviation for Gaussian window in samples
>>> w = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian window
>>> SFT = ShortTimeFFT(w, hop=10, fs=1/T_x, mfft=200, scale_to='magnitude')
>>> Sx = SFT.stft(x)  # perform the STFT

На графике временной охват сигнала x отмечен вертикальными пунктирными линиями. Обратите внимание, что SFT даёт значения за пределами временного диапазона x. Затененные области слева и справа указывают на граничные эффекты, вызванные тем, что срезы окна в этой области не полностью находятся внутри временного диапазона x:

>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"STFT ({SFT.m_num*SFT.T:g}$\,s$ Gaussian window, " +
...               rf"$\sigma_t={g_std*SFT.T}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
...
>>> im1 = ax1.imshow(abs(Sx), origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='viridis')
>>> ax1.plot(t_x, f_i, 'r--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label="Magnitude $|S_x(t, f)|$")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.2)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line:
...     ax1.axvline(t_, color='y', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

../../_images/scipy-signal-ShortTimeFFT-1_00_00.png

Восстановление сигнала с помощью istft просто, но обратите внимание, что длина x1 должен быть указан, поскольку длина STFT увеличивается в hop шаги:

>>> SFT.invertible  # check if invertible
True
>>> x1 = SFT.istft(Sx, k1=N)
>>> np.allclose(x, x1)
True

Возможно вычислить STFT частей сигнала:

>>> N2 = SFT.nearest_k_p(N // 2)
>>> Sx0 = SFT.stft(x[:N2])
>>> Sx1 = SFT.stft(x[N2:])

При объединении последовательных частей STFT необходимо учитывать перекрытие:

>>> p0_ub = SFT.upper_border_begin(N2)[1] - SFT.p_min
>>> p1_le = SFT.lower_border_end[1] - SFT.p_min
>>> Sx01 = np.hstack((Sx0[:, :p0_ub],
...                   Sx0[:, p0_ub:] + Sx1[:, :p1_le],
...                   Sx1[:, p1_le:]))
>>> np.allclose(Sx01, Sx)  # Compare with SFT of complete signal
True

Также возможно вычислить itsft для частей сигнала:

>>> y_p = SFT.istft(Sx, N//3, N//2)
>>> np.allclose(y_p, x[N//3:N//2])
True