Обработка сигналов (scipy.signal)

Текущий набор инструментов обработки сигналов содержит некоторые функции фильтрации, ограниченный набор инструментов проектирования фильтров и несколько алгоритмов интерполяции B-сплайнами для 1- и 2-мерных данных. Хотя алгоритмы B-сплайнов технически можно отнести к категории интерполяции, они включены сюда, потому что они работают только с равноотстоящими данными и активно используют теорию фильтров и формализм передаточной функции для обеспечения быстрого преобразования B-сплайна. Чтобы понять этот раздел, вам нужно понимать, что сигнал в SciPy — это массив действительных или комплексных чисел.

B-сплайны

B-сплайн — это аппроксимация непрерывной функции на конечной области через B-сплайн коэффициенты и узловые точки. Если узловые точки расположены равномерно с шагом \(\Delta x\), тогда B-сплайн аппроксимация 1-D функции является конечнобазисным разложением.

\[y\left(x\right)\approx\sum_{j}c_{j}\beta^{o}\left(\frac{x}{\Delta x}-j\right).\]

В двух измерениях с интервалом между узлами \(\Delta x\) и \(\Delta y\), представление функции

\[z\left(x,y\right)\approx\sum_{j}\sum_{k}c_{jk}\beta^{o}\left(\frac{x}{\Delta x}-j\right)\beta^{o}\left(\frac{y}{\Delta y}-k\right).\]

В этих выражениях \(\beta^{o}\left(\cdot\right)\) является ограниченной по пространству B-сплайн базисной функцией порядка \(o\). Требование равномерно распределенных узлов сплайна и равномерно распределенных точек данных позволяет разработать быстрые алгоритмы (обратной фильтрации) для определения коэффициентов, \(c_{j}\), из выборочных значений, \(y_{n}\). В отличие от общих алгоритмов сплайн-интерполяции, эти алгоритмы могут быстро находить коэффициенты сплайна для больших изображений.

Преимущество представления набора выборок через B-сплайн базисные функции заключается в том, что операторы непрерывной области (производные, пере- дискретизация, интеграл и т.д.), которые предполагают, что выборки данных взяты из непрерывной функции, могут быть вычислены относительно легко из коэффициентов сплайна. Например, вторая производная сплайна — это

\[y{}^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\beta^{o\prime\prime}\left(\frac{x}{\Delta x}-j\right).\]

Используя свойство B-сплайнов, что

\[\frac{d^{2}\beta^{o}\left(w\right)}{dw^{2}}=\beta^{o-2}\left(w+1\right)-2\beta^{o-2}\left(w\right)+\beta^{o-2}\left(w-1\right),\]

можно увидеть, что

\[y^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\left[\beta^{o-2}\left(\frac{x}{\Delta x}-j+1\right)-2\beta^{o-2}\left(\frac{x}{\Delta x}-j\right)+\beta^{o-2}\left(\frac{x}{\Delta x}-j-1\right)\right].\]

Если \(o=3\), тогда в точках выборки:

\begin{eqnarray*} \Delta x^{2}\left.y^{\prime}\left(x\right)\right|_{x=n\Delta x} & = & \sum_{j}c_{j}\delta_{n-j+1}-2c_{j}\delta_{n-j}+c_{j}\delta_{n-j-1},\\ & = & c_{n+1}-2c_{n}+c_{n-1}.\end{eqnarray*}

Таким образом, сигнал второй производной может быть легко вычислен из сплайн-аппроксимации. При необходимости можно найти сглаживающие сплайны, чтобы сделать вторую производную менее чувствительной к случайным ошибкам.

Внимательный читатель уже заметил, что выборки данных связаны с коэффициентами узлов через оператор свертки, так что простая свертка с дискретизированной B-сплайн функцией восстанавливает исходные данные из коэффициентов сплайна. Результат свертки может меняться в зависимости от того, как обрабатываются границы (это становится все более важным с увеличением количества измерений в наборе данных). Алгоритмы, связанные с B-сплайнами в подпакете обработки сигналов, предполагают зеркально-симметричные граничные условия. Таким образом, коэффициенты сплайна вычисляются на основе этого предположения, и выборки данных могут быть точно восстановлены из коэффициентов сплайна, предполагая их также зеркально-симметричными.

В настоящее время пакет предоставляет функции для определения коэффициентов кубических сплайнов второго и третьего порядка из равноотстоящих выборок в одном и двух измерениях (qspline1d, qspline2d, cspline1d, cspline2d). Для больших \(o\), базисная функция B-сплайна может быть хорошо аппроксимирована гауссовой функцией с нулевым средним и стандартным отклонением, равным \(\sigma_{o}=\left(o+1\right)/12\) :

\[\beta^{o}\left(x\right)\approx\frac{1}{\sqrt{2\pi\sigma_{o}^{2}}}\exp\left(-\frac{x^{2}}{2\sigma_{o}}\right).\]

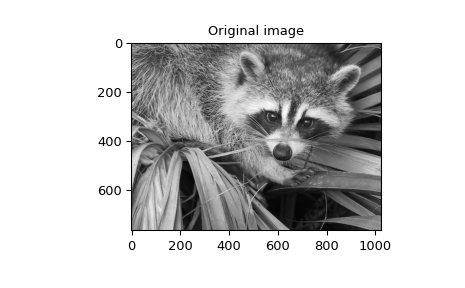
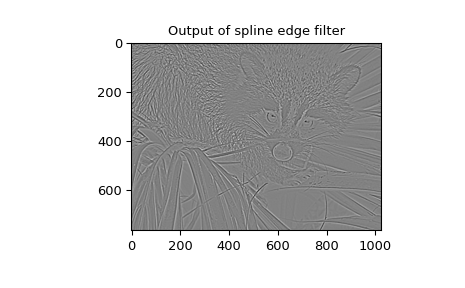
Функция для вычисления этого гауссова распределения для произвольного \(x\) и \(o\) также доступен ( gauss_spline ). Следующий код и рисунок используют сплайн-фильтрацию для вычисления краевого изображения (вторая производная сглаженного сплайна) морды енота, которое является массивом, возвращаемым командой scipy.datasets.face. Команда sepfir2d использовался для применения сепарабельного 2-D КИХ-фильтра с зеркально-симметричными граничными условиями к коэффициентам сплайна. Эта функция идеально подходит для восстановления выборок из коэффициентов сплайна и быстрее, чем convolve2d, который свертывает произвольные 2-D фильтры и позволяет выбирать зеркально-симметричные граничные условия.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True).astype(np.float32)
>>> derfilt = np.array([1.0, -2, 1.0], dtype=np.float32)
>>> ck = signal.cspline2d(image, 8.0)
>>> deriv = (signal.sepfir2d(ck, derfilt, [1]) +
...          signal.sepfir2d(ck, [1], derfilt))

В качестве альтернативы мы могли бы сделать:

laplacian = np.array([[0,1,0], [1,-4,1], [0,1,0]], dtype=np.float32)
deriv2 = signal.convolve2d(ck,laplacian,mode='same',boundary='symm')

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(deriv)
>>> plt.gray()
>>> plt.title('Output of spline edge filter')
>>> plt.show()

Фильтрация

Фильтрация — это общее название для любой системы, которая каким-либо образом изменяет входной сигнал. В SciPy сигнал можно рассматривать как массив NumPy. Существуют различные виды фильтров для различных операций. Существует два основных вида операций фильтрации: линейные и нелинейные. Линейные фильтры всегда могут быть сведены к умножению развёрнутого массива NumPy на соответствующую матрицу, что даёт другой развёрнутый массив NumPy. Конечно, это обычно не лучший способ вычисления фильтра, так как задействованные матрицы и векторы могут быть огромными. Например, фильтрация \(512 \times 512\) изображение с этим методом потребовало бы умножения \(512^2 \times 512^2\) матрица с \(512^2\) вектор. Просто попытка сохранить \(512^2 \times 512^2\) матрица с использованием стандартного массива NumPy потребовала бы \(68,719,476,736\) элементов. При 4 байтах на элемент это потребует \(256\textrm{GB}\) памяти. В большинстве приложений большинство элементов этой матрицы равны нулю, и используется другой метод для вычисления выхода фильтра.

Свёртка/Корреляция

Многие линейные фильтры также обладают свойством инвариантности к сдвигу. Это означает, что операция фильтрации одинакова в разных местах сигнала и подразумевает, что матрица фильтрации может быть построена на основе знания одной строки (или столбца) матрицы. В этом случае умножение матриц может быть выполнено с использованием преобразований Фурье.

Пусть \(x\left[n\right]\) определить 1-D сигнал, индексируемый целым числом \(n.\) Полная свёртка двух 1-D сигналов может быть выражена как

\[y\left[n\right]=\sum_{k=-\infty}^{\infty}x\left[k\right]h\left[n-k\right].\]

Это уравнение может быть реализовано напрямую только если мы ограничим последовательности конечными последовательностями, которые могут быть сохранены в компьютере, выберем \(n=0\) быть начальной точкой обеих последовательностей, пусть \(K+1\) будет тем значением, для которого \(x\left[n\right]=0\) для всех \(n\geq K+1\) и \(M+1\) будет тем значением, для которого \(h\left[n\right]=0\) для всех \(n\geq M+1\), тогда выражение дискретной свертки имеет вид

\[y\left[n\right]=\sum_{k=\max\left(n-M,0\right)}^{\min\left(n,K\right)}x\left[k\right]h\left[n-k\right].\]

Для удобства, предположим \(K\geq M.\) Тогда, более явно, результат этой операции

\begin{eqnarray*} y\left[0\right] & = & x\left[0\right]h\left[0\right]\\ y\left[1\right] & = & x\left[0\right]h\left[1\right]+x\left[1\right]h\left[0\right]\\ y\left[2\right] & = & x\left[0\right]h\left[2\right]+x\left[1\right]h\left[1\right]+x\left[2\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[M\right] & = & x\left[0\right]h\left[M\right]+x\left[1\right]h\left[M-1\right]+\cdots+x\left[M\right]h\left[0\right]\\ y\left[M+1\right] & = & x\left[1\right]h\left[M\right]+x\left[2\right]h\left[M-1\right]+\cdots+x\left[M+1\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[K\right] & = & x\left[K-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[0\right]\\ y\left[K+1\right] & = & x\left[K+1-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[1\right]\\ \vdots & \vdots & \vdots\\ y\left[K+M-1\right] & = & x\left[K-1\right]h\left[M\right]+x\left[K\right]h\left[M-1\right]\\ y\left[K+M\right] & = & x\left[K\right]h\left[M\right].\end{eqnarray*}

Таким образом, полная дискретная свертка двух конечных последовательностей длин \(K+1\) и \(M+1\), соответственно, приводит к конечной последовательности длины \(K+M+1=\left(K+1\right)+\left(M+1\right)-1.\)

1-D свёртка реализована в SciPy с функцией convolve. Эта функция принимает в качестве входных данных сигналы \(x,\) \(h\), и два необязательных флага 'mode' и 'method', и возвращает сигнал \(y.\)

Первый необязательный флаг, 'mode', позволяет указать, какую часть выходного сигнала возвращать. Значение по умолчанию 'full' возвращает весь сигнал. Если флаг имеет значение 'same', то только средняя \(K\) значения возвращаются, начиная с \(y\left[\left\lfloor \frac{M-1}{2}\right\rfloor \right]\), чтобы выход имел ту же длину, что и первый вход. Если флаг имеет значение 'valid', то только средняя \(K-M+1=\left(K+1\right)-\left(M+1\right)+1\) возвращаются выходные значения, где \(z\) зависит от всех значений наименьшего ввода из \(h\left[0\right]\) to \(h\left[M\right].\) Другими словами, только значения \(y\left[M\right]\) to \(y\left[K\right]\) включительно возвращаются.

Второй необязательный флаг, 'method', определяет, как вычисляется свертка: либо через подход преобразования Фурье с fftconvolve или через прямой метод. По умолчанию выбирает ожидаемо более быстрый метод. Метод преобразования Фурье имеет порядок \(O(N\log N)\), в то время как прямой метод имеет порядок \(O(N^2)\). В зависимости от константы большого O и значения \(N\), один из этих двух методов может быть быстрее. Значение по умолчанию ‘auto’ выполняет грубый расчет и выбирает ожидаемо более быстрый метод, в то время как значения ‘direct’ и ‘fft’ принудительно используют два других метода.

Код ниже показывает простой пример свёртки 2 последовательностей:

>>> x = np.array([1.0, 2.0, 3.0])
>>> h = np.array([0.0, 1.0, 0.0, 0.0, 0.0])
>>> signal.convolve(x, h)
array([ 0.,  1.,  2.,  3.,  0.,  0.,  0.])
>>> signal.convolve(x, h, 'same')
array([ 2.,  3.,  0.])

Эта же функция convolve может принимать N-мерные массивы в качестве входных данных и возвращать N-мерную свертку двух массивов, как показано в примере кода ниже. Для этого случая доступны те же флаги входных данных.

>>> x = np.array([[1., 1., 0., 0.], [1., 1., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]])
>>> h = np.array([[1., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 0.]])
>>> signal.convolve(x, h)
array([[ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]])

Корреляция очень похожа на свертку, за исключением того, что знак минус становится знаком плюс. Таким образом,

\[w\left[n\right]=\sum_{k=-\infty}^{\infty}y\left[k\right]x\left[n+k\right],\]

является (кросс)корреляцией сигналов \(y\) и \(x.\) Для сигналов конечной длины с \(y\left[n\right]=0\) вне диапазона \(\left[0,K\right]\) и \(x\left[n\right]=0\) вне диапазона \(\left[0,M\right],\) суммирование может упроститься до

\[w\left[n\right]=\sum_{k=\max\left(0,-n\right)}^{\min\left(K,M-n\right)}y\left[k\right]x\left[n+k\right].\]

Предполагая снова, что \(K\geq M\), это

\begin{eqnarray*} w\left[-K\right] & = & y\left[K\right]x\left[0\right]\\ w\left[-K+1\right] & = & y\left[K-1\right]x\left[0\right]+y\left[K\right]x\left[1\right]\\ \vdots & \vdots & \vdots\\ w\left[M-K\right] & = & y\left[K-M\right]x\left[0\right]+y\left[K-M+1\right]x\left[1\right]+\cdots+y\left[K\right]x\left[M\right]\\ w\left[M-K+1\right] & = & y\left[K-M-1\right]x\left[0\right]+\cdots+y\left[K-1\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[-1\right] & = & y\left[1\right]x\left[0\right]+y\left[2\right]x\left[1\right]+\cdots+y\left[M+1\right]x\left[M\right]\\ w\left[0\right] & = & y\left[0\right]x\left[0\right]+y\left[1\right]x\left[1\right]+\cdots+y\left[M\right]x\left[M\right]\\ w\left[1\right] & = & y\left[0\right]x\left[1\right]+y\left[1\right]x\left[2\right]+\cdots+y\left[M-1\right]x\left[M\right]\\ w\left[2\right] & = & y\left[0\right]x\left[2\right]+y\left[1\right]x\left[3\right]+\cdots+y\left[M-2\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[M-1\right] & = & y\left[0\right]x\left[M-1\right]+y\left[1\right]x\left[M\right]\\ w\left[M\right] & = & y\left[0\right]x\left[M\right].\end{eqnarray*}

Функция SciPy correlate реализует эту операцию. Эквивалентные флаги доступны для этой операции, чтобы вернуть полный \(K+M+1\) длина последовательности ('full') или последовательность того же размера, что и наибольшая последовательность, начинающаяся с \(w\left[-K+\left\lfloor \frac{M-1}{2}\right\rfloor \right]\) (‘same’) или последовательность, где значения зависят от всех значений наименьшей последовательности (‘valid’). Этот последний вариант возвращает \(K-M+1\) values \(w\left[M-K\right]\) to \(w\left[0\right]\) включительно.

Функция correlate также может принимать произвольные N-мерные массивы в качестве входных данных и возвращать N-мерную свёртку двух массивов на выходе.

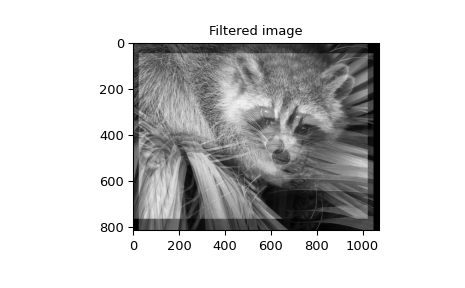
Когда \(N=2,\) correlate и/или convolve может использоваться для создания произвольных фильтров изображений для выполнения таких действий, как размытие, улучшение и обнаружение краёв изображения.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True)
>>> w = np.zeros((50, 50))
>>> w[0][0] = 1.0
>>> w[49][25] = 1.0
>>> image_new = signal.fftconvolve(image, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

Вычисление свертки во временной области, как указано выше, в основном используется для фильтрации, когда один из сигналов значительно меньше другого ( \(K\gg M\) ), в противном случае линейная фильтрация более эффективно вычисляется в частотной области, предоставляемой функцией fftconvolve. По умолчанию, convolve оценивает самый быстрый метод, используя choose_conv_method.

Если функция фильтра \(w[n,m]\) может быть факторизован согласно

\[h[n, m] = h_1[n] h_2[m],\]

свертку можно вычислить с помощью функции sepfir2d. В качестве примера рассмотрим гауссовский фильтр gaussian

\[h[n, m] \propto e^{-x^2-y^2} = e^{-x^2} e^{-y^2},\]

которое часто используется для размытия.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = np.asarray(datasets.ascent(), np.float64)
>>> w = signal.windows.gaussian(51, 10.0)
>>> image_new = signal.sepfir2d(image, w, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

Фильтрация по разностному уравнению

Общий класс линейных одномерных фильтров (включающий свёрточные фильтры) — это фильтры, описываемые разностным уравнением

\[\sum_{k=0}^{N}a_{k}y\left[n-k\right]=\sum_{k=0}^{M}b_{k}x\left[n-k\right],\]

где \(x\left[n\right]\) является входной последовательностью, а \(y\left[n\right]\) является выходной последовательностью. Если предположить начальный покой, так что \(y\left[n\right]=0\) для \(n<0\), тогда такой фильтр можно реализовать с помощью свертки. Однако последовательность фильтра свертки \(h\left[n\right]\) может быть бесконечным, если \(a_{k}\neq0\) для \(k\geq1.\) Кроме того, этот общий класс линейных фильтров позволяет устанавливать начальные условия на \(y\left[n\right]\) для \(n<0\) что приводит к фильтру, который нельзя выразить с помощью свертки.

Разностное уравнение фильтра можно рассматривать как нахождение \(y\left[n\right]\) рекурсивно через его предыдущие значения

\[a_{0}y\left[n\right]=-a_{1}y\left[n-1\right]-\cdots-a_{N}y\left[n-N\right]+\cdots+b_{0}x\left[n\right]+\cdots+b_{M}x\left[n-M\right].\]

Часто, \(a_{0}=1\) выбирается для нормализации. Реализация в SciPy этого общего фильтра разностного уравнения немного сложнее, чем можно было бы предположить из предыдущего уравнения. Она реализована так, что только один сигнал нуждается в задержке. Фактические уравнения реализации (предполагая \(a_{0}=1\) ):

\begin{eqnarray*} y\left[n\right] & = & b_{0}x\left[n\right]+z_{0}\left[n-1\right]\\ z_{0}\left[n\right] & = & b_{1}x\left[n\right]+z_{1}\left[n-1\right]-a_{1}y\left[n\right]\\ z_{1}\left[n\right] & = & b_{2}x\left[n\right]+z_{2}\left[n-1\right]-a_{2}y\left[n\right]\\ \vdots & \vdots & \vdots\\ z_{K-2}\left[n\right] & = & b_{K-1}x\left[n\right]+z_{K-1}\left[n-1\right]-a_{K-1}y\left[n\right]\\ z_{K-1}\left[n\right] & = & b_{K}x\left[n\right]-a_{K}y\left[n\right],\end{eqnarray*}

где \(K=\max\left(N,M\right).\) Обратите внимание, что \(b_{K}=0\) if \(K>M\) и \(a_{K}=0\) if \(K>N.\) Таким образом, выход в момент времени \(n\) зависит только от входных данных в момент времени \(n\) и значение \(z_{0}\) в предыдущий момент времени. Это всегда можно рассчитать, пока \(K\) values \(z_{0}\left[n-1\right]\ldots z_{K-1}\left[n-1\right]\) вычисляются и сохраняются на каждом временном шаге.

Фильтр разностного уравнения вызывается командой lfilter в SciPy. Эта команда принимает в качестве входных данных вектор \(b,\) вектор, \(a,\) сигнал \(x\) и возвращает вектор \(y\) (такой же длины, как \(x\) ) вычисляется с использованием приведённого выше уравнения. Если \(x\) если N-D, то фильтр вычисляется вдоль указанной оси. При необходимости начальные условия, предоставляющие значения \(z_{0}\left[-1\right]\) to \(z_{K-1}\left[-1\right]\) могут быть предоставлены или же будет предполагаться, что они все равны нулю. Если начальные условия предоставлены, то конечные условия на промежуточные переменные также возвращаются. Они могут быть использованы, например, для перезапуска вычисления в том же состоянии.

Иногда удобнее выразить начальные условия через сигналы \(x\left[n\right]\) и \(y\left[n\right].\) Другими словами, возможно, у вас есть значения \(x\left[-M\right]\) to \(x\left[-1\right]\) и значения \(y\left[-N\right]\) to \(y\left[-1\right]\) и хотел бы определить, какие значения \(z_{m}\left[-1\right]\) должны быть предоставлены как начальные условия для разностно-уравненного фильтра. Несложно показать, что для \(0\leq m

\[z_{m}\left[n\right]=\sum_{p=0}^{K-m-1}\left(b_{m+p+1}x\left[n-p\right]-a_{m+p+1}y\left[n-p\right]\right).\]

Используя эту формулу, мы можем найти вектор начальных условий \(z_{0}\left[-1\right]\) to \(z_{K-1}\left[-1\right]\) при заданных начальных условиях на \(y\) (и \(x\) ). Команда lfiltic выполняет эту функцию.

В качестве примера рассмотрим следующую систему:

\[y[n] = \frac{1}{2} x[n] + \frac{1}{4} x[n-1] + \frac{1}{3} y[n-1]\]

Код вычисляет сигнал \(y[n]\) для заданного сигнала \(x[n]\); сначала для начальных условий \(y[-1] = 0\) (случай по умолчанию), тогда для \(y[-1] = 2\) посредством lfiltic.

>>> import numpy as np
>>> from scipy import signal

>>> x = np.array([1., 0., 0., 0.])
>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.lfilter(b, a, x)
array([0.5, 0.41666667, 0.13888889, 0.0462963])
>>> zi = signal.lfiltic(b, a, y=[2.])
>>> signal.lfilter(b, a, x, zi=zi)
(array([ 1.16666667,  0.63888889,  0.21296296,  0.07098765]), array([0.02366]))

Обратите внимание, что выходной сигнал \(y[n]\) имеет ту же длину, что и входной сигнал \(x[n]\).

Анализ линейных систем

Линейная система, описываемая линейным разностным уравнением, может быть полностью описана векторами коэффициентов \(a\) и \(b\) как было сделано выше; альтернативное представление - предоставить множитель \(k\), \(N_z\) zeros \(z_k\) и \(N_p\) полюса \(p_k\), соответственно, для описания системы с помощью её передаточной функции \(H(z)\), согласно

\[H(z) = k \frac{ (z-z_1)(z-z_2)...(z-z_{N_z})}{ (z-p_1)(z-p_2)...(z-p_{N_p})}.\]

Это альтернативное представление можно получить с помощью функции scipy tf2zpk; обратное значение предоставляется zpk2tf.

Для приведённого выше примера имеем

>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.tf2zpk(b, a)
(array([-0.5]), array([ 0.33333333]), 0.5)

т.е., система имеет ноль в \(z=-1/2\) и полюс в \(z=1/3\).

Функция scipy freqz позволяет рассчитать частотную характеристику системы, описанной коэффициентами \(a_k\) и \(b_k\). Смотрите справку для freqz функция для подробного примера.

Проектирование фильтров

Дискретные по времени фильтры можно классифицировать на фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ). КИХ-фильтры могут обеспечивать линейную фазовую характеристику, тогда как БИХ-фильтры не могут. SciPy предоставляет функции для проектирования обоих типов фильтров.

КИХ-фильтр

Функция firwin проектирует фильтры согласно методу окна. В зависимости от предоставленных аргументов функция возвращает различные типы фильтров (например, низкочастотные, полосовые…).

Пример ниже проектирует фильтр нижних частот и полосно-заграждающий фильтр соответственно.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b1 = signal.firwin(40, 0.5)
>>> b2 = signal.firwin(41, [0.3, 0.8])
>>> w1, h1 = signal.freqz(b1)
>>> w2, h2 = signal.freqz(b2)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w1, 20*np.log10(np.abs(h1)), 'b')
>>> plt.plot(w2, 20*np.log10(np.abs(h2)), 'r')
>>> plt.ylabel('Amplitude Response (dB)')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

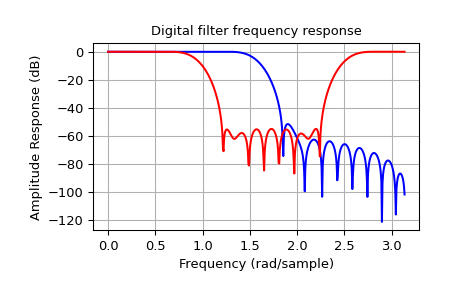
Обратите внимание, что firwin использует, по умолчанию, нормализованную частоту, определённую так, что значение \(1\) соответствует частоте Найквиста, тогда как функция freqz определяется таким образом, что значение \(\pi\) соответствует частоте Найквиста.

Функция firwin2 позволяет проектировать практически произвольные частотные характеристики, задавая массив граничных частот и соответствующих усилений, соответственно.

В примере ниже проектируется фильтр с такой произвольной амплитудной характеристикой.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b = signal.firwin2(150, [0.0, 0.3, 0.6, 1.0], [1.0, 2.0, 0.5, 0.0])
>>> w, h = signal.freqz(b)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, np.abs(h))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

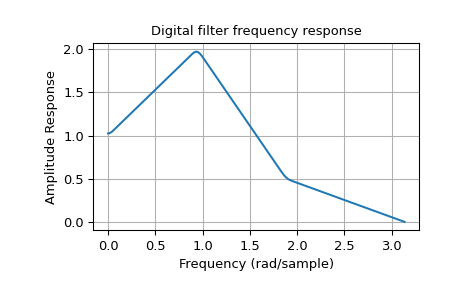
Обратите внимание на линейное масштабирование оси y и другое определение частоты Найквиста в firwin2 и freqz (как объяснено выше).

IIR фильтр

SciPy предоставляет две функции для непосредственного проектирования IIR iirdesign и iirfilter, где тип фильтра (например, эллиптический) передаётся как аргумент, и несколько дополнительных функций проектирования фильтров для конкретных типов фильтров, например, ellip.

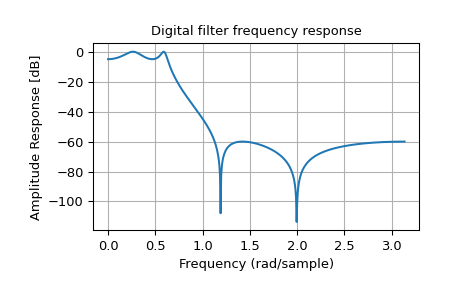
В примере ниже проектируется эллиптический фильтр нижних частот с определенной пульсацией в полосе пропускания и полосе задерживания соответственно. Обратите внимание на гораздо меньший порядок фильтра (порядок 4) по сравнению с КИХ-фильтрами из примеров выше, чтобы достичь того же затухания в полосе задерживания \(\approx 60\) дБ.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirfilter(4, Wn=0.2, rp=5, rs=60, btype='lowpass', ftype='ellip')
>>> w, h = signal.freqz(b, a)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

Примечание

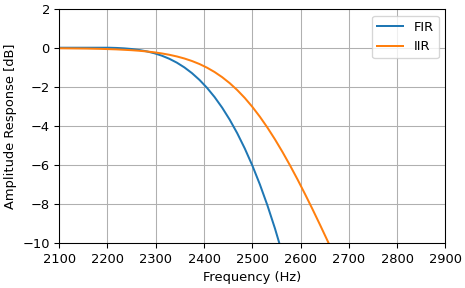
Важно отметить, что пороговые значения для firwin и iirfilter определяются по-разному. Для firwin, частота среза находится на половине амплитуды (т.е. -6 дБ). Для iirfilter, порог отсечения установлен на уровне половины мощности (т.е. -3дБ).

>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from scipy import signal as sig

>>> fs = 16000
>>> b = sig.firwin(101, 2500, fs=fs)
>>> f, h_fft = sig.freqz(b, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> _, ax = plt.subplots(layout="constrained")
>>> ax.plot(f, h_amp, label="FIR")
>>> ax.grid(True)

>>> b, a = sig.iirfilter(15, 2500, btype="low", fs=fs)
>>> f, h_fft = sig.freqz(b, a, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> ax.plot(f, h_amp, label="IIR")
>>> ax.set(xlim=[2100, 2900], ylim=[-10, 2])
>>> ax.set(xlabel="Frequency (Hz)", ylabel="Amplitude Response [dB]")
>>> ax.legend()

Коэффициенты фильтра

Коэффициенты фильтра могут храниться в нескольких различных форматах:

• ‘ba’ или ‘tf’ = коэффициенты передаточной функции

• 'zpk' = нули, полюсы и общий коэффициент усиления

• ‘ss’ = представление системы в пространстве состояний

• 'sos' = коэффициенты передаточной функции звеньев второго порядка

Функции, такие как tf2zpk и zpk2ss, может конвертировать между ними.

Представление передаточной функции

The ba или tf формат представляет собой кортеж из 2 элементов (b, a) представляющий передаточную функцию, где b имеет длину M+1 массив коэффициентов M-порядковый полином числителя, и a имеет длину N+1 массив коэффициентов N-го порядка знаменателя, как положительные, убывающие степени переменной передаточной функции. Таким образом, кортеж \(b = [b_0, b_1, ..., b_M]\) и \(a =[a_0, a_1, ..., a_N]\) может представлять аналоговый фильтр вида:

\[H(s) = \frac {b_0 s^M + b_1 s^{(M-1)} + \cdots + b_M} {a_0 s^N + a_1 s^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i s^{(M-i)}} {\sum_{i=0}^N a_i s^{(N-i)}}\]

или дискретно-временной фильтр вида:

\[H(z) = \frac {b_0 z^M + b_1 z^{(M-1)} + \cdots + b_M} {a_0 z^N + a_1 z^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i z^{(M-i)}} {\sum_{i=0}^N a_i z^{(N-i)}}.\]

Эта форма "положительных степеней" чаще встречается в технике управления. Если M и N равны (что верно для всех фильтров, сгенерированных билинейным преобразованием), то это оказывается эквивалентным форме с "отрицательными степенями" в дискретном времени, предпочитаемой в ЦОС:

\[H(z) = \frac {b_0 + b_1 z^{-1} + \cdots + b_M z^{-M}} {a_0 + a_1 z^{-1} + \cdots + a_N z^{-N}} = \frac {\sum_{i=0}^M b_i z^{-i}} {\sum_{i=0}^N a_i z^{-i}}.\]

Хотя это верно для обычных фильтров, помните, что это неверно в общем случае. Если M и N не равны, коэффициенты дискретно-временной передаточной функции должны сначала быть преобразованы в форму «положительных степеней» перед нахождением полюсов и нулей.

Это представление страдает от численной погрешности при более высоких порядках, поэтому другие форматы предпочтительны, когда это возможно.

Представление нулей и полюсов

The zpk формат представляет собой кортеж из 3 элементов (z, p, k), где z является M-массив длины комплексных нулей передаточной функции \(z = [z_0, z_1, ..., z_{M-1}]\), p является N-длинный массив комплексных полюсов передаточной функции \(p = [p_0, p_1, ..., p_{N-1}]\), и k является скалярным коэффициентом усиления. Они представляют цифровую передаточную функцию:

\[H(z) = k \cdot \frac {(z - z_0) (z - z_1) \cdots (z - z_{(M-1)})} {(z - p_0) (z - p_1) \cdots (z - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (z - z_i)} {\prod_{i=0}^{N-1} (z - p_i)}\]

или аналоговой передаточной функцией:

\[H(s) = k \cdot \frac {(s - z_0) (s - z_1) \cdots (s - z_{(M-1)})} {(s - p_0) (s - p_1) \cdots (s - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (s - z_i)} {\prod_{i=0}^{N-1} (s - p_i)}.\]

Хотя наборы корней хранятся как упорядоченные массивы NumPy, их порядок не имеет значения: ([-1, -2], [-3, -4], 1) является тем же фильтром, что и ([-2, -1], [-4, -3], 1).

Представление системы в пространстве состояний

The ss формат — это кортеж из 4 массивов (A, B, C, D) представляющий пространство состояний N-порядковая цифровая/дискретно-временная система вида:

\[\begin{split}\mathbf{x}[k+1] = A \mathbf{x}[k] + B \mathbf{u}[k]\\ \mathbf{y}[k] = C \mathbf{x}[k] + D \mathbf{u}[k]\end{split}\]

или непрерывная/аналоговая система вида:

\[\begin{split}\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)\\ \mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t),\end{split}\]

с P входные данные, Q выходы и N переменные состояния, где:

• x является вектором состояния

• y является выходным вектором длины Q

• u это входной вектор длины P

• A является матрицей состояния с формой (N, N)

• B является входной матрицей с формой (N, P)

• C является выходной матрицей с формой (Q, N)

• D является матрицей сквозной или прямой передачи с формой (Q, P). (В случаях, когда система не имеет прямого прохода, все значения в D равны нулю.)

Пространство состояний — это наиболее общее представление и единственное, которое позволяет использовать системы с несколькими входами и выходами (MIMO). Для заданной передаточной функции существует несколько представлений пространства состояний. В частности, «управляемая каноническая форма» и «наблюдаемая каноническая форма» имеют те же коэффициенты, что и tf представление и, следовательно, страдают от тех же численных ошибок.

Представление звеньев второго порядка

The sos формат - это один двумерный массив формы (n_sections, 6), представляющая последовательность передаточных функций второго порядка, которые, будучи соединены каскадно, реализуют фильтр более высокого порядка с минимальной числовой погрешностью. Каждая строка соответствует второму порядку tf представление, где первые три столбца предоставляют коэффициенты числителя, а последние три — коэффициенты знаменателя:

\[[b_0, b_1, b_2, a_0, a_1, a_2]\]

Коэффициенты обычно нормализуются так, что \(a_0\) всегда равно 1. Порядок секций обычно не важен при вычислениях с плавающей запятой; выход фильтра будет одинаковым независимо от порядка.

Фильтрующие преобразования

Функции проектирования IIR-фильтров сначала генерируют прототип аналогового фильтра нижних частот с нормированной частотой среза 1 рад/с. Затем он преобразуется в другие частоты и типы полос с использованием следующих подстановок:

Тип	Преобразование
lp2lp	\(s \rightarrow \frac{s}{\omega_0}\)
lp2hp	\(s \rightarrow \frac{\omega_0}{s}\)
lp2bp	\(s \rightarrow \frac{s^2 + {\omega_0}^2}{s \cdot \mathrm{BW}}\)
lp2bs	\(s \rightarrow \frac{s \cdot \mathrm{BW}}{s^2 + {\omega_0}^2}\)

Здесь, \(\omega_0\) является новой частотой среза или центральной частотой, и \(\mathrm{BW}\) это ширина полосы. Они сохраняют симметрию на логарифмической частотной оси.

Чтобы преобразовать преобразованный аналоговый фильтр в цифровой фильтр, bilinear используется преобразование, которое делает следующую замену:

\[s \rightarrow \frac{2}{T} \frac{z - 1}{z + 1},\]

где T - время выборки (обратное частоте дискретизации).

Другие фильтры

Пакет обработки сигналов предоставляет гораздо больше фильтров.

Медианный фильтр

Медианный фильтр обычно применяется, когда шум явно не гауссовский или когда требуется сохранить границы. Медианный фильтр работает, сортируя все значения пикселей массива в прямоугольной области, окружающей интересующую точку. Выборочная медиана этого списка значений соседних пикселей используется как значение для выходного массива. Выборочная медиана — это среднее значение массива в отсортированном списке значений соседей. Если в окрестности чётное количество элементов, то среднее двух средних значений используется как медиана. Универсальный медианный фильтр, работающий с N-мерными массивами, это medfilt. Специализированная версия, работающая только с двумерными массивами, доступна как medfilt2d.

Фильтр порядка

Медианный фильтр — это частный случай более общего класса фильтров, называемых порядковыми фильтрами. Для вычисления выходного значения в конкретном пикселе все порядковые фильтры используют значения массива в области вокруг этого пикселя. Эти значения массива сортируются, и затем одно из них выбирается в качестве выходного значения. Для медианного фильтра в качестве выхода используется выборочная медиана списка значений массива. Общий порядковый фильтр позволяет пользователю выбрать, какое из отсортированных значений будет использоваться в качестве выхода. Например, можно выбрать максимальное или минимальное значение в списке. Порядковый фильтр принимает дополнительный аргумент помимо входного массива и маски области, который указывает, какой элемент в отсортированном списке значений соседних массивов должен использоваться в качестве выхода. Команда для выполнения порядкового фильтра: order_filter.

Фильтр Винера

Фильтр Винера — это простой фильтр для устранения размытия и шума на изображениях. Это не фильтр Винера, обычно описываемый в задачах восстановления изображений, а простой локальный средний фильтр. Пусть \(x\) будет входным сигналом, тогда выходом является

\[\begin{split}y=\left\{ \begin{array}{cc} \frac{\sigma^{2}}{\sigma_{x}^{2}}m_{x}+\left(1-\frac{\sigma^{2}}{\sigma_{x}^{2}}\right)x & \sigma_{x}^{2}\geq\sigma^{2},\\ m_{x} & \sigma_{x}^{2}<\sigma^{2},\end{array}\right.\end{split}\]

где \(m_{x}\) является локальной оценкой среднего и \(\sigma_{x}^{2}\) является локальной оценкой дисперсии. Окно для этих оценок является необязательным входным параметром (по умолчанию \(3\times3\) ). Параметр \(\sigma^{2}\) является пороговым параметром шума. Если \(\sigma\) если не задано, то оценивается как среднее локальных дисперсий.

Фильтр Гильберта

Преобразование Гильберта строит комплекснозначный аналитический сигнал из вещественного сигнала. Например, если \(x=\cos\omega n\), затем \(y=\textrm{hilbert}\left(x\right)\) вернет (кроме краев) \(y=\exp\left(j\omega n\right).\) В частотной области, преобразование Гильберта выполняет

\[Y=X\cdot H,\]

где \(H\) является \(2\) для положительных частот, \(0\) для отрицательных частот, и \(1\) для нулевых частот.

Проектирование аналоговых фильтров

Функции iirdesign, iirfilter, и функции проектирования фильтров для конкретных типов фильтров (например, ellip) все имеют флаг аналог, что позволяет проектировать аналоговые фильтры.

В примере ниже проектируется аналоговый (IIR) фильтр, получается через tf2zpk полюса и нули и отображает их в комплексной s-плоскости. Нули в \(\omega \approx 150\) и \(\omega \approx 300\) можно чётко увидеть в амплитудной характеристике.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirdesign(wp=100, ws=200, gpass=2.0, gstop=40., analog=True)
>>> w, h = signal.freqs(b, a)

>>> plt.title('Analog filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency')
>>> plt.grid()
>>> plt.show()

>>> z, p, k = signal.tf2zpk(b, a)

>>> plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
>>> plt.plot(np.real(p), np.imag(p), 'xr')
>>> plt.legend(['Zeros', 'Poles'], loc=2)

>>> plt.title('Pole / Zero Plot')
>>> plt.xlabel('Real')
>>> plt.ylabel('Imaginary')
>>> plt.grid()
>>> plt.show()

\[% LaTeX Macros to make the LaTeX formulas more readable: \newcommand{\IC}{{\mathbb{C}}} % set of complex numbers \newcommand{\IN}{{\mathbb{N}}} % set of natural numbers \newcommand{\IR}{{\mathbb{R}}} % set of real numbers \newcommand{\IZ}{{\mathbb{Z}}} % set of integers \newcommand{\jj}{{\mathbb{j}}} % imaginary unit \newcommand{\e}{\operatorname{e}} % Euler's number \newcommand{\dd}{\operatorname{d}} % infinitesimal operator \newcommand{\abs}[1]{\left|#1\right|} % absolute value \newcommand{\conj}[1]{\overline{#1}} % complex conjugate \newcommand{\conjT}[1]{\overline{#1^T}} % transposed complex conjugate \newcommand{\inv}[1]{\left(#1\right)^{\!-1}} % inverse % Since the physics package is not loaded, we define the macros ourselves: \newcommand{\vb}[1]{\mathbf{#1}} % vectors and matrices are bold % new macros: \newcommand{\rect}{\operatorname{rect}} % rect or boxcar function \newcommand{\sinc}{\operatorname{sinc}} % sinc(t) := sin(pi*t) / (pi*t)\]

Спектральный анализ

Спектральный анализ относится к исследованию преобразования Фурье [1] сигнала. В зависимости от контекста, различные названия, такие как спектр, спектральная плотность или периодограмма, существуют для различных спектральных представлений преобразования Фурье. [2] Этот раздел иллюстрирует наиболее распространённые представления на примере сигнала синусоидальной волны непрерывного времени фиксированной длительности. Затем использование дискретного преобразования Фурье [3] обсуждается на выборке этой синусоидальной волны.

Отдельные подразделы посвящены фазе спектра, оценке спектральной плотности мощности без (periodogram. Это сложная реализация, которая должна занимать примерно 3/8 времени наивной реализации. Асимптотика одинакова.welch) также для неравномерно распределённых сигналов (lombscargle).

Обратите внимание, что концепция ряда Фурье тесно связана, но отличается в ключевом аспекте: ряды Фурье имеют спектр, состоящий из гармоник с дискретными частотами, тогда как в этом разделе спектры непрерывны по частоте.

Синусоидальный сигнал непрерывного времени

Рассмотрим синусоидальный сигнал с амплитудой \(a\), частота \(f_x\) и длительностью \(\tau\), т.е.,

(1)\[x(t) = a \sin(2 \pi f_x t)\, \rect(\frac{t}{\tau}-\frac{1}{2}) = \left(\frac{a}{2\jj} \e^{\jj 2 \pi f_x t} - \frac{a}{2\jj} \e^{-\jj 2 \pi f_x t} \right) \rect(\frac{t}{\tau}-\frac{1}{2})\ .\]

Поскольку \(\rect(t)\) функция равна единице для \(|t|<1/2\) и ноль для \(|t|>1/2\), это ограничивает \(x(t)\) в интервал \([0, \tau]\). Выражение синуса через комплексные экспоненты показывает его две периодические компоненты с частотами \(\pm f_x\). Мы предполагаем \(x(t)\) быть сигналом напряжения, поэтому имеет единицу измерения \(\text{V}\).

В обработке сигналов интеграл от квадрата модуля \(|x(t)|^2\) используется для определения энергии и мощности сигнала, т.е.,

(2)\[E_x := \int_0^\tau |x(t)|^2 \dd t\ = \frac{1}{2}|a|^2\tau\ , \qquad P_x := \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ .\]

Степень \(P_x\) может интерпретироваться как энергия \(E_x\) за единицу времени интервала. С точки зрения единиц измерения, интегрирование по \(t\) приводит к умножению на секунды. Следовательно, \(E_x\) имеет единицу измерения \(\text{V}^2\text{s}\) и \(P_x\) имеет единицу измерения \(\text{V}^2\).

Применяя преобразование Фурье к \(x(t)\), т.е.,

(3)\[X(f) = \int_{\IR} x(t)\, \e^{-2\jj\pi f t}\, \dd t = \frac{a \tau}{2\jj} \Big( \sinc\!\big(\tau (f-f_x)\big) - \sinc\!\big(\tau (f+f_x)\big) \Big)\e^{-\jj\pi\tau f}\ ,\]

приводит к двум \(\sinc(f) := \sin(\pi f) /(\pi f)\) функции, центрированные в \(\pm f_x\). Величина (абсолютное значение) \(|X(f)|\) имеет два максимума, расположенных в \(\pm f_x\) со значением \(|a|\tau/2\). На графике ниже видно, что \(X(f)\) не сконцентрирован вокруг главных лепестков на \(\pm f_x\), но содержит боковые лепестки с высотами, уменьшающимися пропорционально \(1/(\tau f)\). Этот так называемый "спектральный пролив" [4] вызвано ограничением синуса конечным интервалом. Заметьте, что чем короче длительность сигнала \(\tau\) чем выше, тем больше утечка. Чтобы быть независимым от длительности сигнала, так называемый «амплитудный спектр» \(X(f)/\tau\) может использоваться вместо спектра \(X(f)\). Его значение в \(f\) соответствует амплитуде комплексной экспоненты \(\exp(\jj2\pi f t)\).

Благодаря теореме Парсеваля, энергию можно вычислить из её преобразования Фурье \(X(f)\) by

(4)\[ E_X := \int_\IR \abs{X(f)}^2 \dd f = E_x\]

также. Например, прямым вычислением можно показать, что энергия \(X(f)\) уравнения (4) является \(|a|^2\tau/2\). Следовательно, мощность сигнала в частотной полосе \([f_a, f_b]\) может быть определён с помощью

(5)\[P_X^{a,b} = \frac{1}{\tau} \int_{f_a}^{f_b} \abs{X(f)}^2 \dd f\ .\]

Таким образом, функция \(|X(f)|^2\) может быть определена как так называемая «спектральная плотность энергии и \(S_{xx}(f) := |X(f)|^2 / \tau\) как "спектральная плотность мощности" (PSD) от \(x(t)\). Вместо PSD, так называемая «спектральная плотность амплитуды» \(X(f) / \sqrt{\tau}\) также используется, который все еще содержит информацию о фазе. Его абсолютный квадрат - это СПМ, и поэтому он тесно связан с концепцией среднеквадратичного (RMS) значения \(\sqrt{P_x}\) сигнала.

В итоге, в этом подразделе представлены пять способов представления спектра:

Сравнение спектральных представлений синусоидального сигнала \(x(t)\) уравнения (1) с единицей \(\text{V}\):

	Спектр	Амплитудный спектр	Спектральная плотность энергии	Спектральная плотность мощности (PSD)	Амплитудная спектральная плотность
Определение:	\(X(f)\)	\(X(f) / \tau\)	\(|X(f)|^2\)	\(|X(f)|^2 / \tau\)	\(X(f) / \sqrt{\tau}\)
Величина на \(\pm f_x\):	\(\frac{1}{2}|a|\tau\)	\(\frac{1}{2}|a|\)	\(\frac{1}{4}|a|^2\tau^2\)	\(\frac{1}{4}|a|^2\tau\)	\(\frac{1}{2}|a|\sqrt{\tau}\)
Единица измерения:	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

Обратите внимание, что единицы измерения, представленные в таблице выше, неоднозначны, например, \(\text{V}^2\text{s} / \text{Hz} = \text{V}^2\text{s}^2 = \text{V}^2/ \text{Hz}^2\). При использовании абсолютного значения \(|X(f) / \tau|\) амплитудного спектра, он называется спектром амплитуд. Кроме того, обратите внимание, что схема именования представлений не является последовательной и варьируется в литературе.

Для вещественных сигналов часто используется так называемое «одностороннее» спектральное представление. Оно использует только неотрицательные частоты (из-за \(X(-f)= \conj{X}(f)\) if \(x(t)\in\IR\)). Иногда значения отрицательных частот добавляются к их положительным аналогам. Тогда амплитудный спектр позволяет считать полную (не половинную) амплитуду синуса \(x(t)\) в \(f_x\) и площадь интервала в PSD представляет его полную (не половину) мощность. Обратите внимание, что для амплитудных спектральных плотностей положительные значения не удваиваются, а умножаются на \(\sqrt{2}\), поскольку это квадратный корень из PSD. Кроме того, нет канонического способа именования удвоенного спектра.

Следующий график показывает три различных спектральных представления четырёх синусоидальных сигналов \(x(t)\) уравнения (1) с разными амплитудами \(a\) и длительности \(\tau\). Для меньшей загроможденности спектры центрированы на \(f_x\) и находятся рядом друг с другом:

import matplotlib.pyplot as plt
import numpy as np

aa = [1, 1, 2, 2]  # amplitudes
taus = [1, 2, 1, 2]  # durations

fg0, axx = plt.subplots(3, 1, sharex='all', tight_layout=True, figsize=(6., 4.))
axx[0].set(title=r"Spectrum $|X(f)|$", ylabel="V/Hz")
axx[1].set(title=r"Magnitude Spectrum $|X(f)/\tau|$ ", ylabel=r"V")
axx[2].set(title=r"Amplitude Spectral Density $|X(f)/\sqrt{\tau}|$",
           ylabel=r"$\operatorname{V} / \sqrt{\operatorname{Hz}}$",
           xlabel="Frequency $f$ in Hertz",)

x_labels, x_ticks = [], []
f = np.linspace(-2.5, 2.5, 400)
for c_, (a_, tau_) in enumerate(zip(aa, taus), start=1):
    aZ_, f_ = abs(a_ * tau_ * np.sinc(tau_ * f) / 2), f + c_ * 5
    axx[0].plot(f_, aZ_)
    axx[1].plot(f_, aZ_ / tau_)
    axx[2].plot(f_, aZ_ / np.sqrt(tau_))
    x_labels.append(rf"$a={a_:g}$, $\tau={tau_:g}$")
    x_ticks.append(c_ * 5)

axx[2].set_xticks(x_ticks)
axx[2].set_xticklabels(x_labels)
plt.show()

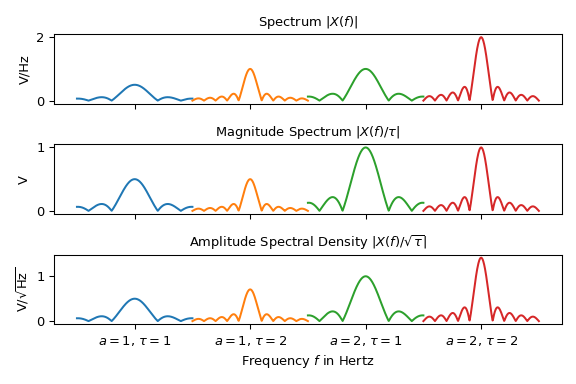
Обратите внимание, что в зависимости от представления высота пиков может различаться. Только интерпретация амплитудного спектра является однозначной: пик на \(f_x\) во втором графике представляет половину амплитуды \(|a|\) синусоидального сигнала. Для всех других представлений длительность \(\tau\) необходимо учитывать для извлечения информации об амплитуде сигнала.

Дискретизированный синусоидальный сигнал

На практике широко используются дискретизированные сигналы. Т.е. сигнал представлен \(n\) образцы \(x_k := x(kT)\), \(k=0, \ldots, n-1\), где \(T\) является интервалом дискретизации, \(\tau:=nT\) длительность сигнала и \(f_S := 1/T\) частота дискретизации. Обратите внимание, что непрерывный сигнал должен быть ограничен по полосе до \([-f_S/2, f_S/2]\) чтобы избежать алиасинга, с \(f_S/2\) называется частотой Найквиста. [5] Заменяя интеграл суммой для вычисления энергии и мощности сигнала, т.е.,

\[E_x = T\sum_{k=0}^{n-1} \abs{x_k}^2 = \frac{1}{2}|a|^2\tau\ , \qquad P_x = \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ ,\]

даёт идентичный результат, как в непрерывном случае уравнения (2). Дискретное преобразование Фурье (ДПФ) и его обратное (реализованное с использованием эффективных вычислений БПФ в scipy.fft модуля) задается

(6)\[X_l := \sum_{k=0}^{n-1} x_k \e^{-2\jj\pi k l / n}\ ,\qquad x_k = \frac{1}{n} \sum_{l=0}^{n-1} X_l \e^{2\jj\pi k l / n}\ .\]

ДПФ и может интерпретироваться как немасштабированная дискретизированная версия непрерывного преобразования Фурье из уравнения. (3), т.е.,

\[X(l\Delta f) = T X_l\ , \quad \Delta f := 1/\tau = 1/(nT)\ .\]

Следующий график показывает амплитудный спектр двух синусоидальных сигналов с единичной амплитудой и частотами 20 Гц и 20,5 Гц. Сигнал состоит из \(n=100\) выборки с интервалом выборки \(T=10\) мс, что приводит к длительности \(\tau=1\) с и частотой дискретизации \(f_S=100\) Гц.

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
fcc = (20, 20.5)  # frequencies of sines
t = np.arange(n) * T
xx = (np.sin(2 * np.pi * fx_ * t) for fx_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided magnitude spectrum

fg1, ax1 = plt.subplots(1, 1, tight_layout=True, figsize=(6., 3.))
ax1.set(title=r"Magnitude Spectrum (no window) of $x(t) = \sin(2\pi f_x t)$ ",
        xlabel=rf"Frequency $f$ in Hertz (bin width $\Delta f = {f[1]}\,$Hz)",
        ylabel=r"Magnitude $|X(f)|/\tau$", xlim=(f[0], f[-1]))
for X_, fc_, m_ in zip(XX, fcc, ('x-', '.-')):
    ax1.plot(f, abs(X_), m_, label=rf"$f_x={fc_}\,$Hz")

ax1.grid(True)
ax1.legend()
plt.show()

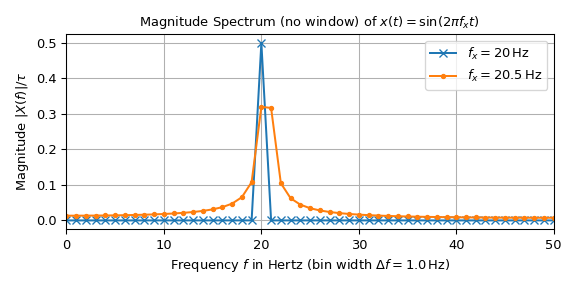
Интерпретация сигнала 20 Гц кажется простой: все значения равны нулю, кроме 20 Гц. Там оно равно 0.5, что соответствует половине амплитуды входного сигнала в соответствии с уравнением. (1). Пик сигнала 20.5 Гц с другой стороны рассеян вдоль оси частот. Ур. (3) показывает, что эта разница вызвана тем, что 20 Гц кратно ширине бина 1 Гц, тогда как 20.5 Гц — нет. Следующий график иллюстрирует это, накладывая непрерывный спектр на дискретизированный:

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = (np.sin(2 * np.pi * fc_ * t) for fc_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided FFT normalized to magnitude

i0, i1 = 15, 25
f_cont = np.linspace(f[i0], f[i1], 501)

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, fx_) in enumerate(zip(axx, XX, fcc)):
    Xc_ = (np.sinc(tau * (f_cont - fx_)) +
           np.sinc(tau * (f_cont + fx_))) / 2
    ax_.plot(f_cont, abs(Xc_), f'-C{c_}', alpha=.5, label=rf"$f_x={fx_}\,$Hz")
    m_line, _, _, = ax_.stem(f[i0:i1+1], abs(X_[i0:i1+1]), markerfmt=f'dC{c_}',
                             linefmt=f'-C{c_}', basefmt=' ')
    plt.setp(m_line, markersize=5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f[i0], f[i1]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle("Continuous and Sampled Magnitude Spectrum ", x=0.55, y=0.93)
fg1.tight_layout()
plt.show()

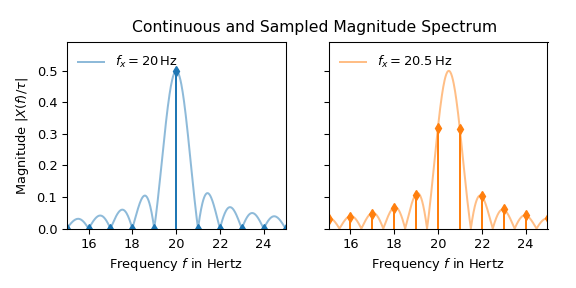
То, что небольшое изменение частоты приводит к значительно отличающимся спектрам амплитуд, очевидно, является нежелательным поведением для многих практических приложений. Следующие две распространённые техники могут быть использованы для улучшения спектра:

Так называемое "дополнение нулями" уменьшает \(\Delta f\) путем добавления нулей в конец сигнала. Для передискретизации частоты q раз, передайте параметр n=q*n_x к fft / rfft функция с n_x является длиной входного сигнала.

Вторая техника называется оконным преобразованием, т.е. умножением входного сигнала на подходящую функцию, так что обычно боковые лепестки подавляются за счёт расширения главного лепестка. Оконное ДПФ можно выразить как

(7)\[X^w_l := \sum_{k=0}^{n-1} x_k w_k\e^{-2\jj\pi k l / n}\ ,\]

где \(w_k\), \(k=0,\ldots,n-1\) является дискретизированной оконной функцией. Для вычисления дискретизированных версий спектральных представлений, приведённых в предыдущем подразделе, используются следующие нормировочные константы

\[c^\text{amp}:= \abs{\sum_{k=0}^{n-1} w_k}\ ,\qquad c^\text{den} := \sqrt{\sum_{k=0}^{n-1} \abs{w_k}^2}\]

должны быть использованы. Первая гарантирует, что пик в спектре соответствует амплитуде сигнала на этой частоте. Например, амплитудный спектр может быть выражен как \(|X^w_l / c^\text{amp}|\). Вторая константа гарантирует, что мощность частотного интервала, как определено в уравнении (5) является согласованной. Абсолютные значения необходимы, поскольку комплекснозначные окна не запрещены.

Следующий график показывает результат применения hann окно и трехкратное передискретизация для \(x(t)\):

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal.windows import hann

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
q = 3  # over-sampling factor
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = [np.sin(2 * np.pi * fc_ * t) for fc_ in fcc]  # sine signals
w = hann(n)
c_w = abs(sum(w))  # normalize constant for window

f_X = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_ * w) / c_w for x_ in xx)  # one-sided amplitude spectrum
# Oversampled spectrum:
f_Y = rfftfreq(n*q, T)  # frequency bins range from 0 Hz to Nyquist freq.
YY = (rfft(x_ * w, n=q*n) / c_w for x_ in xx)  # one-sided magnitude spectrum

i0, i1 = 15, 25
j0, j1 = i0*q, i1*q

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, Y_, fx_) in enumerate(zip(axx, XX, YY, fcc)):
    ax_.plot(f_Y[j0:j1 + 1], abs(Y_[j0:j1 + 1]), f'.-C{c_}',
             label=rf"$f_x={fx_}\,$Hz")
    m_ln, s_ln, _, = ax_.stem(f_X[i0:i1 + 1], abs(X_[i0:i1 + 1]), basefmt=' ',
                              markerfmt=f'dC{c_}', linefmt=f'-C{c_}')
    plt.setp(m_ln, markersize=5)
    plt.setp(s_ln, alpha=0.5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f_X[15], f_X[25]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle(rf"Magnitude Spectrum (Hann window, ${q}\times$oversampled)",
             x=0.55, y=0.93)
plt.show()

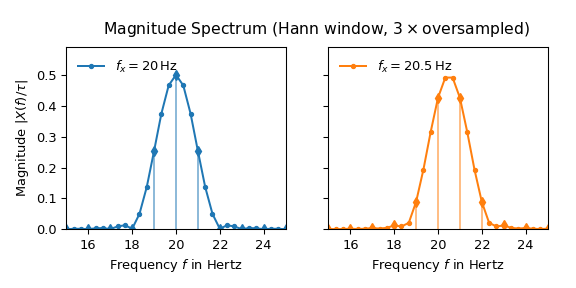
Теперь обе доли выглядят почти идентично, а боковые доли хорошо подавлены. Максимум спектра 20.5 Гц также очень близок к ожидаемой высоте в половину.

Спектральная энергия и спектральная мощность могут быть рассчитаны аналогично уравнению. (4), давая идентичные результаты, т.е.,

\[E^w_X = T\sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = E_x\ ,\qquad P^w_X = \frac{1}{\tau} E^w_X = \frac{1}{n} \sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = P_x\ .\]

Эта формулировка не должна путаться с частным случаем прямоугольного окна (или отсутствия окна), т.е., \(w_k = 1\), \(X^w_l=X_l\), \(c^\text{den}=\sqrt{n}\), что приводит к

\[E_X = \frac{T}{n}\sum_{k=0}^{n-1} \abs{X_k}^2\ ,\qquad P_X = \frac{1}{n^2} \sum_{k=0}^{n-1} \abs{X_k}^2\ .\]

Оконная частотно-дискретная спектральная плотность мощности

\[S^w_{xx} := \frac{1}{f_S}\abs{\frac{X^w_l}{c^\text{den}}}^2 = T \abs{\frac{X^w_l}{c^\text{den}}}^2\]

определена в диапазоне частот \([0, f_S)\) и может интерпретироваться как мощность на интервал частоты \(\Delta f\). Интегрирование по частотной полосе \([l_a\Delta f, l_b\Delta f)\), как в уравнении. (5), становится суммой

\[P_X^{a,b} = \Delta f\sum_{k=l_a}^{l_b-1} S^w_{xx} = \frac{1}{nT}\sum_{k=l_a}^{l_b-1} S^w_{xx}\ .\]

Оконная частотно-дискретная спектральная плотность энергии \(\tau S^w_{xx}\) может быть определён аналогично.

Обсуждение выше показывает, что дискретизированные версии спектральных представлений, как в непрерывном случае, могут быть определены. Следующая таблица суммирует их:

Сравнение спектральных представлений оконного ДПФ \(X^w_l\) уравнения (7) для дискретизированного сигнала с единичной \(\text{V}\):

	Спектр	Амплитудный спектр	Спектральная плотность энергии	Спектральная плотность мощности (PSD)	Амплитудная спектральная плотность
Определение:	\(\tau X^w_l / c^\text{amp}\)	\(X^w_l / c^\text{amp}\)	\(\tau T |X^w_l / c^\text{den}|^2\)	\(T |X^w_l / c^\text{den}|^2\)	\(\sqrt{T} X^w_l / c^\text{den}\)
Единица измерения:	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

Обратите внимание, что для плотностей величины значений в \(\pm f_x\) отличаются от случая непрерывного времени из-за замены интегрирования на суммирование для определения спектральной энергии/мощности.

Хотя окно Ханна является наиболее распространённой оконной функцией в спектральном анализе, существуют и другие окна. Следующий график показывает амплитудный спектр различных оконных функций для windows подмодуль. Может интерпретироваться как форма лепестка одиночного частотного входного сигнала. Заметим, что показана только правая половина и \(y\)-ось в децибелах, т.е. имеет логарифмический масштаб.

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal import get_window

n, n_zp = 128, 16384  # number of samples without and with zero-padding
t = np.arange(n)
f = rfftfreq(n_zp, 1 / n)

ww = ['boxcar', 'hann', 'hamming', 'tukey', 'blackman', 'flattop']
fg0, axx = plt.subplots(len(ww), 1, sharex='all', sharey='all', figsize=(6., 4.))
for c_, (w_name_, ax_) in enumerate(zip(ww, axx)):
    w_ = get_window(w_name_, n, fftbins=False)
    W_ = rfft(w_ / abs(sum(w_)), n=n_zp)
    W_dB = 20*np.log10(np.maximum(abs(W_), 1e-250))
    ax_.plot(f, W_dB, f'C{c_}-', label=w_name_)
    ax_.text(0.1, -50, w_name_, color=f'C{c_}', verticalalignment='bottom',
             horizontalalignment='left', bbox={'color': 'white', 'pad': 0})
    ax_.set_yticks([-20, -60])
    ax_.grid(axis='x')

axx[0].set_title("Spectral Leakage of various Windows")
fg0.supylabel(r"Normalized Magnitude $20\,\log_{10}|W(f)/c^\operatorname{amp}|$ in dB",
              x=0.04, y=0.5, fontsize='medium')
axx[-1].set(xlabel=r"Normalized frequency $f/\Delta f$ in bins",
            xlim=(0, 9), ylim=(-75, 3))

fg0.tight_layout(h_pad=0.4)
plt.show()

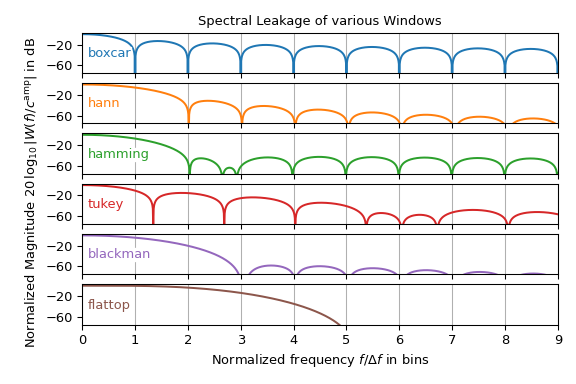
Этот график показывает, что выбор оконной функции обычно представляет собой компромисс между шириной главных лепестков и высотой боковых лепестков. Обратите внимание, что boxcar окно соответствует \(\rect\) функция, то есть без оконной обработки. Кроме того, многие из изображенных окон чаще используются при проектировании фильтров, чем в спектральном анализе.

Фаза спектра

Фаза (т.е., angle) преобразования Фурье обычно используется для исследования временной задержки спектральных компонент сигнала, проходящего через систему, такую как фильтр. В следующем примере стандартный тестовый сигнал, импульс с единичной мощностью, проходит через простой фильтр, который задерживает вход на три сэмпла. Вход состоит из \(n=50\) выборки с интервалом выборки \(T = 1\) s. График показывает амплитуду и фазу по частоте входного и выходного сигнала:

import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np

from scipy import signal
from scipy.fft import rfft, rfftfreq

# Create input signal:
n = 50
x = np.zeros(n)
x[0] = n

# Apply FIR filter which delays signal by 3 samples:
y = signal.lfilter([0, 0, 0, 1], 1, x)

X, Y = (rfft(z_) / n for z_ in (x, y))
f = rfftfreq(n, 1)  # sampling interval T = 1 s

fig = plt.figure(tight_layout=True, figsize=(6., 4.))
gs = gridspec.GridSpec(3, 1)
ax0 = fig.add_subplot(gs[0, :])
ax1 = fig.add_subplot(gs[1:, :], sharex=ax0)

for Z_, n_, m_ in zip((X, Y), ("Input $X(f)$", "Output $Y(f)$"), ('+-', 'x-')):
    ax0.plot(f, abs(Z_), m_, alpha=.5, label=n_)
    ax1.plot(f, np.unwrap(np.angle(Z_)), m_, alpha=.5, label=n_)

ax0.set(title="Frequency Response of 3 Sample Delay Filter (no window)",
        ylabel="Magnitude", xlim=(0, f[-1]), ylim=(0, 1.1))
ax1.set(xlabel=rf"Frequency $f$ in Hertz ($\Delta f = {1/n}\,$Hz)",
        ylabel=r"Phase in rad")
ax1.set_yticks(-np.arange(0, 7)*np.pi/2,
               ['0', '-π/2', '-π', '-3/2π', '-2π', '-4/3π', '-3π'])

ax2 = ax1.twinx()
ax2.set(ylabel=r"Phase in Degrees", ylim=np.rad2deg(ax1.get_ylim()),
        yticks=np.arange(-540, 90, 90))
for ax_ in (ax0, ax1):
    ax_.legend()
    ax_.grid()
plt.show()

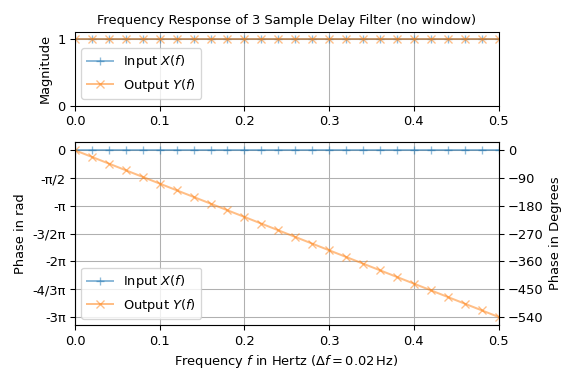
Входной сигнал имеет единичную амплитуду и нулевую фазу преобразования Фурье, что объясняет его использование в качестве тестового сигнала. Выходной сигнал также имеет единичную амплитуду, но линейно спадающую фазу с наклоном \(-6\pi\). Это ожидаемо, поскольку задержка сигнала \(x(t)\) by \(\Delta t\) создает дополнительный линейный фазовый член в своем преобразовании Фурье, т.е.,

\[\int_\IR x(t-\Delta t) \e^{-\jj2\pi f t}\dd t = X(f)\, e^{-\jj2\pi \Delta t f}\ .\]

Обратите внимание, что на графике фаза не ограничена интервалом \((+\pi, \pi]\) (вывод angle) и, следовательно, не имеет разрывов. Это достигается за счёт использования numpy.unwrap функция. Если передаточная функция фильтра известна, freqz может использоваться для непосредственного определения спектрального отклика фильтра.

Спектры с усреднением

The periodogram функция вычисляет спектральную плотность мощности (scaling='density') или спектр квадрата амплитуды (scaling='spectrum'). Для получения сглаженной периодограммы, welch функция может быть использована. Она выполняет сглаживание, разделяя входной сигнал на перекрывающиеся сегменты, чтобы затем вычислить оконное ДПФ каждого сегмента. Результат является средним значением этих ДПФ.

Пример ниже показывает квадрат амплитудного спектра и спектральную плотность мощности сигнала, состоящего из \(1.27\,\text{kHz}\) синусоидальный сигнал с амплитудой \(\sqrt{2}\,\text{V}\) и аддитивный гауссов шум со спектральной плотностью мощности со средним значением \(10^{-3}\,\text{V}^2/\text{Hz}\).

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal

rng = np.random.default_rng(73625)  # seeding for reproducibility

fs, n = 10e3, 10_000
f_x, noise_power = 1270, 1e-3 * fs / 2
t = np.arange(n) / fs
x = (np.sqrt(2) * np.sin(2 * np.pi * f_x * t) +
     rng.normal(scale=np.sqrt(noise_power), size=t.shape))

fg, axx = plt.subplots(1, 2, sharex='all', tight_layout=True, figsize=(7, 3.5))
axx[0].set(title="Squared Magnitude Spectrum", ylabel="Square of Magnitude in V²")
axx[1].set(title="Power Spectral Density", ylabel="Power Spectral Density in V²/Hz")
for ax_, s_ in zip(axx, ('spectrum', 'density')):
    f_p, P_p = signal.periodogram(x, fs, 'hann', scaling=s_)
    f_w, P_w = signal.welch(x, fs, scaling=s_)
    ax_.semilogy(f_p/1e3, P_p, label=f"Periodogram ({len(f_p)} bins)")
    ax_.semilogy(f_w/1e3, P_w, label=f"Welch's Method ({len(f_w)} bins)")
    ax_.set(xlabel="Frequency in kHz", xlim=(0, 2), ylim=(1e-7, 1.3))
    ax_.grid(True)
    ax_.legend(loc='lower center')
plt.show()

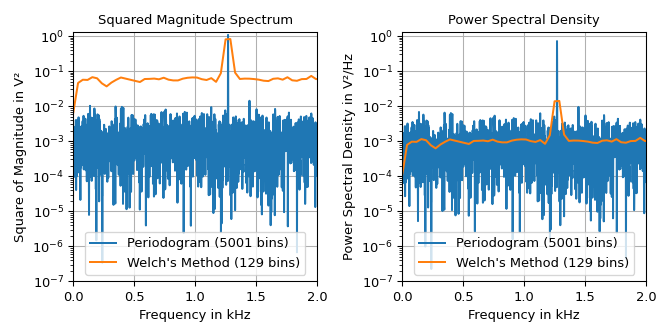
Графики показывают, что welch функция создаёт гораздо более гладкий шумовой пол на частоте за счёт разрешения по частоте. Из-за сглаживания высота лепестка синуса шире и не такая высокая, как в периодограмме. Левый график можно использовать для чтения высоты лепестка, т.е., половины квадрата амплитуды синуса \(1\,\text{V}^2\). Правый график можно использовать для определения уровня шума \(10^{-3}\,\text{V}^2/\text{Hz}\). Обратите внимание, что высота лепестка усредненного квадрата спектральной величины не равна точно единице из-за ограниченного частотного разрешения. Либо дополнение нулями (например, передача nfft=4*len(x) to welch) или уменьшение количества сегментов путем увеличения длины сегмента (установка параметра nperseg) может быть использован для увеличения количества частотных бинов.

Периодограммы Ломба-Скаргла (lombscargle)

Спектральный анализ методом наименьших квадратов (LSSA) [6] [7] является методом оценки частотного спектра, основанным на методе наименьших квадратов для подбора синусоид к выборкам данных, аналогично анализу Фурье. Анализ Фурье, наиболее используемый спектральный метод в науке, обычно усиливает долгопериодический шум в записях с большими пропусками; LSSA смягчает такие проблемы.

Метод Ломба-Скаргла выполняет спектральный анализ неравномерно дискретизированных данных и известен как мощный способ обнаружения и проверки значимости слабых периодических сигналов.

Для временного ряда, включающего \(N_{t}\) измерения \(X_{j}\equiv X(t_{j})\) выборка во времени \(t_{j}\), где \((j = 1, \ldots, N_{t})\), предполагается, что она масштабирована и сдвинута так, что ее среднее значение равно нулю, а дисперсия равна единице, нормированный периодограмм Ломба-Скаргла на частоте \(f\) является

\[P_{n}(f) = \frac{1}{2}\left\{\frac{\left[\sum_{j}^{N_{t}}X_{j}\cos\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\cos^{2}\omega(t_{j}-\tau)}+\frac{\left[\sum_{j}^{N_{t}}X_{j}\sin\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\sin^{2}\omega(t_{j}-\tau)}\right\}.\]

Здесь, \(\omega \equiv 2\pi f\) является угловой частотой. Частотно-зависимый временной сдвиг \(\tau\) задается формулой

\[\tan 2\omega\tau = \frac{\sum_{j}^{N_{t}}\sin 2\omega t_{j}}{\sum_{j}^{N_{t}}\cos 2\omega t_{j}}.\]

The lombscargle функция вычисляет периодограмму, используя слегка модифицированный алгоритм, созданный Цехмейстером и Кюрстером [8], что позволяет взвешивать отдельные выборки и вычислять неизвестное смещение (также называемое "плавающим средним") для каждой частоты независимо.

Кратковременное преобразование Фурье

В этом разделе представлена некоторая справочная информация по использованию ShortTimeFFT класс: Кратковременное преобразование Фурье (STFT) может использоваться для анализа спектральных свойств сигналов во времени. Оно разделяет сигнал на перекрывающиеся фрагменты с помощью скользящего окна и вычисляет преобразование Фурье каждого фрагмента. Для непрерывного комплекснозначного сигнала \(x(t)\) STFT определяется как [9] как

\[S(f, t) := \int_\IR x(\xi)\, \conj{w(\xi-t)}\,\e^{-\jj2\pi f \xi}\dd\xi\ ,\]

где \(w(t)\) является комплекснозначной оконной функцией, комплексно сопряжённая которой \(\conj{w(t)}\). Его можно интерпретировать как определение скалярного произведения \(x\) с окном \(w\) который переводится временем \(t\) а затем модулируется (т.е., сдвигается по частоте) частотой \(f\). Для работы с дискретизированными сигналами \(x[k] := x(kT)\), \(k\in\IZ\)с интервалом выборки \(T\) (являясь обратной величиной частоты дискретизации fs), дискретная версия, т.е. оценка STFT только в дискретных точках сетки \(S[q, p] := S(q \Delta f, p\Delta t)\), \(q,p\in\IZ\), необходимо использовать. Это можно сформулировать как

(8)\[S[q,p] = \sum_{k=0}^{N-1} x[k]\,\conj{w[k-p h]}\, \e^{-\jj2\pi q k / N}\ , \quad q,p\in\IZ\ ,\]

с p представляющий временной индекс \(S\) с временным интервалом \(\Delta t := h T\), \(h\in\IN\) (см. delta_t), который может быть выражен как hop размер \(h\) выборки. \(q\) представляет индекс частоты \(S\) с шагом \(\Delta f := 1 / (N T)\) (см. delta_f), что делает его совместимым с БПФ. \(w[m] := w(mT)\), \(m\in\IZ\) является дискретизированной оконной функцией.

Для большего соответствия реализации ShortTimeFFT, имеет смысл переформулировать уравнение. : TST: исправить некорректные тесты signal.sosfilt как двухэтапный процесс:

1. Извлечь \(p\)-й срез путём оконного преобразования с окном \(w[m]\) состоящий из \(M\) образцы (см. m_num) с центром в \(t[p] := p \Delta t = h T\) (см. delta_t), т.е.,

   (9)\[x_p[m] = x\!\big[m - \lfloor M/2\rfloor + h p\big]\, \conj{w[m]}\ , \quad m = 0, \ldots M-1\ ,\]

   где целое число \(\lfloor M/2\rfloor\) представляет M//2, т.е., это середина окна (m_num_mid). Для удобства обозначений, \(x[k]:=0\) для \(k\not\in\{0, 1, \ldots, N-1\}\) предполагается. В подразделе Скользящие окна индексирование срезов обсуждается более подробно.

2. Затем выполнить дискретное преобразование Фурье (т.е., БПФ) из \(x_p[m]\).

   (10)\[S[q, p] = \sum_{m=0}^{M-1} x_p[m] \exp\!\big\{% -2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

   Обратите внимание, что линейная фаза \(\phi_m\) (см. phase_shift) может быть указан, что соответствует сдвигу ввода на \(\phi_m\) образцы. По умолчанию \(\phi_m = \lfloor M/2\rfloor\) (соответствует по определению phase_shift = 0), который подавляет линейные фазовые компоненты для несдвинутых сигналов. Кроме того, БПФ может быть передискретизировано путем дополнения \(w[m]\) с нулями. Это может быть достигнуто указанием mfft должно быть больше длины окна m_num— это устанавливает \(M\) to mfft (подразумевая, что также \(w[m]:=0\) для \(m\not\in\{0, 1, \ldots, M-1\}\) выполняется).

Обратное коротковременное преобразование Фурье (istft) реализовано путем обращения этих двух шагов:

1. Выполнить обратное дискретное преобразование Фурье, т.е.

   \[x_p[m] = \frac{1}{M}\sum_{q=0}^M S[q, p]\, \exp\!\big\{ 2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

2. Суммирование сдвинутых срезов, взвешенных по \(w_d[m]\) для восстановления исходного сигнала, т.е.,

   \[x[k] = \sum_p x_p\!\big[\mu_p(k)\big]\, w_d\!\big[\mu_p(k)\big]\ ,\quad \mu_p(k) = k + \lfloor M/2\rfloor - h p\]

   для \(k \in [0, \ldots, n-1]\). \(w_d[m]\) является так называемым двойным окном \(w[m]\) и также состоит из \(M\) выборки.

Обратите внимание, что обратное STFT не обязательно существует для всех окон и размеров шага. Для заданного окна \(w[m]\) шаг перекрытия \(h\) должно быть достаточно малым, чтобы гарантировать, что каждая выборка \(x[k]\) затронут ненулевым значением хотя бы одного оконного среза. Это иногда называют "условием ненулевого перекрытия" (см. check_NOLA). Некоторые дополнительные детали приведены в подразделе Обратное STFT и двойные окна.

Скользящие окна

Этот подраздел обсуждает, как индексируется скользящее окно в ShortTimeFFT на примере: Рассмотрим окно длиной 6 с hop интервал двух и интервал выборки T единицы, например, ShortTimeFFT (np.ones(6), 2, fs=1). Следующее изображение схематично изображает первые четыре позиции окна, также называемые временными срезами:

Ось X обозначает время \(t\), что соответствует индексу выборки k обозначено нижним рядом синих прямоугольников. Ось Y обозначает индекс временного среза \(p\). Сигнал \(x[k]\) начинается с индекса \(k=0\) и отмечено светло-синим фоном. По определению нулевой срез (\(p=0\)) центрирован в \(t=0\). Центр каждого среза (m_num_mid), здесь в качестве образца 6//2=3, отмечен текстом "mid". По умолчанию stft вычисляет все срезы, которые частично перекрываются с сигналом. Следовательно, первый срез находится на p_min = -1 с наименьшим индексом выборки равным k_min = -5. Первый индекс выборки, на который не влияет срез, выходящий за левую границу сигнала, равен \(p_{lb} = 2\) и первый индекс выборки, не затронутый граничными эффектами, это \(k_{lb} = 5\). Свойство lower_border_end возвращает кортеж \((k_{lb}, p_{lb})\).

Поведение в конце сигнала показано для сигнала с \(n=50\) образцы ниже, как показано синим фоном:

Здесь последний срез имеет индекс \(p=26\). Следовательно, следуя Python соглашению о конечном индексе вне диапазона, p_max = 27 указывает на первый срез, не касающийся сигнала. Соответствующий индекс выборки: k_max = 55. Первый срез, который выступает вправо, это \(p_{ub} = 24\) с его первой выборкой в \(k_{ub}=45\). Функция upper_border_begin возвращает кортеж \((k_{ub}, p_{ub})\).

Обратное STFT и двойные окна

Термин двойное окно происходит из теории фреймов [10] где фрейм — это разложение в ряд, которое может представлять любую функцию в заданном гильбертовом пространстве. Там разложения \(\{g_k\}\) и \(\{h_k\}\) являются двойственными фреймами, если для всех функций \(f\) в заданном гильбертовом пространстве \(\mathcal{H}\)

\[f = \sum_{k\in\IN} \langle f, g_k\rangle h_k = \sum_{k\in\IN} \langle f, h_k\rangle g_k\ , \quad f \in \mathcal{H}\ ,\]

выполняется, где \(\langle ., .\rangle\) обозначает скалярное произведение \(\mathcal{H}\). Все кадры имеют двойные кадры [10].

STFT, оцененный только в дискретных точках сетки \(S(q \Delta f, p\Delta t)\) называется "рамкой Габора" в литературе [9] [10]. Поскольку носитель окна \(w[m]\) ограничен конечным интервалом, ShortTimeFFT относится к классу так называемых "безболезненных неортогональных разложений" [9]. В этом случае двойные окна всегда имеют одинаковую область определения и могут быть вычислены путем обращения диагональной матрицы. Грубый вывод, требующий лишь некоторого понимания манипулирования матрицами, будет кратко изложен далее:

Поскольку STFT, заданный в уравнении. : TST: исправить некорректные тесты signal.sosfilt является линейным отображением в \(x[k]\), это может быть выражено в векторно-матричной нотации. Это позволяет нам выразить обратное через формальное решение метода наименьших квадратов (как в lstsq), что приводит к красивому и простому результату.

Начнём с переформулировки оконной функции из уравнения. (9)

(11)\[\begin{split} \vb{x}_p = \vb{W}_{\!p}\,\vb{x} = \begin{bmatrix} \cdots & 0 & w[0] & 0 & \cdots&&&\\ & \cdots & 0 & w[1] & 0 & \cdots&&\\ & & & & \ddots&&&\\ &&\cdots & 0 & 0 & w[M-1] & 0 & \cdots \end{bmatrix}\begin{bmatrix} x[0]\\ x[1]\\ \vdots\\ x[N-1] \end{bmatrix} ,\end{split}\]

где \(M\times N\) матрица \(\vb{W}_{\!p}\) имеет только ненулевые элементы на \((ph)\)-я побочная диагональ, т.е.,

(12)\[\begin{split} W_p[m,k] = w[m]\, \delta_{m+ph,k}\ ,\quad \delta_{k,l} &= \begin{cases} 1 & \text{ for } k=l\ ,\\ 0 & \text{ elsewhere ,} \end{cases}\end{split}\]

с \(\delta_{k,l}\) является дельтой Кронекера. Уравнение. (10) может быть выражен как

(13)\[\vb{s}_p = \vb{F}\,\vb{x}_p \quad\text{with}\quad F[q,m] = \frac{1}{\sqrt{M}}\exp\!\big\{-2\jj\pi (q + \phi_m)\, m / M\big\}\ ,\]

что позволяет получить STFT для \(p\)-й срез для записи как

(14)\[\vb{s}_p = \vb{F}\vb{W}_{\!p}\,\vb{x} =: \vb{G}_p\,\vb{x} \quad\text{with}\quad s_p[q] = S[p,q]\ .\]

Из-за масштабного коэффициента \(M^{-1/2}\), \(\vb{F}\) является унитарной, т.е. обратная матрица равна её сопряжённой транспонированной, что означает \(\conjT{\vb{F}}\vb{F} = \vb{I}\). Другие масштабирования, например, как в уравнении (6), также допускаются, но в этом разделе они немного усложнят обозначения.

Чтобы получить единое векторно-матричное уравнение для STFT, срезы объединяются в один вектор, т.е.,

\[\begin{split}\vb{s} := \begin{bmatrix} \vb{s}_0\\ \vb{s}_1\\ \vdots\\ \vb{s}_{P-1} \end{bmatrix} = \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix}\, \vb{x} =: \vb{G}\, \vb{x}\ ,\end{split}\]

где \(P\) это количество столбцов результирующего STFT. Чтобы инвертировать это уравнение, используется псевдообратная матрица Мура-Пенроуза \(\vb{G}^\dagger\) может быть использован

(15)\[\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\, \conjT{\vb{G}} \vb{s} =: \vb{G}^\dagger \vb{s}\ ,\]

который существует, если

(16)\[\begin{split} \vb{D} := \conjT{\vb{G}}\vb{G} = \begin{bmatrix} \conjT{\vb{G}_0}& \conjT{\vb{G}_1}& \cdots & \conjT{\vb{G}_{P-1}} \end{bmatrix}^T \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p \ .\end{split}\]

обратима. Тогда \(\vb{x} = \vb{G}^\dagger\vb{G}\,\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\,\conjT{\vb{G}}\vb{G}\,\vb{x}\) очевидно выполняется. \(\vb{D}\) всегда является диагональной матрицей с неотрицательными диагональными элементами. Это становится ясно при упрощении \(\vb{D}\) далее к

(17)\[\vb{D} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p = \sum_{p=0}^{P-1} \conjT{(\vb{F}\,\vb{W}_{\!p})}\, \vb{F}\,\vb{W}_{\!p} = \sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\vb{W}_{\!p} =: \sum_{p=0}^{P-1} \vb{D}_p\]

из-за \(\vb{F}\) является унитарной. Более того

(18)\[\begin{split}D_p[r,s] &= \sum_{m=0}^{M-1} \conj{W_p^T[r,m]}\,W_p[m,s] = \sum_{m=0}^{M-1} \left(\conj{w[m]}\, \delta_{m+ph,r}\right) \left(w[m]\, \delta_{m+ph,s}\right)\\ &= \sum_{m=0}^{M-1} \big|w[m]\big|^2\, \delta_{r,s}\, \delta_{r,m+ph}\ .\end{split}\]

показывает, что \(\vb{D}_p\) является диагональной матрицей с неотрицательными элементами. Следовательно, суммирование \(\vb{D}_p\) сохраняет это свойство. Это позволяет упростить уравнение. (15) далее, т.е.,

(19)\[\begin{split}\vb{x} &= \vb{D}^{-1} \conjT{\vb{G}}\vb{s} = \sum_{p=0}^{P-1} \vb{D}^{-1}\conjT{\vb{W}_{\!p}}\, \conjT{\vb{F}}\vb{s}_p = \sum_{p=0}^{P-1} (\conj{\vb{W}_{\!p}\vb{D}^{-1}})^T\, \conjT{\vb{F}}\vb{s}_p\\ &=: \sum_{p=0}^{P-1}\conjT{\vb{U}_p}\,\conjT{\vb{F}}\vb{s}_p\ .\end{split}\]

Используя уравнение. (12), (17), (18), \(\vb{U}_p=\vb{W}_{\!p}\vb{D}^{-1}\) может быть выражено как

(20)\[\begin{split}U_p[m, k] &= W[m,k]\, D^{-1}[k,k] = \left(w[m] \delta_{m+ph,k}\right) \inv{\sum_{\eta=0}^{P-1} \vb{D}_\eta[k,k]} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1}\sum_{\mu=0}^{M-1} \big|w[\mu]\big|^2\,\delta_{m+ph, \mu+\eta h}} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1} \big|w[m+(p-\eta)h]\big|^2} \delta_{m+ph,k} \ .\end{split}\]

Это показывает \(\vb{U}_p\) имеет идентичную структуру с \(\vb{W}_p\) в уравнении. (12), т.е. имеющий только ненулевые элементы на \((ph)\)-я побочная диагональ. Сумма в обратной матрице может быть интерпретирована как скользящая \(|w[\mu]|^2\) над \(w[m]\) (с включённой инверсией), поэтому только компоненты, перекрывающиеся с \(w[m]\) имеют эффект. Следовательно, все \(U_p[m, k]\) достаточно далеко от границы являются идентичными окнами. Чтобы обойти граничные эффекты, \(x[k]\) дополняется нулями, увеличивая \(\vb{U}\) так что все срезы, которые касаются \(x[k]\) содержат идентичное двойное окно

(21)\[\begin{split} w_d[m] &= w[m] \inv{\sum_{\eta\in\IZ} \big|w[m + \eta\, h]\big|^2}\\ &=\ w[m] \inv{\sum_{l=0}^{M-1} \big|w[l]\big|^2 \delta_{l+m,\eta h}}\ , \quad \eta\in \IZ\ .\end{split}\]

Поскольку \(w[m] = 0\) выполняется для \(m \not\in\{0, \ldots, M-1\}\), требуется суммировать только по индексам \(\eta\) выполнение \(|\eta| < M/h\). Второе выражение — альтернативная форма путём суммирования от индекса \(l=0\) to \(M\) с шагом индекса \(h\). \(\delta_{l+m,\eta h}\) является обозначением дельты Кронекера для (l+m) % h == 0. Название двойного окна может быть обосновано вставкой уравнения. (14) в Ур. (19), т.е.,

(22)\[ \vb{x} = \sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\conjT{\vb{F}}\, \vb{F}\,\vb{W}_{\!p}\,\vb{x} = \left(\sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\vb{W}_{\!p}\right)\vb{x}\ ,\]

показывая, что \(\vb{U}_p\) и \(\vb{W}_{\!p}\) взаимозаменяемы. Из-за \(\vb{U}_p\) и \(\vb{W}_{\!p}\) имеющую ту же структуру, что дана в уравнении. (11), Ур. (22) содержит общее условие для всех возможных двойных окон, т.е.,

(23)\[\sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\,\vb{U}_p = \vb{I} \quad\Leftrightarrow\quad \sum_{p=0}^{P-1} \sum_{m=0}^{M-1} \conj{w[m]} u[m]\, \delta_{m+ph,i}\, \delta_{m+ph,j} = \delta_{i,j}\]

который может быть преобразован в

(24)\[\conjT{\vb{V}}\,\vb{u} = \vb{1}\ , \qquad V[i,j] := w[i]\, \delta_{i, j+ph}\ , \qquad \vb{V}\in \IC^{M\times h},\ p\in\IZ\ ,\]

где \(\vb{1}\in\IR^h\) является вектором единиц. Причина, по которой \(\vb{V}\) имеет только \(h\) столбцы в том, что \(i\)-й и \((i+m)\)-я строка, \(i\in\IN\), в уравнении. (22) идентичны. Следовательно, есть только \(h\) различные уравнения.

Практический интерес представляет нахождение допустимого двойного окна \(\vb{u}_d\) ближайший к заданному вектору \(\vb{d}\in\IC^M\). Используя \(h\)-мерный вектор \(\vb{\lambda}\) множителей Лагранжа, получаем выпуклую квадратичную задачу программирования

\[\begin{split}\vb{u}_d = \min_{\vb{u}}{ \frac{1}{2}\lVert\vb{d} - \vb{u}\rVert^2 } \quad\text{w.r.t.}\quad \conjT{\vb{V}}\vb{u} = \vb{1} \qquad\Leftrightarrow\qquad \begin{bmatrix} \vb{I} & \vb{V}\\ \conjT{\vb{V}} & \vb{0} \end{bmatrix} \begin{bmatrix} \vb{u}_d \\ \vb{\lambda} \end{bmatrix} = \begin{bmatrix} \vb{d}\\ \vb{1} \end{bmatrix}\ .\end{split}\]

Замкнутое решение может быть вычислено путём обращения \(2\times2\) блочная матрица символически, что дает

(25)\[\begin{split}\vb{u}_d &= \underbrace{\vb{V}\inv{\conjT{\vb{V}}\vb{V}}}_{% =:\vb{Q}\in\IC^{M\times h}} \vb{1} + \big(\vb{I} - \vb{Q}\conjT{\vb{V}}\big)\vb{d} = \vb{w}_d + \vb{d} - \vb{q}_d\ ,\\ \vb{w}_d &= \vb{Q}\vb{1}\ ,\qquad \vb{q}_d = \vb{Q}\conjT{\vb{V}}\vb{d}\ ,\\ Q[i,j] &= \frac{ w[i] \delta_{i-j, \eta h} }{% \sum_{k=0}^M |w[k]|^2\,\delta_{i-k, \xi h} } ,\qquad w_d[i] = \frac{w[i] }{ \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \xi h} }\ ,\\ q_d[i] &= w[i] \frac{\sum_{j=1}^h \delta_{i-j, \eta h} \sum_{l=1}^M \conj{w[l]} d[l] \delta_{j-l, \xi h} }{% \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \zeta h} } = w_d[i] \sum_{l=1}^M \conj{w[l]} d[l] \delta_{i-l, \eta h}\ ,\end{split}\]

с \(\eta,\xi,\zeta\in\IZ\). Обратите внимание, что первый член \(\vb{w}_d\) равно решению, приведенному в уравнении. (21) и что обратная матрица \(\conjT{\vb{V}}\vb{V}\) должен существовать, иначе STFT необратим. Когда \(\vb{d}=\vb{0}\), решение \(\vb{w}_d\) получено. Следовательно, \(\vb{w}_d\) минимизирует \(L^2\)-norm \(\lVert\vb{u}\rVert\), что является обоснованием для его названия «каноническое двойственное окно». Иногда более желательно найти ближайший вектор с учётом направления и игнорируя длину вектора. Это может быть достигнуто путём введения масштабного коэффициента \(\alpha\in\IC\) для минимизации \(\lVert\alpha\vb{d} - \vb{u}\rVert^2\). Поскольку уравнение. (25) уже предоставляет общее решение, мы можем написать

\[\begin{split} \alpha_{\min} &= \min_{\alpha}{ \frac{1}{2}\big\lVert\alpha\vb{d} - \vb{u}_d(\alpha)\big\rVert^2 }\ ,\qquad \vb{u}_d(\alpha) = \vb{w}_d + \alpha\vb{d} - \alpha\vb{q}_d \qquad\Leftrightarrow\\ \alpha_{\min} &= \conjT{\vb{q}_d}\vb{w}_d \big/\, \conjT{\vb{q}_d}\vb{q}_d \ .\end{split}\]

Jerry Li + \(w[m]\) и двойное окно \(u[m]\) равны, могут быть легко выведены из уравнения. (23) в результате \(h\) условия вида

(26)\[\sum_{p=0}^{\lfloor M / h \rfloor} \big|w[m+ph]\big|^2 = 1\ , \qquad m \in \{0, \ldots, h-1\}\ .\]

Обратите внимание, что каждый образец окна \(w[m]\) появляется только один раз в \(h\) уравнений. Чтобы найти ближайшее окно \(\vb{w}\) для заданного окна \(\vb{d}\) просто: Разделить \(\vb{d}\) согласно уравнению. (26) и нормализовать длину каждого раздела до единицы. В этом случае \(w[m]\) также является каноническим двойным окном, что можно увидеть, распознав, что установка \(u[m]=w[m]\) в уравнении. (24) эквивалентно знаменателю в уравнении. (21) равным единице.

Кроме того, если Ур. (26) выполняется, матрица \(\vb{D}\) уравнения (16) является единичной матрицей, делая STFT \(\vb{G}\) унитарное отображение, т.е., \(\conjT{\vb{G}}\vb{G}=\vb{I}\). Обратите внимание, что это справедливо только для унитарного ДПФ из уравнения (13) используется. The ShortTimeFFT реализация использует стандартное ДПФ из уравнения. (6). Следовательно, скалярное произведение в пространстве STFT должно быть масштабировано на \(1/M\) чтобы гарантировать ключевое свойство унитарных отображений — равенство скалярных произведений. Т.е.,

(27)\[\langle x, y\rangle = \sum_k x[k]\, \conj{y[k]} \stackrel{\stackrel{\text{unitary}}{\downarrow}}{=} \frac{1}{M}\sum_{q,p} S_x[q,p]\, \conj{S_y[q,p]}\ ,\]

с \(S_{x,y}\) является STFT для \(x,y\). Альтернативно, окно может быть масштабировано с помощью \(1/\sqrt{M}\) и двойственная через \(\sqrt{M}\) для получения унитарного отображения, которое реализовано в from_win_equals_dual.

Сравнение с устаревшей реализацией

Функции stft, istftдолжны быть включены в старые категории. Значения, которые были в удаленных категориях, будут установлены в NaN spectrogram предшествуют ShortTimeFFT реализация. Этот раздел обсуждает ключевые различия между старой "устаревшей" и новой ShortTimeFFT реализации. Основная мотивация для переписывания заключалась в понимании, что интегрирование двойные окна не могло быть выполнено разумным образом без нарушения совместимости. Это открыло возможность переосмыслить структуру кода и параметризацию, сделав некоторые неявные поведения более явными.

Следующий пример сравнивает два STFT комплексного чирп-сигнала с отрицательным наклоном:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import fftshift
>>> from scipy.signal import stft, istft, spectrogram, ShortTimeFFT
...
>>> fs, N = 200, 1001  # 200 Hz sampling rate for 5 s signal
>>> t_z = np.arange(N) / fs  # time indexes for signal
>>> z = np.exp(2j*np.pi*70 * (t_z - 0.2*t_z**2))  # complex-valued chirp
...
>>> nperseg, noverlap = 50, 40
>>> win = ('gaussian', 1e-2 * fs)  # Gaussian with 0.01 s standard dev.
...
>>> # Legacy STFT:
>>> f0_u, t0, Sz0_u = stft(z, fs, win, nperseg, noverlap,
...                        return_onesided=False, scaling='spectrum')
>>> f0, Sz0 = fftshift(f0_u), fftshift(Sz0_u, axes=0)
...
>>> # New STFT:
>>> SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap, fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz1 = SFT.stft(z)
...
>>> # Plot results:
>>> fig1, axx = plt.subplots(2, 1, sharex='all', sharey='all',
...                          figsize=(6., 5.))  # enlarge figure a bit
>>> t_lo, t_hi, f_lo, f_hi = SFT.extent(N, center_bins=True)
>>> axx[0].set_title(r"Legacy stft() produces $%d\times%d$ points" % Sz0.T.shape)
>>> axx[0].set_xlim(t_lo, t_hi)
>>> axx[0].set_ylim(f_lo, f_hi)
>>> axx[1].set_title(r"ShortTimeFFT produces $%d\times%d$ points" % Sz1.T.shape)
>>> axx[1].set_xlabel(rf"Time $t$ in seconds ($\Delta t= {SFT.delta_t:g}\,$s)")
...
>>> # Calculate extent of plot with centered bins since
>>> # imshow does not interpolate by default:
>>> dt2 = (nperseg-noverlap) / fs / 2  # equals SFT.delta_t / 2
>>> df2 = fs / nperseg / 2  # equals SFT.delta_f / 2
>>> extent0 = (-dt2, t0[-1] + dt2, f0[0] - df2, f0[-1] - df2)
>>> extent1 = SFT.extent(N, center_bins=True)
...
>>> kw = dict(origin='lower', aspect='auto', cmap='viridis')
>>> im1a = axx[0].imshow(abs(Sz0), extent=extent0, **kw)
>>> im1b = axx[1].imshow(abs(Sz1), extent=extent1, **kw)
>>> fig1.colorbar(im1b, ax=axx, label="Magnitude $|S_z(t, f)|$")
>>> _ = fig1.supylabel(r"Frequency $f$ in Hertz ($\Delta f = %g\,$Hz)" %
...                    SFT.delta_f, x=0.08, y=0.5, fontsize='medium')
>>> plt.show()

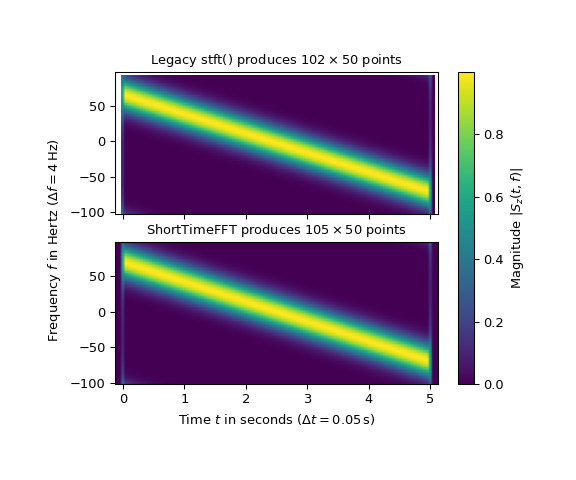
То, что ShortTimeFFT создает на 3 временных среза больше, чем устаревшая версия, что является основным отличием. Как указано в Скользящие окна раздел, все срезы, которые касаются сигнала, включаются в новую версию. Это имеет преимущество, что STFT может быть нарезан и собран заново, как показано в ShortTimeFFT пример кода. Кроме того, использование всех касающихся срезов делает ISTFT более устойчивым в случае окон, которые где-то равны нулю.

Обратите внимание, что срезы с одинаковыми временными метками дают одинаковые результаты (с точностью до численной погрешности), т.е.:

>>> np.allclose(Sz0, Sz1[:, 2:-1])
True

Обычно эти дополнительные срезы содержат ненулевые значения. Из-за большого перекрытия в нашем примере они довольно малы. Например:

>>> abs(Sz1[:, 1]).min(), abs(Sz1[:, 1]).max()
(6.925060911593139e-07, 8.00271269218721e-07)

ISTFT может быть использовано для восстановления исходного сигнала:

>>> t0_r, z0_r = istft(Sz0_u, fs, win, nperseg, noverlap,
...                    input_onesided=False, scaling='spectrum')
>>> z1_r = SFT.istft(Sz1, k1=N)
...
>>> len(z0_r), len(z)
(1010, 1001)
>>> np.allclose(z0_r[:N], z)
True
>>> np.allclose(z1_r, z)
True

Обратите внимание, что устаревшая реализация возвращает сигнал, который длиннее исходного. С другой стороны, новая istft позволяет явно указать начальный индекс k0 и конечный индекс k1 восстановленного сигнала. Расхождение в длине в старой реализации вызвано тем, что длина сигнала не кратна количеству сегментов.

Дополнительные различия между новой и устаревшей версиями в этом примере:

• Параметр fft_mode='centered' гарантирует, что нулевая частота вертикально центрирована для двусторонних БПФ на графике. При использовании устаревшей реализации, fftshift должен быть использован. fft_mode='twosided' производит такое же поведение, как и старая версия.

• Параметр phase_shift=None обеспечивает идентичные фазы двух версий. ShortTimeFFTзначение по умолчанию 0 производит срезы STFT с дополнительным линейным фазовым членом.

Спектрограмма определяется как квадрат модуля STFT [9]. spectrogram предоставленный ShortTimeFFT придерживается этого определения, т.е.:

>>> np.allclose(SFT.spectrogram(z), abs(Sz1)**2)
True

С другой стороны, устаревший spectrogram предоставляет другую реализацию STFT с ключевым отличием в обработке границ сигнала. Следующий пример показывает, как использовать ShortTimeFFT для получения идентичного SFT, как при использовании устаревшего spectrogram:

>>> # Legacy spectrogram (detrending for complex signals not useful):
>>> f2_u, t2, Sz2_u = spectrogram(z, fs, win, nperseg, noverlap,
...                               detrend=None, return_onesided=False,
...                               scaling='spectrum', mode='complex')
>>> f2, Sz2 = fftshift(f2_u), fftshift(Sz2_u, axes=0)
...
>>> # New STFT:
... SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap,
...                                fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz3 = SFT.stft(z, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
>>> t3 = SFT.t(N, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
...
>>> np.allclose(t2, t3)
True
>>> np.allclose(f2, SFT.f)
True
>>> np.allclose(Sz2, Sz3)
True

Отличие от других STFT в том, что временные срезы начинаются не с 0, а с nperseg//2, т.е.:

>>> t2
array([0.125, 0.175, 0.225, 0.275, 0.325, 0.375, 0.425, 0.475, 0.525,
       ...
       4.625, 4.675, 4.725, 4.775, 4.825, 4.875])

Биномиальное распределение stft параметризация.

Используя mode параметр, устаревший spectrogram также может возвращать 'angle', 'phase', 'psd' или 'magnitude'. Параметр scaling поведение устаревшего spectrogram не является простой, поскольку зависит от параметров mode, scaling и return_onesided. Не существует прямого соответствия для всех комбинаций в ShortTimeFFT, поскольку он предоставляет только 'величину', 'psd' или ничего scaling окна вообще. Следующая таблица показывает эти соответствия:

Наследие spectrogram				ShortTimeFFT
mode	масштабирование	return_onesided		fft_mode	scaling
psd	плотность	True		onesided2X	psd
psd	плотность	False		двусторонний	psd
величина	спектр	True		односторонний	величина
величина	спектр	False		двусторонний	величина
комплексный	спектр	True		односторонний	величина
комплексный	спектр	False		двусторонний	величина
psd	спектр	True		—	—
psd	спектр	False		—	—
комплексный	плотность	True		—	—
комплексный	плотность	False		—	—
величина	плотность	True		—	—
величина	плотность	False		—	—
—	—	—		*	None

При использовании onesided вывод на комплексных входных сигналах, старый spectrogram переключается на two-sided режим. The ShortTimeFFT вызывает TypeError, поскольку используемый rfft функция принимает только действительные входные значения. Обратитесь к Спектральный анализ раздел выше для обсуждения различных спектральных представлений, которые индуцируются различными параметризациями.

Ссылки

Дополнительная литература и связанное программное обеспечение:

[1]

«Преобразование Фурье», Википедия, https://en.wikipedia.org/wiki/Fourier_transform

[2]

“Спектральная плотность”, Википедия, https://en.wikipedia.org/wiki/Spectral_density

[3]

“Дискретное преобразование Фурье”, Википедия, https://en.wikipedia.org/wiki/Discrete_Fourier_transform

[4]

“Спектральная утечка”, Википедия, https://en.wikipedia.org/wiki/Spectral_leakage

[5]

“Теорема отсчётов Найквиста–Шеннона”, Википедия, https://en.wikipedia.org/wiki/Теорема_дискретизации_Найквиста-Шеннона

[6]

N.R. Lomb «Least-squares frequency analysis of unequally spaced data», Astrophysics and Space Science, vol 39, pp. 447-462, 1976

[7]

J.D. Scargle «Исследования в анализе астрономических временных рядов. II - Статистические аспекты спектрального анализа неравномерно распределенных данных», The Astrophysical Journal, том 263, стр. 835-853, 1982

[8]

M. Zechmeister и M. Kürster, “Обобщённый периодограммный метод Ломба-Скаргла. Новая формализация для плавающего среднего и кеплеровских периодограмм,” Astronomy and Astrophysics, vol. 496, pp. 577-584, 2009

[9] (1,2,3,4)

Карлхайнц Грёхениг: "Основы анализа время-частота", Birkhäuser Boston 2001, DOI:10.1007/978-1-4612-0003-1

[10] (1,2,3)

Ole Christensen: "An Introduction to Frames and Riesz Bases", Birkhäuser Boston 2016, DOI:10.1007/978-3-319-25613-9