scipy.signal.

ZoomFFT

класс scipy.signal.ZoomFFT(n, fn, m=None, *, fs=2, конечная точка=False)

Создать вызываемую функцию преобразования зумированного БПФ.

Это специализация z-преобразования чирпа (CZT) для набора равноотстоящих частот вокруг единичной окружности, используемых для вычисления секции БПФ более эффективно, чем вычисление всего БПФ и усечение.

Параметры:

nint

Размер сигнала.

fnarray_like

Последовательность длины 2 [f1, f2] задающий диапазон частот, или скаляр, для которого диапазон [0, fn] предполагается.

mint, необязательный

Количество точек для вычисления. По умолчанию n.

fsfloat, опционально

Частота дискретизации. Если fs=10 представляла 10 кГц, например, тогда f1 и f2 также будет задана в кГц. Частота дискретизации по умолчанию равна 2, поэтому f1 и f2 должен быть в диапазоне [0, 1], чтобы сохранить преобразование ниже частоты Найквиста.

конечная точкаbool, необязательно

Если True, f2 Jacques Gaudin +

Методы

__call__(x, *[, axis])	Вычислить чирп Z-преобразование сигнала.
points()	Вернуть точки, в которых вычисляется z-преобразование чирпа.

Возвращает:

fZoomFFT

Вызываемый объект f(x, axis=-1) для вычисления зум-БПФ на x.

Смотрите также

zoom_fft

Удобная функция для вычисления зум-БПФ.

Примечания

Значения по умолчанию выбраны так, чтобы f(x, 2) эквивалентно fft.fft(x) и, если m > len(x), что f(x, 2, m) эквивалентно fft.fft(x, m).

Частота дискретизации равна 1/dt, временной шаг между выборками в сигнале x. Единичная окружность соответствует частотам от 0 до частоты дискретизации. Частота дискретизации по умолчанию 2 означает, что f1, f2 значения до частоты Найквиста находятся в диапазоне [0, 1). Для f1, f2 значения, выраженные в радианах, следует использовать частоту дискретизации 2*pi.

Помните, что увеличенное БПФ может только интерполировать точки существующего БПФ. Оно не может помочь разрешить две отдельные близкие частоты. Разрешение по частоте можно увеличить только увеличением времени захвата.

Эти функции реализованы с использованием алгоритма Блюстейна (как и scipy.fft). [2]

Ссылки

[1]

Steve Alan Shilling, “A study of the chirp z-transform and its applications”, стр. 29 (1970) теперь выдают информативную ошибку на пустой ввод вместо достижения предела рекурсии.

[2]

Leo I. Bluestein, «A linear filtering approach to the computation of the discrete Fourier transform,» Northeast Electronics Research and Engineering Meeting Record 10, 218-219 (1968).

Примеры

Попробуйте в вашем браузере!

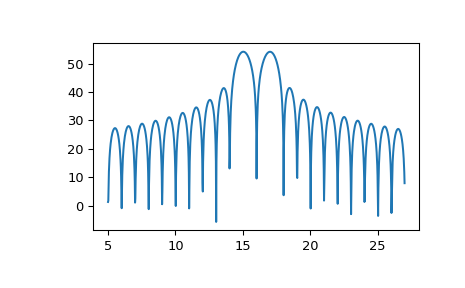
Для построения графика результатов преобразования используйте что-то вроде следующего:

>>> import numpy as np
>>> from scipy.signal import ZoomFFT
>>> t = np.linspace(0, 1, 1021)
>>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t)
>>> f1, f2 = 5, 27
>>> transform = ZoomFFT(len(x), [f1, f2], len(x), fs=1021)
>>> X = transform(x)
>>> f = np.linspace(f1, f2, len(x))
>>> import matplotlib.pyplot as plt
>>> plt.plot(f, 20*np.log10(np.abs(X)))
>>> plt.show()

НазадОткрыть во вкладке