scipy.signal.

cheb1ord#

scipy.signal.cheb1ord(wp, ws, gpass, gstop, аналог=False, fs=None)[источник]#

Выбор порядка фильтра Чебышёва типа I.

Вернуть порядок цифрового или аналогового фильтра Чебышёва типа I наименьшего порядка, который теряет не более чем gpass дБ в полосе пропускания и имеет как минимум gstop Затухание в дБ в полосе задерживания.

Параметры:

wp, wsfloat

Частоты границ полосы пропускания и задерживания.

Для цифровых фильтров они имеют те же единицы измерения, что и fs. По умолчанию, fs составляет 2 полуцикла/сэмпл, поэтому они нормализованы от 0 до 1, где 1 — частота Найквиста. (wp и ws соответственно, в полупериодах / отсчёт.) Например:

ФНЧ: wp = 0.2, ws = 0.3

Высокочастотный фильтр: wp = 0.3, ws = 0.2

Полосовой фильтр: wp = [0.2, 0.5], ws = [0.1, 0.6]

Полосовой заградительный: wp = [0.1, 0.6], ws = [0.2, 0.5]

Для аналоговых фильтров, wp и ws являются угловыми частотами (например, рад/с).

gpassfloat

Максимальные потери в полосе пропускания (дБ).

gstopfloat

Минимальное затухание в полосе задерживания (дБ).

аналогbool, необязательно

Если True, возвращает аналоговый фильтр, в противном случае возвращается цифровой фильтр.

fsfloat, опционально

Частота дискретизации цифровой системы.

Добавлено в версии 1.2.0.

Возвращает:

ordint: Минимальный порядок для фильтра Чебышева типа I, удовлетворяющего спецификациям.
wnndarray или float: Натуральная частота Чебышёва (частота «3 дБ») для использования с cheby1 для получения результатов фильтрации. Если fs указан, это в тех же единицах, и fs также должен быть передан в cheby1.

Смотрите также

cheby1: Проектирование фильтра с использованием порядка и критических точек
buttord: Найти порядок и критические точки по спецификациям полосы пропускания и полосы задерживания
cheb2ord, ellipord
iirfilter: Общее проектирование фильтров с использованием порядка и критических частот
iirdesign: Общее проектирование фильтра с использованием спецификаций полосы пропускания и задерживания

Примеры

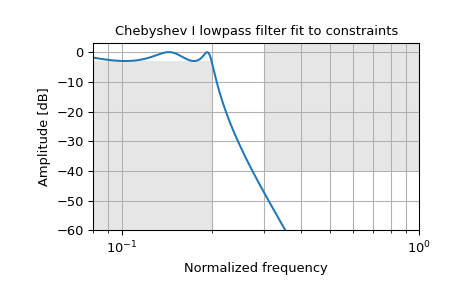
Спроектировать цифровой фильтр нижних частот так, чтобы полоса пропускания была в пределах 3 дБ до 0.2*(fs/2), при этом ослабляя не менее -40 дБ выше 0.3*(fs/2). Построить его амплитудно-частотную характеристику, показывая ограничения полосы пропускания и задерживания серым цветом.

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> N, Wn = signal.cheb1ord(0.2, 0.3, 3, 40)
>>> b, a = signal.cheby1(N, 3, Wn, 'low')
>>> w, h = signal.freqz(b, a)
>>> plt.semilogx(w / np.pi, 20 * np.log10(abs(h)))
>>> plt.title('Chebyshev I lowpass filter fit to constraints')
>>> plt.xlabel('Normalized frequency')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(which='both', axis='both')
>>> plt.fill([.01, 0.2, 0.2, .01], [-3, -3, -99, -99], '0.9', lw=0) # stop
>>> plt.fill([0.3, 0.3,   2,   2], [ 9, -40, -40,  9], '0.9', lw=0) # pass
>>> plt.axis([0.08, 1, -60, 3])
>>> plt.show()

../../_images/scipy-signal-cheb1ord-1.png