scipy.signal.

iirdesign#

scipy.signal.iirdesign(wp, ws, gpass, gstop, аналог=False, ftype='ellip', вывод='ba', fs=None)[источник]#

Полное проектирование цифровых и аналоговых фильтров IIR.

При заданных частотах полосы пропускания и задерживания, а также коэффициентах усиления, построить аналоговый или цифровой КИХ-фильтр минимального порядка для заданного базового типа. Возвращает результат в форме числителя и знаменателя ('ba'), полюсов и нулей ('zpk') или звеньев второго порядка ('sos').

Параметры:

wp, wsfloat или array like, shape (2,)

Частоты среза полосы пропускания и полосы задерживания. Возможные значения: скаляры (для фильтров нижних и верхних частот) или диапазоны (для полосовых и режекторных фильтров). Для цифровых фильтров они выражены в тех же единицах, что и fs. По умолчанию, fs равно 2 полуцикла/сэмпл, поэтому они нормализованы от 0 до 1, где 1 — частота Найквиста. Например:

ФНЧ: wp = 0.2, ws = 0.3

Высокочастотный фильтр: wp = 0.3, ws = 0.2

Полосовой фильтр: wp = [0.2, 0.5], ws = [0.1, 0.6]

Полосовой заградительный: wp = [0.1, 0.6], ws = [0.2, 0.5]

Для аналоговых фильтров, wp и ws являются угловыми частотами (например, рад/с). Обратите внимание, что для полосовых и режекторных фильтров полоса пропускания должна строго лежать внутри полосы задерживания или наоборот. Также обратите внимание, что срез на краях полосы для IIR-фильтров определяется как половинная мощность, то есть -3 дБ, а не половинная амплитуда (-6 дБ), как для scipy.signal.fiwin.

gpassfloat

Максимальные потери в полосе пропускания (дБ).

gstopfloat

Минимальное затухание в полосе задерживания (дБ).

аналогbool, необязательно

Если True, возвращает аналоговый фильтр, в противном случае возвращается цифровой фильтр.

ftypestr, optional

Тип проектируемого IIR-фильтра:

Баттерворта : 'butter'

Чебышева I : 'cheby1'

Чебышёв II : ‘cheby2’

Кауэр/эллиптический: 'ellip'

вывод{‘ba’, ‘zpk’, ‘sos’}, опционально

Форма фильтра на выходе:

секции второго порядка (рекомендуется): ‘sos’

числитель/знаменатель (по умолчанию) : ‘ba’

полюс-ноль : ‘zpk’

В общем случае рекомендуется форма секций второго порядка (‘sos’), поскольку вывод коэффициентов для формы числителя/знаменателя (‘ba’) страдает от числовой неустойчивости. По причинам обратной совместимости форма по умолчанию — это форма числителя/знаменателя (‘ba’), где ‘b’ и ‘a’ в ‘ba’ относятся к общепринятым названиям используемых коэффициентов.

Примечание: использование формы секций второго порядка ('sos') иногда связано с дополнительными вычислительными затратами: для случаев интенсивного использования данных рекомендуется также исследовать форму числителя/знаменателя ('ba').

fsfloat, опционально

Частота дискретизации цифровой системы.

Добавлено в версии 1.2.0.

Возвращает:

b, aСоздать LinearOperators: Числитель (b) и знаменатель (a) полиномы IIR-фильтра. Возвращается только если output='ba'.
z, p, kndarray, ndarray, float: Нули, полюсы и коэффициент усиления системы передаточной функции фильтра IIR. Возвращается только если output='zpk'.
sosndarray: Представление фильтра IIR в виде звеньев второго порядка. Возвращается только если output='sos'.

Смотрите также

butter: Проектирование фильтра с использованием порядка и критических точек
cheby1, cheby2, ellip, bessel
buttord: Найти порядок и критические точки по спецификациям полосы пропускания и полосы задерживания
cheb1ord, cheb2ord, ellipord
iirfilter: Общее проектирование фильтров с использованием порядка и критических частот

Примечания

The 'sos' выходной параметр был добавлен в версии 0.16.0.

Примеры

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import matplotlib.ticker

>>> wp = 0.2
>>> ws = 0.3
>>> gpass = 1
>>> gstop = 40

>>> system = signal.iirdesign(wp, ws, gpass, gstop)
>>> w, h = signal.freqz(*system)

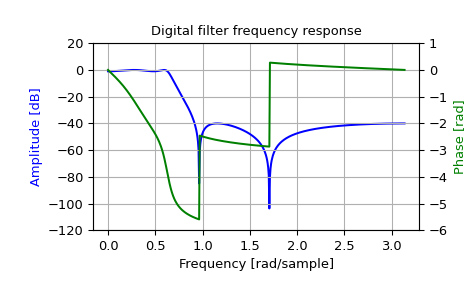
>>> fig, ax1 = plt.subplots()
>>> ax1.set_title('Digital filter frequency response')
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [rad/sample]')
>>> ax1.grid(True)
>>> ax1.set_ylim([-120, 20])
>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'g')
>>> ax2.set_ylabel('Phase [rad]', color='g')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> ax2.set_ylim([-6, 1])
>>> nticks = 8
>>> ax1.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))
>>> ax2.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))

../../_images/scipy-signal-iirdesign-1.png