scipy.signal.

dstep#

scipy.signal.dstep(система, x0=None, t=None, n=None)[источник]#

Ступенчатая реакция дискретной системы.

Параметры:

системаdlti | кортеж

Экземпляр класса LTI dlti или кортеж, описывающий систему. Количество элементов в кортеже определяет интерпретацию. Т.е.:

system: Экземпляр класса LTI dlti. Обратите внимание, что производные экземпляры, такие как экземпляры TransferFunction, ZerosPolesGain, или StateSpace, также допускаются.
(num, den, dt): Рациональный полином, как описано в TransferFunction. Коэффициенты полиномов должны быть указаны в порядке убывания степеней, например, z² + 3z + 5 должно быть представлено как [1, 3, 5].
(zeros, poles, gain, dt): Форма нулей, полюсов и коэффициента усиления, как описано в ZerosPolesGain.
(A, B, C, D, dt): Форма пространства состояний, как описано в StateSpace.

x0array_like, необязательный

Начальный вектор состояния. По умолчанию ноль.

tarray_like, необязательный

Временные точки. Вычисляются, если не заданы.

nint, необязательный

Количество временных точек для вычисления (если t не указан).

Возвращает:

toutndarray: Выходные временные точки, как одномерный массив.
youtкортеж ndarray: Переходная характеристика системы. Каждый элемент кортежа представляет выход системы на основе переходной характеристики на каждый вход.

Смотрите также

step, dimpulse, dlsim, cont2discrete

Примеры

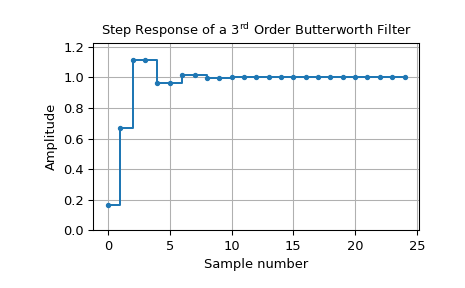
Следующий пример иллюстрирует, как создать цифровой фильтр Баттерворта и построить его переходную характеристику:

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
...
>>> dt = 1  # sampling interval is one => time unit is sample number
>>> bb, aa = signal.butter(3, 0.25, fs=1/dt)
>>> t, y = signal.dstep((bb, aa, dt), n=25)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.step(t, np.squeeze(y), '.-', where='post')
>>> ax0.set_title(r"Step Response of a $3^\text{rd}$ Order Butterworth Filter")
>>> ax0.set(xlabel='Sample number', ylabel='Amplitude', ylim=(0, 1.1*np.max(y)))
>>> ax0.grid()
>>> plt.show()