scipy.signal.

firls#

scipy.signal.firls(numtaps, bands, желаемый, *, вес=None, fs=None)[источник]#

Проектирование КИХ-фильтров с использованием минимизации среднеквадратичной ошибки.

Вычислить коэффициенты фильтра для линейно-фазового конечного импульсного отклика (FIR), который наилучшим образом аппроксимирует желаемую частотную характеристику, описанную bands и желаемый в смысле наименьших квадратов (т.е. интеграл взвешенной среднеквадратичной ошибки в указанных полосах минимизируется).

Параметры:

numtapsint: Количество отводов в КИХ-фильтре. numtaps должно быть нечётным.
bandsarray_like: Монотонная неубывающая последовательность, содержащая края полосы в Гц. Все элементы должны быть неотрицательными и не превышать частоту Найквиста, заданную nyq. Полосы задаются как частотные пары, поэтому, если используется одномерный массив, его длина должна быть четной, например, np.array([0, 1, 2, 3, 4, 5]). В качестве альтернативы полосы могут быть указаны как двумерный массив размером nx2, где n — количество полос, например, np.array([[0, 1], [2, 3], [4, 5]]).
желаемыйarray_like: Последовательность того же размера, что и bands содержащий желаемое усиление в начальной и конечной точках каждой полосы.
весarray_like, необязательный: Относительный вес, присваиваемый каждой полосе при решении задачи наименьших квадратов. вес должен быть вдвое меньше размера bands.
fsfloat, опционально: Частота дискретизации сигнала. Каждая частота в bands должно быть между 0 и fs/2 (включительно). По умолчанию 2.

Возвращает:

coeffsndarray: Коэффициенты оптимального (в смысле наименьших квадратов) КИХ-фильтра.

Смотрите также

firwin
firwin2
minimum_phase
remez

Примечания

Эта реализация следует алгоритму, приведенному в [1]. Как отмечено там, метод наименьших квадратов имеет несколько преимуществ:

Оптимально в смысле наименьших квадратов.

Простой, неитеративный метод.

Общее решение может быть получено путем решения линейной системы уравнений.

Позволяет использовать весовую функцию, зависящую от частоты.

Эта функция создает КИХ-фильтр с линейной фазой типа I, который содержит нечетное количество coeffs удовлетворяющий для \(n < numtaps\):

\[coeffs(n) = coeffs(numtaps - 1 - n)\]

Нечетное количество коэффициентов и симметрия фильтра избегают граничных условий, которые в противном случае могли бы возникнуть на частотах Найквиста и 0 (например, для вариантов Типа II, III или IV).

Добавлено в версии 0.18.

Ссылки

[1]

Иван Селезник, Проектирование КИХ-фильтров с линейной фазой методом наименьших квадратов. OpenStax CNX. 9 авг. 2005. https://eeweb.engineering.nyu.edu/iselesni/EL713/firls/firls.pdf

Примеры

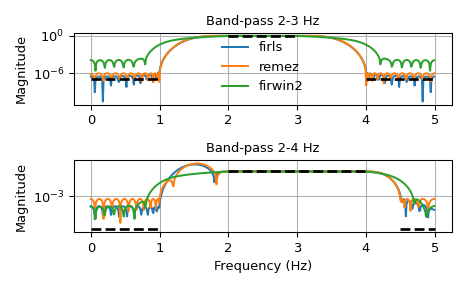
Мы хотим построить полосовой фильтр. Обратите внимание, что поведение в частотных диапазонах между нашими полосами задерживания и пропускания не определено и может давать выбросы в зависимости от параметров фильтра:

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> fig, axs = plt.subplots(2)
>>> fs = 10.0  # Hz
>>> desired = (0, 0, 1, 1, 0, 0)
>>> for bi, bands in enumerate(((0, 1, 2, 3, 4, 5), (0, 1, 2, 4, 4.5, 5))):
...     fir_firls = signal.firls(73, bands, desired, fs=fs)
...     fir_remez = signal.remez(73, bands, desired[::2], fs=fs)
...     fir_firwin2 = signal.firwin2(73, bands, desired, fs=fs)
...     hs = list()
...     ax = axs[bi]
...     for fir in (fir_firls, fir_remez, fir_firwin2):
...         freq, response = signal.freqz(fir)
...         hs.append(ax.semilogy(0.5*fs*freq/np.pi, np.abs(response))[0])
...     for band, gains in zip(zip(bands[::2], bands[1::2]),
...                            zip(desired[::2], desired[1::2])):
...         ax.semilogy(band, np.maximum(gains, 1e-7), 'k--', linewidth=2)
...     if bi == 0:
...         ax.legend(hs, ('firls', 'remez', 'firwin2'),
...                   loc='lower center', frameon=False)
...     else:
...         ax.set_xlabel('Frequency (Hz)')
...     ax.grid(True)
...     ax.set(title='Band-pass %d-%d Hz' % bands[2:4], ylabel='Magnitude')
...
>>> fig.tight_layout()
>>> plt.show()