scipy.signal.

remez

scipy.signal.remez(numtaps, bands, желаемый, *, вес=None, тип='bandpass', maxiter=25, grid_density=16, fs=None)

Вычислить минимаксный оптимальный фильтр с использованием алгоритма обмена Ремеза.

Вычислить коэффициенты фильтра для фильтра с конечной импульсной характеристикой (КИХ), чья передаточная функция минимизирует максимальную ошибку между желаемым усилением и реализованным усилением в указанных частотных полосах с использованием алгоритма обмена Ремеза.

Параметры:

numtapsint

Желаемое количество отводов в фильтре. Количество отводов — это количество членов в фильтре или порядок фильтра плюс один.

bandsarray_like

Монотонная последовательность, содержащая границы полосы. Все элементы должны быть неотрицательными и меньше половины частоты дискретизации, заданной fs.

желаемыйarray_like

Последовательность вдвое меньше размера полос, содержащая желаемое усиление в каждой из указанных полос.

весarray_like, необязательный

Относительный вес для каждой полосы. Длина вес должна быть половиной длины bands.

тип{'bandpass', 'differentiator', 'hilbert'}, опционально

Тип фильтра:

• ‘bandpass’ : плоская характеристика в полосах пропускания. Это значение по умолчанию.

• ‘differentiator’ : частотно-пропорциональный отклик в полосах.

• ‘hilbert’фильтр с нечётной симметрией, то есть тип III

  (для чётного порядка) или типа IV (для нечётного порядка) линейно-фазовых фильтров.

maxiterint, необязательный

Максимальное количество итераций алгоритма. По умолчанию 25.

grid_densityint, необязательный

Плотность сетки. Плотная сетка, используемая в remez имеет размер (numtaps + 1) * grid_density. По умолчанию 16.

fsfloat, опционально

Частота дискретизации сигнала. По умолчанию равна 1.

Возвращает:

выходndarray

Массив ранга 1, содержащий коэффициенты оптимального (в смысле минимакса) фильтра.

Смотрите также

firls

firwin

firwin2

minimum_phase

Ссылки

[1]

J. H. McClellan и T. W. Parks, “A unified approach to the design of optimum FIR linear phase digital filters”, IEEE Trans. Circuit Theory, vol. CT-20, pp. 697-701, 1973.

[2]

J. H. McClellan, T. W. Parks и L. R. Rabiner, «A Computer Program for Designing Optimum FIR Linear Phase Digital Filters», IEEE Trans. Audio Electroacoust., vol. AU-21, pp. 506-525, 1973.

Примеры

Попробуйте в вашем браузере!

В этих примерах, remez используется для проектирования фильтров нижних, верхних, полосовых и режекторных частот. Параметры, определяющие каждый фильтр, включают порядок фильтра, границы полос, ширины переходных областей границ, желаемые усиления в каждой полосе и частоту дискретизации.

Мы будем использовать частоту дискретизации 22050 Гц во всех примерах. В каждом примере желаемое усиление в каждой полосе равно либо 0 (для полосы задерживания), либо 1 (для полосы пропускания).

freqz используется для вычисления частотной характеристики каждого фильтра, и вспомогательная функция plot_response определенный ниже используется для построения графика отклика.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> fs = 22050   # Sample rate, Hz

>>> def plot_response(w, h, title):
...     "Utility function to plot response functions"
...     fig = plt.figure()
...     ax = fig.add_subplot(111)
...     ax.plot(w, 20*np.log10(np.abs(h)))
...     ax.set_ylim(-40, 5)
...     ax.grid(True)
...     ax.set_xlabel('Frequency (Hz)')
...     ax.set_ylabel('Gain (dB)')
...     ax.set_title(title)

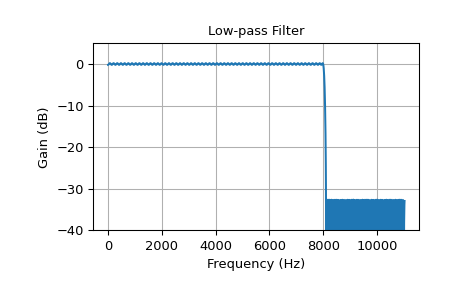
Первый пример — фильтр нижних частот с частотой среза 8 кГц. Длина фильтра составляет 325, а ширина перехода от полосы пропускания к полосе задерживания — 100 Гц.

>>> cutoff = 8000.0    # Desired cutoff frequency, Hz
>>> trans_width = 100  # Width of transition from pass to stop, Hz
>>> numtaps = 325      # Size of the FIR filter.
>>> taps = signal.remez(numtaps, [0, cutoff, cutoff + trans_width, 0.5*fs],
...                     [1, 0], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Low-pass Filter")
>>> plt.show()

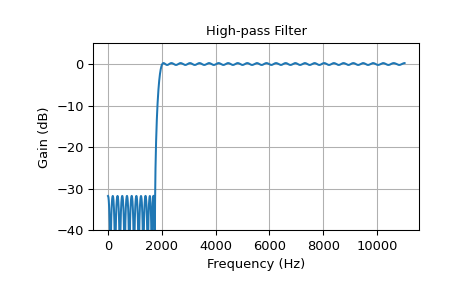
Этот пример показывает фильтр верхних частот:

>>> cutoff = 2000.0    # Desired cutoff frequency, Hz
>>> trans_width = 250  # Width of transition from pass to stop, Hz
>>> numtaps = 125      # Size of the FIR filter.
>>> taps = signal.remez(numtaps, [0, cutoff - trans_width, cutoff, 0.5*fs],
...                     [0, 1], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "High-pass Filter")
>>> plt.show()

Этот пример показывает полосовой фильтр с полосой пропускания от 2 кГц до 5 кГц. Ширина перехода составляет 260 Гц, а длина фильтра равна 63, что меньше, чем в других примерах:

>>> band = [2000, 5000]  # Desired pass band, Hz
>>> trans_width = 260    # Width of transition from pass to stop, Hz
>>> numtaps = 63         # Size of the FIR filter.
>>> edges = [0, band[0] - trans_width, band[0], band[1],
...          band[1] + trans_width, 0.5*fs]
>>> taps = signal.remez(numtaps, edges, [0, 1, 0], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Band-pass Filter")
>>> plt.show()

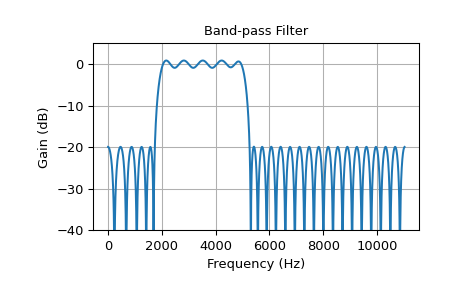
Низкий порядок приводит к более высокой пульсации и менее крутым переходам.

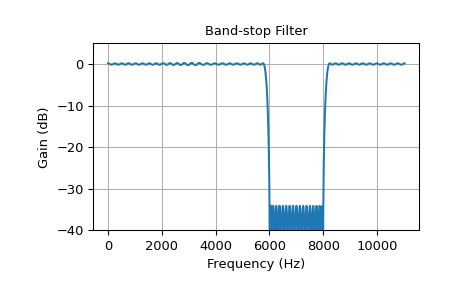
Следующий пример показывает полосно-заграждающий фильтр.

>>> band = [6000, 8000]  # Desired stop band, Hz
>>> trans_width = 200    # Width of transition from pass to stop, Hz
>>> numtaps = 175        # Size of the FIR filter.
>>> edges = [0, band[0] - trans_width, band[0], band[1],
...          band[1] + trans_width, 0.5*fs]
>>> taps = signal.remez(numtaps, edges, [1, 0, 1], fs=fs)
>>> w, h = signal.freqz(taps, [1], worN=2000, fs=fs)
>>> plot_response(w, h, "Band-stop Filter")
>>> plt.show()

НазадОткрыть во вкладке