scipy.signal.

freqz_sos

scipy.signal.freqz_sos(sos, worN=512, целый=False, fs=6.283185307179586)

Вычислите частотную характеристику цифрового фильтра в формате SOS.

Учитывая sos, массив формы (n, 6) из звеньев второго порядка цифрового фильтра, вычислить частотную характеристику системной функции:

       B0(z)   B1(z)         B{n-1}(z)
H(z) = ----- * ----- * ... * ---------
       A0(z)   A1(z)         A{n-1}(z)

для z = exp(omega*1j), где B{k}(z) и A{k}(z) — числитель и знаменатель передаточной функции k-го звена второго порядка.

Параметры:

sosarray_like

Массив коэффициентов фильтра второго порядка, должен иметь форму (n_sections, 6). Каждая строка соответствует звеньям второго порядка, с первыми тремя столбцами, предоставляющими коэффициенты числителя, и последними тремя — коэффициенты знаменателя.

worN{None, int, array_like}, optional

Если указано одно целое число, то вычисление выполняется на этом количестве частот (по умолчанию N=512). Использование числа, удобного для вычислений БПФ, может ускорить вычисления (см. Примечания в freqz).

Если передан array_like, вычисляет отклик на заданных частотах (должен быть 1-D). Они в тех же единицах, что и fs.

целыйbool, необязательно

Обычно частоты вычисляются от 0 до частоты Найквиста, fs/2 (верхняя половина единичной окружности). Если целый is True, вычислять частоты от 0 до fs.

fsfloat, опционально

Частота дискретизации цифровой системы. По умолчанию 2*pi радиан/отсчёт (так что w находится в диапазоне от 0 до pi).

Добавлено в версии 1.2.0.

Возвращает:

wndarray

Частоты, на которых h было вычислено, в тех же единицах, что и fs. По умолчанию, w нормализован в диапазон [0, pi) (радиан/образец).

hndarray

Частотная характеристика в виде комплексных чисел.

Смотрите также

freqz, sosfilt, sosfreqz

Примечания

Эта функция раньше называлась sosfreqz в старых версиях (≥ 0.19.0)

Добавлено в версии 1.15.0.

Примеры

Попробуйте в вашем браузере!

Спроектируйте полосовой фильтр 15-го порядка в формате SOS.

>>> from scipy import signal
>>> import numpy as np
>>> sos = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass',
...                    output='sos')

Вычислить частотную характеристику в 1500 точках от постоянного тока до частоты Найквиста.

>>> w, h = signal.freqz_sos(sos, worN=1500)

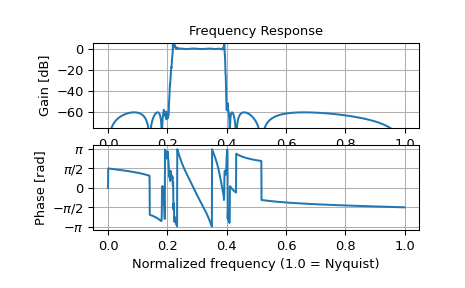
Построить график отклика.

>>> import matplotlib.pyplot as plt
>>> plt.subplot(2, 1, 1)
>>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5))
>>> plt.plot(w/np.pi, db)
>>> plt.ylim(-75, 5)
>>> plt.grid(True)
>>> plt.yticks([0, -20, -40, -60])
>>> plt.ylabel('Gain [dB]')
>>> plt.title('Frequency Response')
>>> plt.subplot(2, 1, 2)
>>> plt.plot(w/np.pi, np.angle(h))
>>> plt.grid(True)
>>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi],
...            [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$'])
>>> plt.ylabel('Phase [rad]')
>>> plt.xlabel('Normalized frequency (1.0 = Nyquist)')
>>> plt.show()

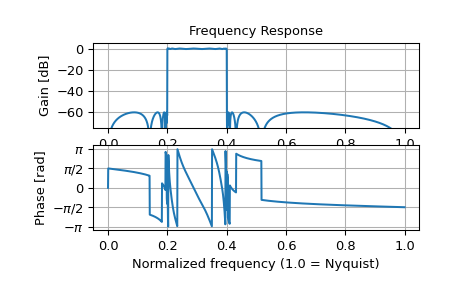
Если тот же фильтр реализован как единая передаточная функция, численная ошибка искажает частотную характеристику:

>>> b, a = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass',
...                    output='ba')
>>> w, h = signal.freqz(b, a, worN=1500)
>>> plt.subplot(2, 1, 1)
>>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5))
>>> plt.plot(w/np.pi, db)
>>> plt.ylim(-75, 5)
>>> plt.grid(True)
>>> plt.yticks([0, -20, -40, -60])
>>> plt.ylabel('Gain [dB]')
>>> plt.title('Frequency Response')
>>> plt.subplot(2, 1, 2)
>>> plt.plot(w/np.pi, np.angle(h))
>>> plt.grid(True)
>>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi],
...            [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$'])
>>> plt.ylabel('Phase [rad]')
>>> plt.xlabel('Normalized frequency (1.0 = Nyquist)')
>>> plt.show()

НазадОткрыть во вкладке