scipy.signal.

freqz#

scipy.signal.freqz(b, a=1, worN=512, целый=False, plot=None, fs=6.283185307179586, include_nyquist=False)[источник]#

Вычислить частотную характеристику цифрового фильтра.

Для числителя M-го порядка b и знаменатель N-го порядка a цифрового фильтра, вычислите его частотную характеристику:

            jw                 -jw              -jwM
   jw    B(e  )    b[0] + b[1]e    + ... + b[M]e
H(e  ) = ------ = -----------------------------------
            jw                 -jw              -jwN
         A(e  )    a[0] + a[1]e    + ... + a[N]e
Параметры:
barray_like

Числитель линейного фильтра. Если b имеет размерность больше 1, предполагается, что коэффициенты хранятся в первом измерении, и b.shape[1:], a.shape[1:], и форма массива частот должна быть совместима для трансляции.

aarray_like

Знаменатель линейного фильтра. Если b имеет размерность больше 1, предполагается, что коэффициенты хранятся в первом измерении, и b.shape[1:], a.shape[1:], и форма массива частот должна быть совместима для трансляции.

worN{None, int, array_like}, optional

Если одно целое число, то вычисляет на таком количестве частот (по умолчанию N=512). Это удобная альтернатива:

np.linspace(0, fs if whole else fs/2, N, endpoint=include_nyquist)

Использование числа, удобного для вычислений БПФ, может привести к более быстрым вычислениям (см. примечания).

Если передан array_like, вычислить отклик на заданных частотах. Они в тех же единицах, что и fs.

целыйbool, необязательно

Обычно частоты вычисляются от 0 до частоты Найквиста, fs/2 (верхняя половина единичной окружности). Если целый равно True, вычислять частоты от 0 до fs. Игнорируется, если worN является array_like.

plotcallable

Вызываемый объект, принимающий два аргумента. Если задан, возвращаемые параметры w и h передаются в plot. Полезно для построения частотной характеристики внутри freqz.

fsfloat, опционально

Частота дискретизации цифровой системы. По умолчанию 2*pi радиан/отсчёт (так что w находится в диапазоне от 0 до pi).

Добавлено в версии 1.2.0.

include_nyquistbool, необязательно

Если целый равно False и worN является целым числом, установка include_nyquist в True включает последнюю частоту (частота Найквиста) и в противном случае игнорируется.

Добавлено в версии 1.5.0.

Возвращает:
wndarray

Частоты, на которых h было вычислено, в тех же единицах, что и fs. По умолчанию, w нормализован в диапазон [0, pi) (радиан/образец).

hndarray

Частотная характеристика в виде комплексных чисел.

Смотрите также

freqz_zpk
freqz_sos

Примечания

Используя Matplotlib matplotlib.pyplot.plot функцию как вызываемый объект для plot дает неожиданные результаты, так как это отображает действительную часть комплексной передаточной функции, а не амплитуду. Попробуйте lambda w, h: plot(w, np.abs(h)).

Прямое вычисление через (R)FFT используется для вычисления частотной характеристики, когда выполняются следующие условия:

  1. Целочисленное значение задано для worN.

  2. worN быстро вычисляется через БПФ (т.е., next_fast_len(worN) равно worN).

  3. Коэффициенты знаменателя являются единственным значением (a.shape[0] == 1).

  4. worN по крайней мере такой же длины, как коэффициенты числителя (worN >= b.shape[0]).

  5. Если b.ndim > 1, затем b.shape[-1] == 1.

Для длинных FIR-фильтров подход с использованием БПФ может иметь меньшую ошибку и быть значительно быстрее, чем эквивалентный прямой полиномиальный расчет.

Примеры

>>> from scipy import signal
>>> import numpy as np
>>> taps, f_c = 80, 1.0  # number of taps and cut-off frequency
>>> b = signal.firwin(taps, f_c, window=('kaiser', 8), fs=2*np.pi)
>>> w, h = signal.freqz(b)

>>> import matplotlib.pyplot as plt
>>> fig, ax1 = plt.subplots(tight_layout=True)
>>> ax1.set_title(f"Frequency Response of {taps} tap FIR Filter" +
...               f"($f_c={f_c}$ rad/sample)")
>>> ax1.axvline(f_c, color='black', linestyle=':', linewidth=0.8)
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'C0')
>>> ax1.set_ylabel("Amplitude in dB", color='C0')
>>> ax1.set(xlabel="Frequency in rad/sample", xlim=(0, np.pi))

>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'C1')
>>> ax2.set_ylabel('Phase [rad]', color='C1')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> plt.show()
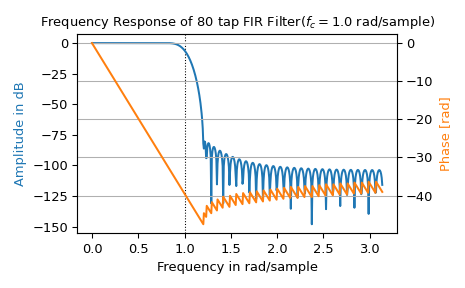
../../_images/scipy-signal-freqz-1_00_00.png

Примеры вещания

Предположим, у нас есть два FIR-фильтра, коэффициенты которых хранятся в строках массива формы (2, 25). Для этой демонстрации мы используем случайные данные:

>>> rng = np.random.default_rng()
>>> b = rng.random((2, 25))

Чтобы вычислить частотную характеристику для этих двух фильтров одним вызовом функции freqz, мы должны передать b.T, потому что freqz ожидает, что первая ось содержит коэффициенты. Затем мы должны расширить форму с помощью тривиального измерения длины 1, чтобы разрешить трансляцию с массивом частот. То есть мы передаем b.T[..., np.newaxis], который имеет форму (25, 2, 1):

>>> w, h = signal.freqz(b.T[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)

Теперь предположим, что у нас есть две передаточные функции с одинаковыми коэффициентами числителя b = [0.5, 0.5]. Коэффициенты для двух знаменателей хранятся в первом измерении 2-D массива a:

a = [   1      1  ]
    [ -0.25, -0.5 ]

>>> b = np.array([0.5, 0.5])
>>> a = np.array([[1, 1], [-0.25, -0.5]])

Только a имеет более 1 измерения. Чтобы сделать его совместимым для вещания с частотами, мы расширяем его тривиальным измерением в вызове freqz:

>>> w, h = signal.freqz(b, a[..., np.newaxis], worN=1024)
>>> w.shape
(1024,)
>>> h.shape
(2, 1024)
На этой странице