scipy.signal.

lombscargle#

scipy.signal.lombscargle(x, y, freqs, precenter=False, нормализовать=False, *, веса=None, floating_mean=False)[источник]#

Вычислить обобщенный периодограмму Ломба-Скаргла.

Периодограмма Ломба-Скаргла была разработана Ломбом [1] и далее расширен Скарглом [2] для поиска и проверки значимости слабых периодических сигналов с неравномерной временной выборкой. Используемый здесь алгоритм основан на взвешенном методе наименьших квадратов вида y(ω) = a*cos(ω*x) + b*sin(ω*x) + c, где подгонка рассчитывается для каждой частоты независимо. Этот алгоритм был разработан Цехмейстером и Кюрстером, который улучшает периодограмму Ломба-Скаргла, позволяя взвешивать отдельные выборки и рассчитывать неизвестное смещение y (также называемое моделью "плавающего среднего"). [3]. Для получения дополнительных сведений и практических соображений см. отличную ссылку на периодограмму Ломба-Скаргла [4].

Когда нормализовать равно False (или "power") (по умолчанию) вычисленный периодограмм не нормализован, он принимает значение (A**2) * N/4 для гармонического сигнала с амплитудой A для достаточно больших N. Где N - длина x или y.

Когда нормализовать равно True (или 'normalize'), вычисленный периодограмм нормализуется по остаткам данных вокруг постоянной референсной модели (на нуле).

Когда нормализовать является "амплитудой", вычисленный периодограмма представляет комплексное представление амплитуды и фазы.

Входные массивы должны быть одномерными с вещественным типом данных с плавающей точкой, которые преобразуются в массивы float64 перед обработкой.

Параметры:

xarray_like: Времена выборки.
yarray_like: Значения измерений. Предполагается, что значения имеют базовый уровень y = 0. Если возможно смещение по y, рекомендуется установить floating_mean в True.
freqsarray_like: Угловые частоты (например, имеющие единицу рад/с=2π/с для x имея единицу с) для выходной периодограммы. Частоты обычно >= 0, так как любой пик на -freq также будет существовать в +freq.
precenterbool, необязательно: Предварительно центрировать значения измерений, вычитая среднее, если True. Это устаревший параметр и необязательный, если floating_mean равно True.
нормализоватьbool | str, optional: Вычисление нормализованного или комплексного (амплитуда + фаза) периодограммы. Допустимые опции: False/"power", True/"normalize", или "amplitude".
весаarray_like, необязательный: Веса для каждой выборки. Веса должны быть неотрицательными.
floating_meanbool, необязательно: Определяет смещение по y для каждой частоты независимо, если True. Иначе смещение по y предполагается равным 0.

Возвращает:

pgramarray_like: Периодограмма Ломба-Скаргла.

Вызывает:

ValueError: Если любой из входных массивов x, y, freqs или weights не является одномерным, или если любой из них имеет нулевую длину. Или если входные массивы x, y и weights не имеют одинаковой формы друг с другом.
ValueError: Если любой вес < 0, или сумма весов <= 0.
ValueError: Если параметр normalize не является одним из разрешённых вариантов.

Смотрите также

periodogram: Спектральная плотность мощности с использованием периодограммы
welch: Спектральная плотность мощности методом Уэлча
csd: Спектральная плотность мощности по методу Уэлча

Примечания

Используемый алгоритм не будет автоматически учитывать любое неизвестное смещение по y, если только floating_mean не установлен в True. Поэтому для большинства случаев использования, если возможно смещение по y, рекомендуется установить floating_mean в True. Если precenter установлен в True, он выполняет операцию y -= y.mean(). Однако precenter — это устаревший параметр, и он не нужен, когда floating_mean равен True. Более того, среднее значение, удаляемое precenter, не учитывает веса выборок и не исправит любое смещение из-за последовательно пропущенных наблюдений на пиках и/или впадинах. Когда параметр normalize равен "amplitude", для любой частоты в freqs, которая ниже (2*pi)/(x.max() - x.min()), предсказанная амплитуда будет стремиться к бесконечности. Понятие «предела частоты Найквиста» (см. теорему отсчётов Найквиста-Шеннона) обычно неприменимо к неравномерно дискретизированным данным. Поэтому для неравномерно дискретизированных данных допустимые частоты в freqs часто могут быть намного выше ожидаемых.

Ссылки

[1]

N.R. Lomb «Least-squares frequency analysis of unequally spaced data», Astrophysics and Space Science, vol 39, pp. 447-462, 1976 DOI:10.1007/bf00648343

[2]

J.D. Scargle «Исследования в анализе астрономических временных рядов. II - Статистические аспекты спектрального анализа неравномерно распределенных данных», The Astrophysical Journal, том 263, стр. 835-853, 1982 DOI:10.1086/160554

[3]

M. Zechmeister и M. Kürster, “The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms,” Astronomy and Astrophysics, vol. 496, pp. 577-584, 2009 DOI:10.1051/0004-6361:200811296

[4]

J.T. VanderPlas, "Understanding the Lomb-Scargle Periodogram," The Astrophysical Journal Supplement Series, vol. 236, no. 1, p. 16, May 2018 DOI:10.3847/1538-4365/aab766

Примеры

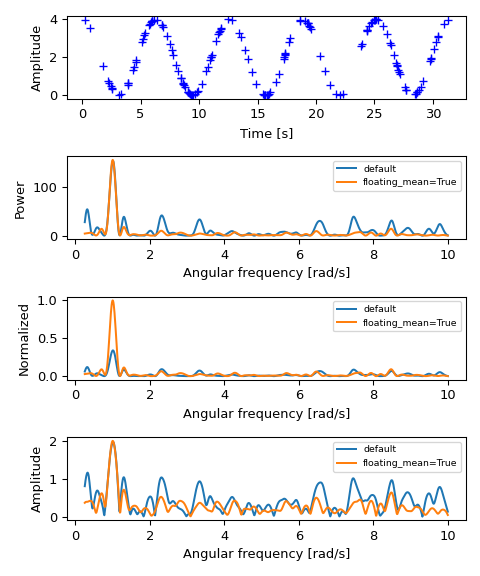
>>> import numpy as np
>>> rng = np.random.default_rng()

Сначала определим некоторые входные параметры для сигнала:

>>> A = 2.  # amplitude
>>> c = 2.  # offset
>>> w0 = 1.  # rad/sec
>>> nin = 150
>>> nout = 1002

Случайная генерация временных меток выборок:

>>> x = rng.uniform(0, 10*np.pi, nin)

Построить синусоиду для выбранных временных точек:

>>> y = A * np.cos(w0*x) + c

Определите массив частот, для которых вычисляется периодограмма:

>>> w = np.linspace(0.25, 10, nout)

Вычислить периодограмму Ломба-Скаргла для каждого из вариантов нормализации:

>>> from scipy.signal import lombscargle
>>> pgram_power = lombscargle(x, y, w, normalize=False)
>>> pgram_norm = lombscargle(x, y, w, normalize=True)
>>> pgram_amp = lombscargle(x, y, w, normalize='amplitude')
...
>>> pgram_power_f = lombscargle(x, y, w, normalize=False, floating_mean=True)
>>> pgram_norm_f = lombscargle(x, y, w, normalize=True, floating_mean=True)
>>> pgram_amp_f = lombscargle(x, y, w, normalize='amplitude', floating_mean=True)

Теперь построить график входных данных:

>>> import matplotlib.pyplot as plt
>>> fig, (ax_t, ax_p, ax_n, ax_a) = plt.subplots(4, 1, figsize=(5, 6))
>>> ax_t.plot(x, y, 'b+')
>>> ax_t.set_xlabel('Time [s]')
>>> ax_t.set_ylabel('Amplitude')

Затем построить периодограмму для каждого из вариантов нормализации, а также с и без floating_mean=True:

>>> ax_p.plot(w, pgram_power, label='default')
>>> ax_p.plot(w, pgram_power_f, label='floating_mean=True')
>>> ax_p.set_xlabel('Angular frequency [rad/s]')
>>> ax_p.set_ylabel('Power')
>>> ax_p.legend(prop={'size': 7})
...
>>> ax_n.plot(w, pgram_norm, label='default')
>>> ax_n.plot(w, pgram_norm_f, label='floating_mean=True')
>>> ax_n.set_xlabel('Angular frequency [rad/s]')
>>> ax_n.set_ylabel('Normalized')
>>> ax_n.legend(prop={'size': 7})
...
>>> ax_a.plot(w, np.abs(pgram_amp), label='default')
>>> ax_a.plot(w, np.abs(pgram_amp_f), label='floating_mean=True')
>>> ax_a.set_xlabel('Angular frequency [rad/s]')
>>> ax_a.set_ylabel('Amplitude')
>>> ax_a.legend(prop={'size': 7})
...
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-lombscargle-1.png