scipy.signal.

csd#

scipy.signal.csd(x, y, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', return_onesided=True, масштабирование='density', ось=-1, среднее='mean')[источник]#

Оценить взаимную спектральную плотность мощности, Pxy, методом Уэлча.

Параметры:

xarray_like: Временной ряд значений измерений
yarray_like: Временной ряд значений измерений
fsfloat, опционально: Частота дискретизации x и y временные ряды. По умолчанию равно 1.0.
windowstr или tuple или array_like, опционально: Желаемое окно для использования. Если window является строкой или кортежем, он передаётся в get_window для генерации значений окна, которые по умолчанию являются DFT-чётными. См. get_window для списка окон и требуемых параметров. Если window если это array_like, он будет использоваться напрямую как окно, и его длина должна быть nperseg. По умолчанию используется окно Ханна.
npersegint, необязательный: Длина каждого сегмента. По умолчанию None, но если window является строкой или кортежем, устанавливается в 256, а если window является array_like, устанавливается в длину окна.
noverlap: int, optional: Количество точек перекрытия между сегментами. Если None, noverlap = nperseg // 2. По умолчанию None и может не быть больше чем nperseg.
nfftint, необязательный: Длина БПФ, используемая, если требуется дополненное нулями БПФ. Если None, длина БПФ равна nperseg. По умолчанию None.
detrendstr или функция или False, опционально: Определяет, как удалять тренд в каждом сегменте. Если detrend является строкой, она передается как тип аргумент для detrend функция. Если это функция, она принимает сегмент и возвращает сегмент с удалённым трендом. Если detrend является False, детрендинг не выполняется. По умолчанию 'constant'.
return_onesidedbool, необязательно: Если True, возвращает односторонний спектр для реальных данных. Если False возвращает двусторонний спектр. По умолчанию True, но для комплексных данных всегда возвращается двусторонний спектр.
масштабирование{ 'density', 'spectrum' }, опционально: Выбирает между вычислением спектральной плотности мощности ('density'), где Pxy имеет единицы измерения V**2/Гц и вычисляет взаимный спектр ('спектр'), где Pxy имеет единицы измерения V**2, если x и y измеряются в В и fs измеряется в Гц. По умолчанию 'density'
осьint, необязательный: Ось, по которой вычисляется CSD для обоих входов; по умолчанию — по последней оси (т.е. axis=-1).
среднее{ ‘mean’, ‘median’ }, опционально: Метод усреднения периодограмм. Если спектр комплексный, усреднение вычисляется отдельно для действительной и мнимой частей. По умолчанию 'mean'.

Добавлено в версии 1.2.0.

Возвращает:

fndarray: Массив частот выборки.
Pxyndarray: Кросс-спектральная плотность или кросс-спектр мощности x,y.

Смотрите также

periodogram: Простой, опционально модифицированный периодограмм
lombscargle: Периодограмма Ломба-Скаргла для неравномерно дискретизированных данных
welch: Спектральная плотность мощности по методу Уэлча. [Эквивалентно csd(x,x)]
coherence: Квадрат модуля когерентности методом Уэлча.

Примечания

По соглашению, Pxy вычисляется с использованием сопряжённого БПФ X, умноженного на БПФ Y.

Если входные ряды различаются по длине, более короткий ряд будет дополнен нулями для соответствия.

Подходящее количество перекрытия будет зависеть от выбора окна и ваших требований. Для окна Ханна по умолчанию перекрытие в 50% является разумным компромиссом между точной оценкой мощности сигнала и избеганием повторного учета данных. Более узкие окна могут требовать большего перекрытия.

Отношение кросс-спектра (scaling='spectrum') делённое на кросс-спектральную плотность (scaling='density') является постоянным множителем sum(abs(window)**2)*fs / abs(sum(window))**2. Если return_onesided является True, значения отрицательных частот добавляются к значениям соответствующих положительных.

Обратитесь к Спектральный анализ раздел Руководство пользователя SciPy для обсуждения масштабирований спектральной плотности и (амплитудного) спектра.

Метод Уэлча может быть интерпретирован как усреднение по временным срезам (кросс-) спектрограммы. Внутренне эта функция использует ShortTimeFFT для определения требуемой (кросс-) спектрограммы. Пример ниже показывает, что легко вычислить Pxy напрямую с ShortTimeFFT. Однако, существуют некоторые заметные различия в поведении ShortTimeFFT:

Нет прямого ShortTimeFFT эквивалент для csd комбинация параметров return_onesided=True, scaling='density', поскольку fft_mode='onesided2X' требует 'psd' масштабирование. Это связано с csd возвращая удвоенный квадрат величины в этом случае, что не имеет разумной интерпретации.
ShortTimeFFT использует float64 / complex128 внутренне, что связано с поведением используемого fft модуль. Таким образом, это типы данных, возвращаемые в результате. csd функция приводит возвращаемые значения к float32 / complex64 если входные данные float32 / complex64 также.
The csd функция вычисляет np.conj(Sx[q,p]) * Sy[q,p], тогда как spectrogram вычисляет Sx[q,p] * np.conj(Sy[q,p]) где Sx[q,p], Sy[q,p] являются STFT для x и y. Также, позиционирование окна отличается.

Добавлено в версии 0.16.0.

Ссылки

[1]

P. Welch, "Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени коротких модифицированных периодограмм", IEEE Trans. Audio Electroacoust. том 15, стр. 70-73, 1967.

[2]

Rabiner, Lawrence R., и B. Gold. "Теория и применение цифровой обработки сигналов" Prentice-Hall, стр. 414-419, 1975

Примеры

Следующий пример строит график взаимной спектральной плотности мощности двух сигналов с некоторыми общими особенностями:

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
...
... # Generate two test signals with some common features:
>>> N, fs = 100_000, 10e3  # number of samples and sampling frequency
>>> amp, freq = 20, 1234.0  # amplitude and frequency of utilized sine signal
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> b, a = signal.butter(2, 0.25, 'low')
>>> x = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> y = signal.lfilter(b, a, x)
>>> x += amp*np.sin(2*np.pi*freq*time)
>>> y += rng.normal(scale=0.1*np.sqrt(noise_power), size=time.shape)
...
... # Compute and plot the magnitude of the cross spectral density:
>>> nperseg, noverlap, win = 1024, 512, 'hann'
>>> f, Pxy = signal.csd(x, y, fs, win, nperseg, noverlap)
>>> fig0, ax0 = plt.subplots(tight_layout=True)
>>> ax0.set_title(f"CSD ({win.title()}-window, {nperseg=}, {noverlap=})")
>>> ax0.set(xlabel="Frequency $f$ in kHz", ylabel="CSD Magnitude in V²/Hz")
>>> ax0.semilogy(f/1e3, np.abs(Pxy))
>>> ax0.grid()
>>> plt.show()

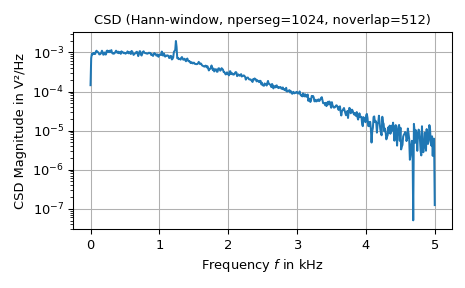
../../_images/scipy-signal-csd-1_00_00.png

Перекрёстная спектральная плотность вычисляется путём усреднения по временным срезам спектрограммы:

>>> SFT = signal.ShortTimeFFT.from_window('hann', fs, nperseg, noverlap,
...                                       scale_to='psd', fft_mode='onesided2X',
...                                       phase_shift=None)
>>> Sxy1 = SFT.spectrogram(y, x, detr='constant', k_offset=nperseg//2,
...                        p0=0, p1=(N-noverlap) // SFT.hop)
>>> Pxy1 = Sxy1.mean(axis=-1)
>>> np.allclose(Pxy, Pxy1)  # same result as with csd()
True

Как обсуждается в разделе Примечания, результаты использования подхода, аналогичного приведённому выше фрагменту кода, и csd функция может отклоняться из-за особенностей реализации.

Обратите внимание, что приведенный выше фрагмент кода можно легко адаптировать для определения других статистических свойств, кроме среднего значения.