scipy.signal.

periodogram#

scipy.signal.periodogram(x, fs=1.0, window='boxcar', nfft=None, detrend='constant', return_onesided=True, масштабирование='density', ось=-1)[источник]#

Оцените спектральную плотность мощности с использованием периодограммы.

Параметры:

xarray_like: Временной ряд значений измерений
fsfloat, опционально: Частота дискретизации x временной ряд. По умолчанию 1.0.
windowstr или tuple или array_like, опционально: Желаемое окно для использования. Если window является строкой или кортежем, он передаётся в get_window для генерации значений окна, которые по умолчанию являются DFT-чётными. См. get_window для списка окон и требуемых параметров. Если window если это array_like, он будет использован напрямую как окно, и его длина должна быть равна длине оси, по которой вычисляется периодограмма. По умолчанию 'boxcar'.
nfftint, необязательный: Длина используемого БПФ. Если None длину x будет использоваться.
detrendstr или функция или False, опционально: Определяет, как удалять тренд в каждом сегменте. Если detrend является строкой, она передается как тип аргумент для detrend функция. Если это функция, она принимает сегмент и возвращает сегмент с удалённым трендом. Если detrend является False, детрендинг не выполняется. По умолчанию 'constant'.
return_onesidedbool, необязательно: Если True, возвращает односторонний спектр для реальных данных. Если False возвращает двусторонний спектр. По умолчанию True, но для комплексных данных всегда возвращается двусторонний спектр.
масштабирование{ 'density', 'spectrum' }, опционально: Выбор между вычислением спектральной плотности мощности ('density') где Pxx имеет единицы измерения В²/Гц, и вычисление квадрата амплитудного спектра (‘спектр’), где Pxx имеет единицы измерения V², если x измеряется в В, а fs измеряется в Гц. По умолчанию ‘density’
осьint, необязательный: Ось, вдоль которой вычисляется периодограмма; по умолчанию по последней оси (т.е. axis=-1).

Возвращает:

fndarray: Массив частот выборки.
Pxxndarray: Спектральная плотность мощности или спектр мощности x.

Смотрите также

welch: Оценка спектральной плотности мощности методом Уэлча
lombscargle: Периодограмма Ломба-Скаргла для неравномерно дискретизированных данных

Примечания

Отношение квадрата величины (scaling='spectrum') деленная на спектральную плотность мощности (scaling='density') является постоянным множителем sum(abs(window)**2)*fs / abs(sum(window))**2. Если return_onesided является True, значения отрицательных частот добавляются к значениям соответствующих положительных.

Обратитесь к Спектральный анализ раздел Руководство пользователя SciPy для обсуждения масштабирования спектральной плотности мощности и спектра амплитуды (в квадрате).

Добавлено в версии 0.12.0.

Примеры

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Сгенерировать тестовый сигнал, синусоиду 2 Vrms на частоте 1234 Гц, искажённую белым шумом 0.001 V**2/Гц, дискретизированную на 10 кГц.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2*np.sqrt(2)
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> x = amp*np.sin(2*np.pi*freq*time)
>>> x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)

Вычислить и построить спектральную плотность мощности.

>>> f, Pxx_den = signal.periodogram(x, fs)
>>> plt.semilogy(f, Pxx_den)
>>> plt.ylim([1e-7, 1e2])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('PSD [V**2/Hz]')
>>> plt.show()

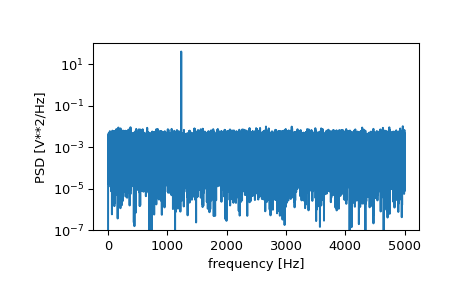
../../_images/scipy-signal-periodogram-1_00_00.png

Если усреднить вторую половину спектральной плотности, чтобы исключить пик, можно восстановить мощность шума сигнала.

>>> np.mean(Pxx_den[25000:])
0.000985320699252543

Теперь вычислите и постройте спектр мощности.

>>> f, Pxx_spec = signal.periodogram(x, fs, 'flattop', scaling='spectrum')
>>> plt.figure()
>>> plt.semilogy(f, np.sqrt(Pxx_spec))
>>> plt.ylim([1e-4, 1e1])
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Linear spectrum [V RMS]')
>>> plt.show()

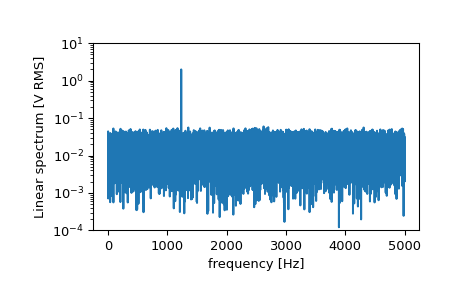
../../_images/scipy-signal-periodogram-1_01_00.png

Высота пика в спектре мощности является оценкой среднеквадратичной амплитуды.

>>> np.sqrt(Pxx_spec.max())
2.0077340678640727