scipy.special.

chebyt

scipy.special.chebyt(n, монический=False)

Полином Чебышёва первого рода.

Определяется как решение уравнения

\[(1 - x^2)\frac{d^2}{dx^2}T_n - x\frac{d}{dx}T_n + n^2T_n = 0;\]

\(T_n\) является полиномом степени \(n\).

Параметры:

nint

Степень полинома.

моническийbool, необязательно

Если True, масштабировать старший коэффициент до 1. По умолчанию False.

Возвращает:

Torthopoly1d

Полином Чебышёва первого рода.

Смотрите также

chebyu

Полином Чебышёва второго рода.

Примечания

Полиномы \(T_n\) ортогональны на \([-1, 1]\) с весовой функцией \((1 - x^2)^{-1/2}\).

Ссылки

[AS]

Милтон Абрамовиц и Ирен А. Стегун, ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Dover, 1972.

Примеры

Попробуйте в вашем браузере!

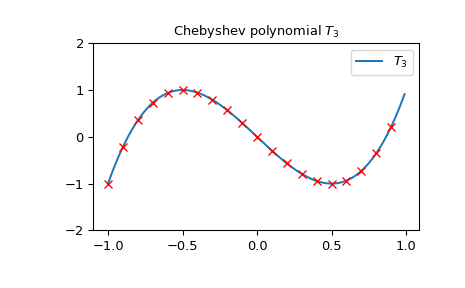
Полиномы Чебышёва первого рода порядка \(n\) может быть получен как определитель конкретного \(n \times n\) матрицы. В качестве примера мы можем проверить, как точки, полученные из определителя следующей \(3 \times 3\) матрица точно лежит на \(T_3\):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.linalg import det
>>> from scipy.special import chebyt
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-2.0, 2.0)
>>> ax.set_title(r'Chebyshev polynomial $T_3$')
>>> ax.plot(x, chebyt(3)(x), label=rf'$T_3$')
>>> for p in np.arange(-1.0, 1.0, 0.1):
...     ax.plot(p,
...             det(np.array([[p, 1, 0], [1, 2*p, 1], [0, 1, 2*p]])),
...             'rx')
>>> plt.legend(loc='best')
>>> plt.show()

Они также связаны с полиномами Якоби \(P_n^{(-0.5, -0.5)}\) через соотношение:

\[P_n^{(-0.5, -0.5)}(x) = \frac{1}{4^n} \binom{2n}{n} T_n(x)\]

Давайте проверим это для \(n = 3\):

>>> from scipy.special import binom
>>> from scipy.special import jacobi
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> np.allclose(jacobi(3, -0.5, -0.5)(x),
...             1/64 * binom(6, 3) * chebyt(3)(x))
True

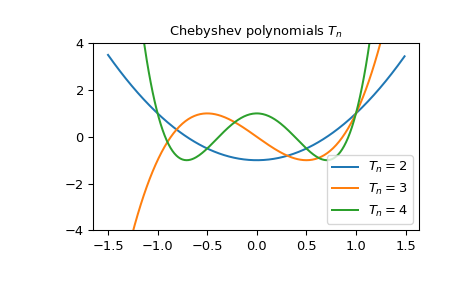
Мы можем построить график полиномов Чебышева \(T_n\) для некоторых значений параметра \(n\):

>>> x = np.arange(-1.5, 1.5, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-4.0, 4.0)
>>> ax.set_title(r'Chebyshev polynomials $T_n$')
>>> for n in np.arange(2,5):
...     ax.plot(x, chebyt(n)(x), label=rf'$T_n={n}$')
>>> plt.legend(loc='best')
>>> plt.show()

НазадОткрыть во вкладке