scipy.stats.

степень

scipy.stats.степень(тест, rvs, #18187, *, значимость=0.01, векторизованный=None, n_resamples=10000, batch=None, kwargs=None)

Смоделируйте мощность критерия проверки гипотезы при альтернативной гипотезе.

Параметры:

тестcallable

Тест гипотезы, для которого моделируется мощность. test должен быть вызываемым объектом, принимающим выборку (например. test(sample)) или len(rvs) отдельные выборки (например, test(samples1, sample2) if rvs содержит два вызываемых объекта и #18187 содержит два значения) и возвращает p-значение теста. Если векторизованный установлено в True, test также должен принимать аргумент-ключевое слово ось и быть векторизованным для выполнения теста вдоль предоставленной ось выборок. Любой вызываемый объект из scipy.stats с ось аргумент, который возвращает объект с p-значение атрибут также допустим.

rvsвызываемый объект или кортеж вызываемых объектов

Вызываемый объект или последовательность вызываемых объектов, которые генерируют случайные величины при альтернативной гипотезе. Каждый элемент rvs должен принимать аргумент ключевого слова size (например, rvs(size=(m, n))) и возвращает N-мерный массив такой формы. Если rvs является последовательностью, количество вызываемых объектов в rvs должно соответствовать количеству элементов #18187, т.е. len(rvs) == len(n_observations). Если rvs является единым вызываемым объектом, #18187 рассматривается как один элемент.

#18187кортеж целых чисел или кортеж целочисленных массивов

Если задана последовательность целых чисел, каждое из них представляет размеры выборки, передаваемой в test. Если задана последовательность целочисленных массивов, мощность моделируется для каждого набора соответствующих размеров выборки. См. Примеры.

значимостьfloat или array_like из float, по умолчанию: 0.01

Порог значимости; т.е., p-значение, ниже которого результаты проверки гипотез будут считаться свидетельством против нулевой гипотезы. Эквивалентно, допустимая частота ошибок I рода при нулевой гипотезе. Если массив, мощность моделируется для каждого порога значимости.

kwargsdict, optional

Ключевые аргументы для передачи в rvs и/или test вызываемыми объектами. Интроспекция используется для определения, какие ключевые аргументы могут быть переданы каждому вызываемому объекту. Значение, соответствующее каждому ключевому слову, должно быть массивом. Массивы должны быть совместимы для вещания друг с другом и с каждым массивом в #18187. Мощность моделируется для каждого набора соответствующих размеров выборок и аргументов. См. Примеры.

векторизованныйbool, необязательно

Если векторизованный установлено в False, test не будет передан ключевой аргумент ось и ожидается выполнение теста только для 1D выборок. Если True, test будет передан именованный аргумент ось и ожидается, что тест будет выполнен вдоль ось при передаче N-D массивов выборок. Если None (по умолчанию), векторизованный будет установлено True if axis является параметром test. Использование векторизованного теста обычно сокращает время вычислений.

n_resamplesint, по умолчанию: 10000

Количество выборок, взятых из каждого вызываемого объекта rvs. Эквивалентно, количество тестов, проведенных при альтернативной гипотезе для аппроксимации мощности.

batchint, необязательный

Количество образцов для обработки в каждом вызове test. Использование памяти пропорционально произведению batch и наибольшим размером выборки. По умолчанию равно None, в этом случае batch равно n_resamples.

Возвращает:

resPowerResult

Объект с атрибутами:

степеньfloat или ndarray

Оцененная мощность против альтернативы.

pvaluesndarray

Наблюдаемые p-значения при альтернативной гипотезе.

Примечания

Мощность моделируется следующим образом:

• Нарисовать множество случайных выборок (или наборов выборок), каждая размером(ами) указанным(ыми) в #18187, согласно альтернативе, указанной в rvs.

• Для каждого образца (или набора образцов) вычислить p-значение согласно test. Эти p-значения записаны в pvalues атрибут объекта результата.

• Вычислить долю p-значений, которые меньше значимость уровень. Это мощность, записанная в power атрибут объекта результата.

Предположим, что значимость является массивом с формой shape1, элементы из kwargs и #18187 взаимно транслируемы к форме shape2, и test возвращает массив p-значений формы shape3. Затем объект результата power атрибут будет иметь форму shape1 + shape2 + shape3, и pvalues атрибут будет иметь форму shape2 + shape3 + (n_resamples,).

Примеры

Попробуйте в вашем браузере!

Предположим, мы хотим смоделировать мощность t-критерия для независимых выборок при следующих условиях:

• Первая выборка содержит 10 наблюдений, взятых из нормального распределения со средним 0.

• Вторая выборка содержит 12 наблюдений, взятых из нормального распределения со средним 1.0.

• Порог p-значений для значимости равен 0.05.

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>>
>>> test = stats.ttest_ind
>>> n_observations = (10, 12)
>>> rvs1 = rng.normal
>>> rvs2 = lambda size: rng.normal(loc=1, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> res.power
0.6116

При размерах выборок 10 и 12 соответственно, мощность t-критерия с порогом значимости 0.05 составляет примерно 60% при выбранной альтернативе. Мы можем исследовать влияние размера выборки на мощность, передавая массивы размеров выборок.

>>> import matplotlib.pyplot as plt
>>> nobs_x = np.arange(5, 21)
>>> nobs_y = nobs_x
>>> n_observations = (nobs_x, nobs_y)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> ax = plt.subplot()
>>> ax.plot(nobs_x, res.power)
>>> ax.set_xlabel('Sample Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind` with Equal Sample Sizes')
>>> plt.show()

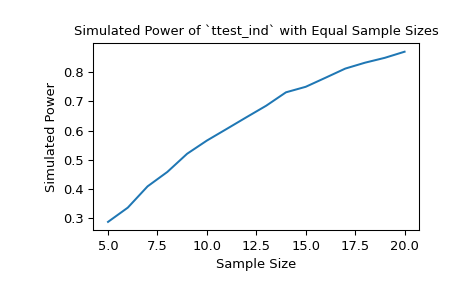
В качестве альтернативы мы можем исследовать влияние размера эффекта на мощность. В этом случае размер эффекта - это положение распределения, лежащего в основе второй выборки.

>>> n_observations = (10, 12)
>>> loc = np.linspace(0, 1, 20)
>>> rvs2 = lambda size, loc: rng.normal(loc=loc, size=size)
>>> rvs = (rvs1, rvs2)
>>> res = stats.power(test, rvs, n_observations, significance=0.05,
...                   kwargs={'loc': loc})
>>> ax = plt.subplot()
>>> ax.plot(loc, res.power)
>>> ax.set_xlabel('Effect Size')
>>> ax.set_ylabel('Simulated Power')
>>> ax.set_title('Simulated Power of `ttest_ind`, Varying Effect Size')
>>> plt.show()

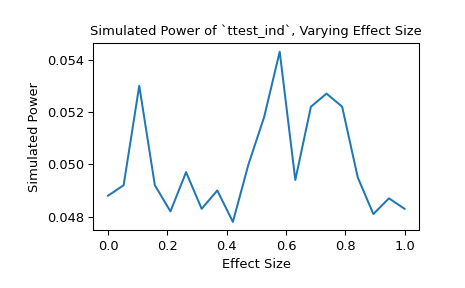
Мы также можем использовать power для оценки частоты ошибки I рода (также называемой неоднозначным термином "размер") теста и проверки соответствия номинальному уровню. Например, нулевая гипотеза jarque_bera состоит в том, что выборка была взята из распределения с той же асимметрией и эксцессом, что и нормальное распределение. Чтобы оценить частоту ошибок I рода, мы можем считать нулевую гипотезу истинной альтернатива гипотезу и рассчитать мощность.

>>> test = stats.jarque_bera
>>> n_observations = 10
>>> rvs = rng.normal
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=significance)
>>> size = res.power

Как показано ниже, уровень ошибки I рода для такого малого выборка значительно ниже номинального уровня, как упоминается в документации.

>>> ax = plt.subplot()
>>> ax.plot(significance, size)
>>> ax.plot([0, 0.1], [0, 0.1], '--')
>>> ax.set_xlabel('nominal significance level')
>>> ax.set_ylabel('estimated test size (Type I error rate)')
>>> ax.set_title('Estimated test size vs nominal significance level')
>>> ax.set_aspect('equal', 'box')
>>> ax.legend(('`ttest_1samp`', 'ideal test'))
>>> plt.show()

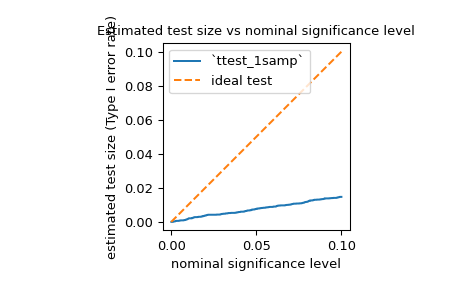
Как и следовало ожидать от такого консервативного теста, мощность довольно низкая по сравнению с некоторыми альтернативами. Например, мощность теста при альтернативе, что выборка была взята из распределения Лапласа, может быть не намного больше, чем уровень ошибки I рода.

>>> rvs = rng.laplace
>>> significance = np.linspace(0.0001, 0.1, 1000)
>>> res = stats.power(test, rvs, n_observations, significance=0.05)
>>> print(res.power)
0.0587

Это не ошибка в реализации SciPy; это просто связано с тем, что нулевое распределение тестовой статистики выводится в предположении, что размер выборки велик (т.е. стремится к бесконечности), и это асимптотическое приближение не точно для малых выборок. В таких случаях методы перевыборки и Монте-Карло (например, permutation_test, goodness_of_fit, monte_carlo_test) может быть более подходящим.

НазадОткрыть во вкладке