scipy.stats.

boxcox#

scipy.stats.boxcox(x, lmbda=None, alpha=None, оптимизатор=None)[источник]#

Возвращает набор данных, преобразованный с помощью преобразования Бокса-Кокса.

Параметры:

xndarray

Входной массив для преобразования.

Если lmbda не равно None, это псевдоним для scipy.special.boxcox. Возвращает nan, если x < 0; возвращает -inf, если x == 0 and lmbda < 0.

Если lmbda равно None, массив должен быть положительным, одномерным и непостоянным.

lmbdaскаляр, опционально

Если lmbda равно None (по умолчанию), найти значение lmbda который максимизирует функцию логарифмического правдоподобия и возвращает его как второй выходной аргумент.

Если lmbda если не None, выполнить преобразование для этого значения.

alphafloat, опционально

Если lmbda равно None и alpha не None (по умолчанию), вернуть 100 * (1-alpha)% доверительный интервал для lmbda как третий выходной аргумент. Должно быть между 0.0 и 1.0.

Если lmbda не является None, alpha игнорируется.

оптимизаторвызываемый объект, необязательный

Если lmbda равно None, оптимизатор это скалярный оптимизатор, используемый для нахождения значения lmbda который минимизирует функцию отрицательного логарифма правдоподобия. оптимизатор является вызываемым объектом, принимающим один аргумент:

funcallable: Целевая функция, которая вычисляет отрицательную функцию логарифмического правдоподобия при заданном значении lmbda

и возвращает объект, например экземпляр scipy.optimize.OptimizeResult, которая содержит оптимальное значение lmbda в атрибуте x.

См. пример в boxcox_normmax или документацию scipy.optimize.minimize_scalar для получения дополнительной информации.

Если lmbda не является None, оптимизатор игнорируется.

Возвращает:

boxcoxndarray: Массив, преобразованный по степенному закону Бокса-Кокса.
maxlogfloat, опционально: Если lmbda параметр равен None, второй возвращаемый аргумент — это lmbda которая максимизирует функцию логарифма правдоподобия.
(min_ci, max_ci)кортеж из float, опционально: Если lmbda параметр равен None и alpha не является None, этот возвращаемый кортеж чисел с плавающей запятой представляет минимальный и максимальный доверительные пределы, учитывая alpha.

Смотрите также

probplot, boxcox_normplot, boxcox_normmax, boxcox_llf

Примечания

Преобразование Бокса-Кокса задается формулой:

\[y = \begin{cases} \frac{x^\lambda - 1}{\lambda}, &\text{for } \lambda \neq 0 \log(x), &\text{for } \lambda = 0 \end{cases}\]

boxcox требует, чтобы входные данные были положительными. Иногда преобразование Бокса-Кокса предоставляет параметр сдвига для достижения этого; boxcox не выполняется. Такой параметр сдвига эквивалентен добавлению положительной константы к x перед вызовом boxcox.

Доверительные границы, возвращаемые когда alpha предоставлен, даёт интервал где:

\[l(\hat{\lambda}) - l(\lambda) < \frac{1}{2}\chi^2(1 - \alpha, 1),\]

с \(l\) функция логарифма правдоподобия и \(\chi^2\) функция хи-квадрат.

Ссылки

G.E.P. Box и D.R. Cox, «An Analysis of Transformations», Journal of the Royal Statistical Society B, 26, 211-252 (1964).

Примеры

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

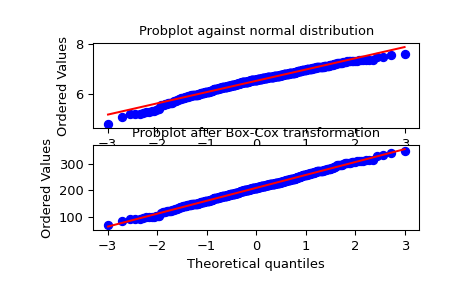
Мы генерируем некоторые случайные величины из ненормального распределения и строим вероятностный график для него, чтобы показать его ненормальность в хвостах:

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

Теперь мы используем boxcox для преобразования данных, чтобы они были ближе к нормальному распределению:

>>> ax2 = fig.add_subplot(212)
>>> xt, _ = stats.boxcox(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Box-Cox transformation')

>>> plt.show()