scipy.stats.

boxcox_llf

scipy.stats.boxcox_llf(lmb, данные, *, ось=0, keepdims=False, nan_policy='propagate')

Функция правдоподобия для преобразования Бокса-Кокса.

Параметры:

lmbскаляр

Параметр для преобразования Бокса-Кокса. См. boxcox подробности.

данныеarray_like

Данные для вычисления логарифмического правдоподобия Бокса-Кокса. Если данные является многомерным, логарифмическое правдоподобие вычисляется вдоль первой оси.

осьint, по умолчанию: 0

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

nan_policy{'propagate', 'omit', 'raise'

Определяет, как обрабатывать входные значения NaN.

• propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.

• omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.

• raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

llffloat или ndarray

Логарифмическое правдоподобие Бокса-Кокса для данные задан lmb. float для 1-D данные, массив в противном случае.

Смотрите также

boxcox, probplot, boxcox_normplot, boxcox_normmax

Примечания

Функция правдоподобия Box-Cox \(l\) определяется здесь как

\[l = (\lambda - 1) \sum_i^N \log(x_i) - \frac{N}{2} \log\left(\sum_i^N (y_i - \bar{y})^2 / N\right),\]

где \(N\) это количество точек данных data и \(y\) является преобразованными по Боксу-Коксу входными данными. Это соответствует профиль логарифмического правдоподобия исходных данных \(x\) с некоторыми опущенными постоянными членами.

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes

Сгенерируйте несколько случайных величин и вычислите значения правдоподобия Бокса-Кокса для них в диапазоне lmbda значения:

>>> rng = np.random.default_rng()
>>> x = stats.loggamma.rvs(5, loc=10, size=1000, random_state=rng)
>>> lmbdas = np.linspace(-2, 10)
>>> llf = np.zeros(lmbdas.shape, dtype=float)
>>> for ii, lmbda in enumerate(lmbdas):
...     llf[ii] = stats.boxcox_llf(lmbda, x)

Также найдите оптимальное значение lmbda с помощью boxcox:

>>> x_most_normal, lmbda_optimal = stats.boxcox(x)

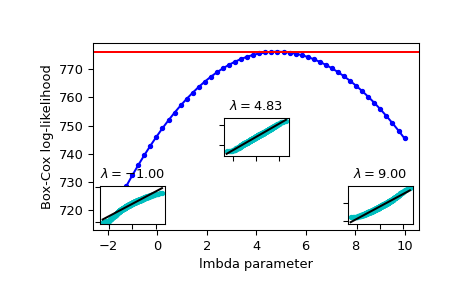
Построить лог-правдоподобие как функцию lmbda. Добавить оптимальную lmbda как горизонтальную линию для проверки, что это действительно оптимум:

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(lmbdas, llf, 'b.-')
>>> ax.axhline(stats.boxcox_llf(lmbda_optimal, x), color='r')
>>> ax.set_xlabel('lmbda parameter')
>>> ax.set_ylabel('Box-Cox log-likelihood')

Теперь добавьте несколько графиков вероятности, чтобы показать, что там, где логарифмическое правдоподобие максимизировано, данные, преобразованные с boxcox наиболее близко к нормальному:

>>> locs = [3, 10, 4]  # 'lower left', 'center', 'lower right'
>>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs):
...     xt = stats.boxcox(x, lmbda=lmbda)
...     (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt)
...     ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc)
...     ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-')
...     ax_inset.set_xticklabels([])
...     ax_inset.set_yticklabels([])
...     ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)

>>> plt.show()

НазадОткрыть во вкладке