scipy.stats.

yeojohnson

scipy.stats.yeojohnson(x, lmbda=None)

Возвращает набор данных, преобразованный с помощью преобразования Йео-Джонсона.

Параметры:

xndarray

Входной массив. Должен быть одномерным.

lmbdafloat, опционально

Если lmbda является None, найти лямбда, которая максимизирует функцию правдоподобия, и вернуть её как второй выходной аргумент. В противном случае преобразование выполняется для заданного значения.

Возвращает:

yeojohnson: ndarray

Массив, преобразованный по мощности Йео-Джонсона.

maxlogfloat, опционально

Если lmbda если параметр None, второй возвращаемый аргумент — это лямбда, максимизирующая функцию логарифмического правдоподобия.

Смотрите также

probplot, yeojohnson_normplot, yeojohnson_normmax, yeojohnson_llf, boxcox

Примечания

Преобразование Йео-Джонсона задается формулой:

\[\begin{split}y = \begin{cases} \frac{(x + 1)^\lambda - 1}{\lambda}, &\text{for } x \geq 0, \lambda \neq 0 \\ \log(x + 1), &\text{for } x \geq 0, \lambda = 0 \\ -\frac{(-x + 1)^{2 - \lambda} - 1}{2 - \lambda}, &\text{for } x < 0, \lambda \neq 2 \\ -\log(-x + 1), &\text{for } x < 0, \lambda = 2 \end{cases}\end{split}\]

В отличие от boxcox, yeojohnson не требует, чтобы входные данные были положительными.

Добавлено в версии 1.2.0.

Ссылки

I. Yeo и R.A. Johnson, “A New Family of Power Transformations to Improve Normality or Symmetry”, Biometrika 87.4 (2000):

Примеры

Попробуйте в вашем браузере!

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

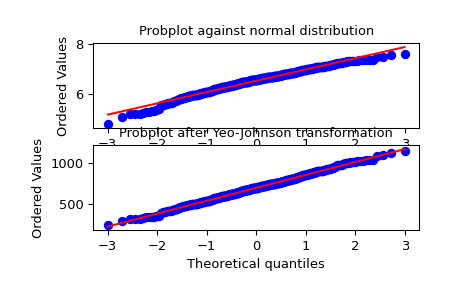
Мы генерируем некоторые случайные величины из ненормального распределения и строим вероятностный график для него, чтобы показать его ненормальность в хвостах:

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

Теперь мы используем yeojohnson для преобразования данных, чтобы они были ближе к нормальному распределению:

>>> ax2 = fig.add_subplot(212)
>>> xt, lmbda = stats.yeojohnson(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Yeo-Johnson transformation')

>>> plt.show()

НазадОткрыть во вкладке