scipy.stats.

goodness_of_fit

scipy.stats.goodness_of_fit(dist, данные, *, known_params=None, fit_params=None, guessed_params=None, статистика='ad', n_mc_samples=9999, rng=None, random_state=None)

Выполнить тест согласия, сравнивая данные с семейством распределений.

Для заданного семейства распределений и данных выполнить проверку нулевой гипотезы о том, что данные были взяты из распределения этого семейства. Любые известные параметры распределения могут быть указаны. Оставшиеся параметры распределения будут подогнаны под данные, и p-значение теста вычисляется соответственно. Доступно несколько статистик для сравнения распределения с данными.

Параметры:

distscipy.stats.rv_continuous

Объект, представляющий семейство распределений при нулевой гипотезе.

данные1D array_like

Конечные, нецензурированные данные для тестирования.

known_paramsdict, optional

Словарь, содержащий пары имя-значение известных параметров распределения. Монте-Карло выборки случайным образом извлекаются из нуль-гипотезного распределения с этими значениями параметров. Перед вычислением статистики для наблюдаемых данные и для каждого выборочного значения Монте-Карло подгоняются только оставшиеся неизвестные параметры семейства распределений нулевой гипотезы; известные параметры остаются фиксированными. Если все параметры семейства распределений известны, то шаг подгонки семейства распределений к каждому выбору опускается.

fit_paramsdict, optional

Словарь, содержащий пары имя-значение параметров распределения, которые уже были подогнаны к данным, например, с использованием scipy.stats.fit или fit метод dist. Монте-Карло выборки берутся из нуль-гипотезного распределения с указанными значениями параметра. Однако эти и все другие неизвестные параметры семейства нуль-гипотезного распределения всегда подгоняются к выборке, будь то наблюдаемая данные или выборка Монте-Карло, до вычисления статистики.

guessed_paramsdict, optional

Словарь, содержащий пары имя-значение параметров распределения, которые были угаданы. Эти параметры всегда считаются свободными параметрами и подгоняются как к предоставленным данные а также к выборкам Монте-Карло, взятым из распределения нулевой гипотезы. Цель этих guessed_params должны использоваться в качестве начальных значений для процедуры численной подгонки.

статистика{“ad”, “ks”, “cvm”, “filliben”} или вызываемый объект, опционально

Статистика, используемая для сравнения данных с распределением после подгонки неизвестных параметров семейства распределений к данным. Андерсон-Дарлинг ("ad") [1], Колмогорова-Смирнова («ks») [1], Крамера-фон Мизеса («cvm») [1], и Filliben (“filliben”) [7] статистики доступны. Альтернативно, вызываемый объект с сигнатурой (dist, data, axis) может быть предоставлен для вычисления статистики. Здесь dist является замороженным объектом распределения (возможно, с параметрами массива), data является массивом выборок Монте-Карло (совместимой формы), и axis является осью data по которому должна вычисляться статистика.

n_mc_samplesint, по умолчанию: 9999

Количество выборок Монте-Карло, извлеченных из нулевой гипотетической распределения для формирования нулевого распределения статистики. Размер каждой выборки такой же, как у заданной данные.

rng{None, int, numpy.random.Generator, опционально

Если rng передается по ключевому слову, типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator. Если rng уже является Generator экземпляр, то предоставленный экземпляр используется. Укажите rng для повторяемого поведения функции.

Если этот аргумент передаётся по позиции или random_state передается по ключевому слову, устаревшее поведение для аргумента random_state применяется:

• Если random_state равно None (или numpy.random), numpy.random.RandomState используется синглтон.

• Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state.

• Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator, этот ключевое слово было изменено с random_state to rng. В переходный период оба ключевых слова будут продолжать работать, хотя только одно может быть указано за раз. После переходного периода вызовы функций, использующие random_state ключевое слово будет выдавать предупреждения. Поведение обоих random_state и rng описаны выше, но только rng ключевое слово должно использоваться в новом коде.

Возвращает:

resGoodnessOfFitResult

Объект со следующими атрибутами.

fit_resultFitResult

Объект, представляющий соответствие предоставленным dist to данные. Этот объект включает значения параметров семейства распределений, которые полностью определяют нуль-гипотезное распределение, то есть распределение, из которого берутся Монте-Карло выборки.

статистикаfloat

Значение статистики, сравнивающей предоставленные данные к распределению нулевой гипотезы.

p-значениеfloat

Доля элементов в нулевом распределении со статистическими значениями, по крайней мере, такими же экстремальными, как статистическое значение предоставленного данные.

null_distributionndarray

Значение статистики для каждой выборки Монте-Карло, взятой из распределения нулевой гипотезы.

Примечания

Это обобщенная процедура проверки согласия Монте-Карло, частные случаи которой соответствуют различным тестам Андерсона-Дарлинга, тесту Лилиефорса, и т.д. Тест описан в [2], [3], и [4] как параметрический бутстрап-тест. Это тест Монте-Карло, в котором параметры, определяющие распределение, из которого берутся выборки, были оценены по данным. Мы описываем тест, используя «Монте-Карло», а не «параметрический бутстрап», чтобы избежать путаницы с более знакомым непараметрическим бутстрапом, и описываем, как проводится тест ниже.

Традиционные тесты согласия

Традиционно критические значения, соответствующие фиксированному набору уровней значимости, предварительно вычисляются с использованием методов Монте-Карло. Пользователи выполняют тест, вычисляя значение тестовой статистики только для их наблюдаемых данные и сравнение этого значения с табличными критическими значениями. Эта практика не очень гибкая, так как таблицы недоступны для всех распределений и комбинаций известных и неизвестных значений параметров. Кроме того, результаты могут быть неточными, когда критические значения интерполируются из ограниченных табличных данных, чтобы соответствовать размеру выборки пользователя и подобранным значениям параметров. Чтобы преодолеть эти недостатки, эта функция позволяет пользователю выполнять испытания Монте-Карло, адаптированные к их конкретным данным.

Алгоритмический обзор

Вкратце, эта процедура выполняет следующие шаги:

1. Подобрать неизвестные параметры к заданным данные, тем самым формируя распределение "нулевой гипотезы", и вычисляя статистику для этой пары данных и распределения.

2. Извлечь случайные выборки из этого распределения нулевой гипотезы.

3. Подогнать неизвестные параметры к каждой случайной выборке.

4. Вычислить статистику между каждой выборкой и распределением, которое было подогнано к выборке.

5. Сравните значение статистики, соответствующее данные из (1) против значений статистики, соответствующих случайным выборкам из (4). P-значение — это доля выборок со значением статистики, большим или равным статистике наблюдаемых данных.

Более подробно, шаги следующие.

Во-первых, любые неизвестные параметры семейства распределений, заданного dist подгоняются к предоставленным данные используя метод максимального правдоподобия. (Одно исключение — нормальное распределение с неизвестным положением и масштабом: мы используем скорректированное на смещение стандартное отклонение np.std(data, ddof=1) для масштаба, как рекомендуется в [1].) Эти значения параметров определяют конкретный член семейства распределений, называемого «нуль-гипотетическим распределением», то есть распределением, из которого были взяты данные при нулевой гипотезе. статистика, который сравнивает данные с распределением, вычисляется между данные и нуль-гипотетическое распределение.

Далее, многие (в частности n_mc_samples) новых образцов, каждый содержит то же количество наблюдений, что и данные, взяты из распределения нулевой гипотезы. Все неизвестные параметры семейства распределений dist обучены на каждая повторная выборкадолжны быть включены в старые категории. Значения, которые были в удаленных категориях, будут установлены в NaN статистика вычисляется между каждой выборкой и её соответствующим подобранным распределением. Эти значения статистики формируют нулевое распределение Монте-Карло (не путать с «нуль-гипотезным распределением» выше).

p-значение теста — это доля значений статистики в Монте-Карло нулевом распределении, которые по крайней мере так же экстремальны, как значение статистики предоставленного данные. Более точно, p-значение задаётся как

\[p = \frac{b + 1} {m + 1}\]

где \(b\) это количество статистических значений в Монте-Карло нулевом распределении, которые больше или равны статистическому значению, вычисленному для данные, и \(m\) это количество элементов в распределении нулевой гипотезы Монте-Карло (n_mc_samples). Добавление \(1\) к числителю и знаменателю можно рассматривать как включение значения статистики, соответствующего данные в нулевом распределении, но более формальное объяснение дано в [5].

Ограничения

Тест может быть очень медленным для некоторых семейств распределений, потому что неизвестные параметры семейства распределений должны быть подогнаны к каждому из Монте-Карло сэмплов, и для большинства распределений в SciPy подгонка распределения выполняется с помощью численной оптимизации.

Антипаттерн

По этой причине может возникнуть соблазн рассматривать параметры распределения, предварительно подобранные к данные (пользователем) как если бы они были known_params, как спецификация всех параметров распределения исключает необходимость подгонки распределения к каждому Монте-Карло образцу. (Это по сути то, как выполняется исходный тест Колмогорова-Смирнова.) Хотя такой тест может предоставить доказательства против нулевой гипотезы, тест консервативен в том смысле, что маленькие p-значения будут стремиться (сильно) переоценивать вероятность совершения ошибки I рода (то есть отклонения нулевой гипотезы, хотя она верна), и мощность теста низкая (то есть менее вероятно отклонение нулевой гипотезы даже когда нулевая гипотеза ложна). Это происходит потому, что выборки Монте-Карло менее вероятно согласуются с распределением, предполагаемым нулевой гипотезой, а также данные. Это обычно увеличивает значения статистики, записанные в нулевом распределении, так что большее их количество превышает значение статистики для данные, тем самым завышая p-значение.

Ссылки

[1] (1,2,3,4,5)

M. A. Stephens (1974). «EDF Statistics for Goodness of Fit and Some Comparisons.» Journal of the American Statistical Association, Vol. 69, pp. 730-737.

[2]

W. Stute, W. G. Manteiga, and M. P. Quindimil (1993). “Bootstrap based goodness-of-fit-tests.” Metrika 40.1: 243-256.

[3]

C. Genest, & B Rémillard. (2008). “Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models.” Annales de l’IHP Probabilités et statistiques. Vol. 44. No. 6.

[4]

I. Kojadinovic и J. Yan (2012). «Goodness-of-fit testing based on a weighted bootstrap: A fast large-sample alternative to the parametric bootstrap.» Canadian Journal of Statistics 40.3: 480-500.

[5]

B. Phipson и G. K. Smyth (2010). «P-значения перестановок никогда не должны быть нулевыми: вычисление точных P-значений при случайной выборке перестановок». Statistical Applications in Genetics and Molecular Biology 9.1.

[6]

H. W. Lilliefors (1967). “On the Kolmogorov-Smirnov test for normality with mean and variance unknown.” Journal of the American statistical Association 62.318: 399-402.

[7]

Filliben, James J. “The probability plot correlation coefficient test for normality.” Technometrics 17.1 (1975): 111-117.

Примеры

Попробуйте в вашем браузере!

Известный тест нулевой гипотезы о том, что данные были взяты из заданного распределения — это тест Колмогорова-Смирнова (KS), доступный в SciPy как scipy.stats.ks_1samp. Предположим, мы хотим проверить, соответствуют ли следующие данные:

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>> x = stats.uniform.rvs(size=75, random_state=rng)

были взяты из нормального распределения. Для выполнения KS-теста эмпирическая функция распределения наблюдаемых данных будет сравниваться с (теоретической) кумулятивной функцией распределения нормального распределения. Конечно, для этого нормальное распределение при нулевой гипотезе должно быть полностью определено. Обычно это делается сначала подгонкой loc и scale параметры распределения к наблюдаемым данным, затем выполнить тест.

>>> loc, scale = np.mean(x), np.std(x, ddof=1)
>>> cdf = stats.norm(loc, scale).cdf
>>> stats.ks_1samp(x, cdf)
KstestResult(statistic=0.1119257570456813,
             pvalue=0.2827756409939257,
             statistic_location=0.7751845155861765,
             statistic_sign=-1)

Преимущество KS-теста в том, что p-значение - вероятность получения значения статистики теста при нулевой гипотезе, столь же экстремального, как значение, полученное из наблюдаемых данных - может быть вычислено точно и эффективно. goodness_of_fit может только приблизительно давать эти результаты.

>>> known_params = {'loc': loc, 'scale': scale}
>>> res = stats.goodness_of_fit(stats.norm, x, known_params=known_params,
...                             statistic='ks', rng=rng)
>>> res.statistic, res.pvalue
(0.1119257570456813, 0.2788)

Статистика совпадает точно, но p-значение оценивается путем формирования "Монте-Карло нулевого распределения", то есть путем явного взятия случайных выборок из scipy.stats.norm с предоставленными параметрами и вычислением статистики для каждого. Доля этих значений статистики, по крайней мере, столь же экстремальных, как res.statistic аппроксимирует точное p-значение рассчитанное с помощью scipy.stats.ks_1samp.

эксперимент с выбираемыми пользователем критериями сглаживания: добавление штрафа P-сплайнов для дополнения штрафа второй производной любой член семейства нормальных распределений, а не конкретно из нормального распределения с параметрами положения и масштаба, подогнанными к наблюдаемой выборке. В этом случае Лиллиефорс [6] утверждали, что критерий Колмогорова-Смирнова слишком консервативен (т.е. p-значение завышает фактическую вероятность отвержения истинной нулевой гипотезы) и поэтому обладает низкой мощностью — способностью отвергать нулевую гипотезу, когда нулевая гипотеза на самом деле ложна. Действительно, наше p-значение выше составляет примерно 0,28, что слишком велико, чтобы отвергнуть нулевую гипотезу на любом общепринятом уровне значимости.

Подумайте, почему это может быть. Обратите внимание, что в KS-тесте выше статистика всегда сравнивает данные с функцией распределения нормального распределения, подобранного к наблюдаемые данные. Это имеет тенденцию уменьшать значение статистики для наблюдаемых данных, но является "несправедливым" при вычислении статистики для других выборок, таких как те, которые мы случайным образом извлекаем для формирования распределения нулевой гипотезы Монте-Карло. Это легко исправить: всякий раз, когда мы вычисляем статистику KS выборки, мы используем CDF нормального распределения, подобранного к эта выборка. Нулевое распределение в этом случае не было рассчитано точно и обычно аппроксимируется с использованием методов Монте-Карло, как описано выше. Здесь goodness_of_fit превосходно.

>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ks',
...                             rng=rng)
>>> res.statistic, res.pvalue
(0.1119257570456813, 0.0196)

Действительно, это p-значение намного меньше и достаточно мало, чтобы (правильно) отклонить нулевую гипотезу на обычных уровнях значимости, включая 5% и 2,5%.

Однако статистика KS не очень чувствительна ко всем отклонениям от нормальности. Изначальное преимущество статистики KS заключалось в возможности теоретического вычисления нулевого распределения, но теперь можно использовать более чувствительную статистику — приводящую к большей мощности теста — поскольку мы можем вычислительно аппроксимировать нулевое распределение. Статистика Андерсона-Дарлинга [1] обычно более чувствителен, и критические значения этой статистики были табулированы для различных уровней значимости и размеров выборок с использованием методов Монте-Карло.

>>> res = stats.anderson(x, 'norm')
>>> print(res.statistic)
1.2139573337497467
>>> print(res.critical_values)
[0.549 0.625 0.75  0.875 1.041]
>>> print(res.significance_level)
[15.  10.   5.   2.5  1. ]

Здесь наблюдаемое значение статистики превышает критическое значение, соответствующее уровню значимости 1%. Это говорит нам, что p-значение наблюдаемых данных меньше 1%, но каково оно? Мы могли бы интерполировать из этих (уже интерполированных) значений, но goodness_of_fit может оценивать его напрямую.

>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ad',
...                             rng=rng)
>>> res.statistic, res.pvalue
(1.2139573337497467, 0.0034)

Дополнительным преимуществом является использование goodness_of_fit не ограничивается конкретным набором распределений или условиями, в которых параметры известны, а какие должны быть оценены по данным. Вместо этого, goodness_of_fit может относительно быстро оценивать p-значения для любого распределения с достаточно быстрой и надежной fit метод. Например, здесь мы выполняем тест на соответствие с использованием статистики Крамера-фон Мизеса против распределения Рэлея с известным местоположением и неизвестным масштабом.

>>> rng = np.random.default_rng()
>>> x = stats.chi(df=2.2, loc=0, scale=2).rvs(size=1000, random_state=rng)
>>> res = stats.goodness_of_fit(stats.rayleigh, x, statistic='cvm',
...                             known_params={'loc': 0}, rng=rng)

Это выполняется довольно быстро, но для проверки надёжности fit метода, мы должны проверить результат подгонки.

>>> res.fit_result  # location is as specified, and scale is reasonable
  params: FitParams(loc=0.0, scale=2.1026719844231243)
 success: True
 message: 'The fit was performed successfully.'
>>> import matplotlib.pyplot as plt  # matplotlib must be installed to plot
>>> res.fit_result.plot()
>>> plt.show()

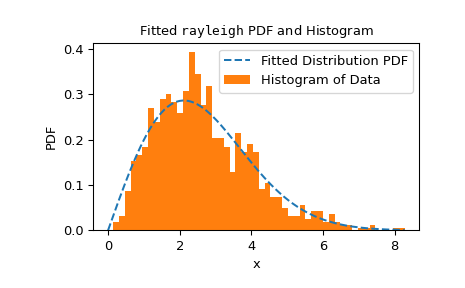
Если распределение не подогнано к наблюдаемым данным наилучшим образом, тест может не контролировать уровень ошибки первого рода, то есть вероятность отклонения нулевой гипотезы даже когда она верна.

Мы также должны искать экстремальные выбросы в нулевом распределении, которые могут быть вызваны ненадежной подгонкой. Они не обязательно делают результат недействительным, но имеют тенденцию снижать мощность теста.

>>> _, ax = plt.subplots()
>>> ax.hist(np.log10(res.null_distribution))
>>> ax.set_xlabel("log10 of CVM statistic under the null hypothesis")
>>> ax.set_ylabel("Frequency")
>>> ax.set_title("Histogram of the Monte Carlo null distribution")
>>> plt.show()

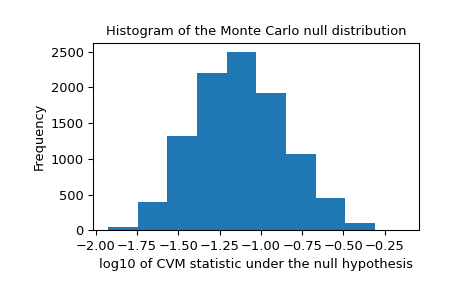
Этот график выглядит обнадёживающе.

Если fit метод работает надежно, и если распределение тестовой статистики не особенно чувствительно к значениям подобранных параметров, то p-значение, предоставленное goodness_of_fit ожидается, что будет хорошим приближением.

>>> res.statistic, res.pvalue
(0.2231991510248692, 0.0525)

НазадОткрыть во вкладке