scipy.stats.

siegelslopes#

scipy.stats.siegelslopes(y, x=None, метод='hierarchical', *, ось=None, nan_policy='propagate', keepdims=False)[источник]#

Вычисляет оценку Сигеля для набора точек (x, y).

siegelslopes реализует метод робастной линейной регрессии с использованием повторных медиан (см. [1]) для подгонки линии к точкам (x, y). Метод устойчив к выбросам с асимптотической точкой срыва 50%.

Параметры:

yarray_like

Зависимая переменная.

xarray_like или None, необязательный

Независимая переменная. Если None, используется arange(len(y)) вместо этого.

метод{‘hierarchical’, ‘separate’}

Если 'hierarchical', оценить пересечение с использованием оцененного наклона slope (опция по умолчанию). Если 'separate', оценить свободный член независимо от оцененного наклона. Подробности см. в примечаниях.

осьint или None, по умолчанию: None

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Определяет, как обрабатывать входные значения NaN.

propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.
omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.
raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

результатSiegelslopesResult экземпляр

Возвращаемое значение — объект со следующими атрибутами:

slopefloat: Оценка наклона линии регрессии.
interceptfloat: Оценка пересечения линии регрессии.

Смотрите также

theilslopes: аналогичная техника без повторных медиан

Примечания

С n = len(y), вычислить m_j как медиана наклонов от точки (x[j], y[j]) ко всем остальным n-1 точки. slope затем является медианой всех наклонов m_j. Даны два способа оценки пересечения в [1] который можно выбрать через параметр method. Иерархический подход использует оценённый наклон slope и вычисляет intercept как медиана y - slope*x. Другой подход оценивает точку пересечения отдельно следующим образом: для каждой точки (x[j], y[j]), вычисляет точки пересечения всех n-1 линии через оставшиеся точки и взять медиану i_j. intercept является медианой i_j.

Реализация вычисляет n раз медиана вектора размера n что может быть медленно для больших векторов. Существуют более эффективные алгоритмы (см. [2]), которые здесь не реализованы.

Для совместимости со старыми версиями SciPy возвращаемое значение ведёт себя как namedtuple длины 2, с полями slope и intercept, поэтому можно продолжать писать:

slope, intercept = siegelslopes(y, x)

Начиная с SciPy 1.9, np.matrix входные данные (не рекомендуется для нового кода) преобразуются в np.ndarray перед выполнением вычисления. В этом случае результатом будет скаляр или np.ndarray подходящей формы вместо 2D np.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр или np.ndarray вместо маскированного массива с mask=False.

Ссылки

[1] (1,2)

A. Siegel, "Robust Regression Using Repeated Medians", Biometrika, Vol. 69, pp. 242-244, 1982.

[2]

A. Stein and M. Werman, “Finding the repeated median regression line”, Proceedings of the Third Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 409-413, 1992.

Примеры

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

Вычислить наклон и пересечение. Для сравнения также вычислить наименьшие квадраты с linregress:

>>> res = stats.siegelslopes(y, x)
>>> lsq_res = stats.linregress(x, y)

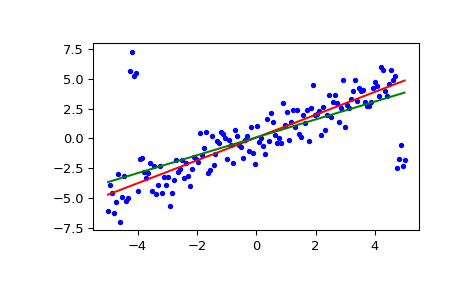
Построить результаты. Линия регрессии Сигеля показана красным. Зеленая линия показывает наименьшие квадраты для сравнения.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()

../../_images/scipy-stats-siegelslopes-1.png