theilslopes#
- scipy.stats.theilslopes(y, x=None, alpha=0.95, метод='separate', *, ось=None, nan_policy='propagate', keepdims=False)[источник]#
Вычисляет оценку Тейла-Сена для набора точек (x, y).
theilslopesреализует метод устойчивой линейной регрессии. Он вычисляет наклон как медиану всех наклонов между парными значениями.- Параметры:
- yarray_like
Зависимая переменная.
- xarray_like или None, необязательный
Независимая переменная. Если None, используется
arange(len(y))вместо этого.- alphafloat, опционально
Степень доверия между 0 и 1. По умолчанию — 95% доверительный интервал. Обратите внимание, что
alphaсимметричен относительно 0.5, т.е. и 0.1, и 0.9 интерпретируются как «найти 90% доверительный интервал».- метод{'joint', 'separate'}, опционально
Метод, используемый для вычисления оценки для пересечения. Поддерживаются следующие методы,
‘joint’: Использует np.median(y - slope * x) в качестве пересечения.
- ‘separate’: Использует np.median(y) - slope * np.median(x)
как intercept.
По умолчанию 'separate'.
Добавлено в версии 1.8.0.
- осьint или None, по умолчанию: None
Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если
None, вход будет сведён в одномерный массив перед вычислением статистики.- nan_policy{‘propagate’, ‘omit’, ‘raise’}
Определяет, как обрабатывать входные значения NaN.
propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.raise: если присутствует NaN, тоValueErrorбудет вызвано исключение.
- keepdimsbool, по умолчанию: False
Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.
- Возвращает:
- результат
TheilslopesResultэкземпляр Возвращаемое значение — объект со следующими атрибутами:
- slopefloat
Наклон Тейла.
- interceptfloat
Пересечение линии Тейла.
- низкий_наклонfloat
Нижняя граница доверительного интервала для slope.
- high_slopefloat
Верхняя граница доверительного интервала для slope.
- результат
Смотрите также
siegelslopesаналогичная техника с использованием повторяющихся медиан
Примечания
Реализация
theilslopesследует [1]. Свободный член не определён в [1], и здесь он определяется какmedian(y) - slope*median(x), который приведён в [3]. Другие определения перехвата существуют в литературе, такие какmedian(y - slope*x)в [4]. Подход к вычислению интерсепта может определяться параметромmethod. Доверительный интервал для пересечения не предоставляется, так как этот вопрос не рассматривается в [1].Для совместимости со старыми версиями SciPy возвращаемое значение ведёт себя как
namedtupleдлины 4, с полямиslope,intercept,low_slope, иhigh_slope, поэтому можно продолжать писать:slope, intercept, low_slope, high_slope = theilslopes(y, x)
Начиная с SciPy 1.9,
np.matrixвходные данные (не рекомендуется для нового кода) преобразуются вnp.ndarrayперед выполнением вычисления. В этом случае результатом будет скаляр илиnp.ndarrayподходящей формы вместо 2Dnp.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр илиnp.ndarrayвместо маскированного массива сmask=False.Ссылки
[1] (1,2,3)P.K. Sen, “Estimates of the regression coefficient based on Kendall’s tau”, J. Am. Stat. Assoc., Vol. 63, pp. 1379-1389, 1968.
[2]Х. Тейл, «Рангово-инвариантный метод линейного и полиномиального регрессионного анализа I, II и III», Nederl. Akad. Wetensch., Proc. 53:, стр. 386-392, стр. 521-525, стр. 1397-1412, 1950.
[3]W.L. Conover, «Практическая непараметрическая статистика», 2-е изд., John Wiley and Sons, Нью-Йорк, стр. 493.
Примеры
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt
>>> x = np.linspace(-5, 5, num=150) >>> y = x + np.random.normal(size=x.size) >>> y[11:15] += 10 # add outliers >>> y[-5:] -= 7
Вычислить наклон, пересечение и 90% доверительный интервал. Для сравнения, также вычислить метод наименьших квадратов с
linregress:>>> res = stats.theilslopes(y, x, 0.90, method='separate') >>> lsq_res = stats.linregress(x, y)
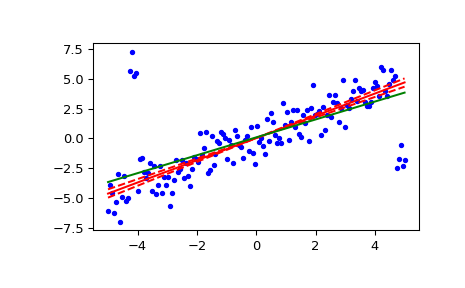
Постройте результаты. Линия регрессии Тейла-Сена показана красным, пунктирные красные линии иллюстрируют доверительный интервал наклона (обратите внимание, что пунктирные красные линии не являются доверительным интервалом регрессии, так как доверительный интервал пересечения не включён). Зелёная линия показывает наименьшие квадраты для сравнения.
>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> ax.plot(x, y, 'b.') >>> ax.plot(x, res[1] + res[0] * x, 'r-') >>> ax.plot(x, res[1] + res[2] * x, 'r--') >>> ax.plot(x, res[1] + res[3] * x, 'r--') >>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-') >>> plt.show()