Как создавать массивы с регулярно расположенными значениями#

Существует несколько функций NumPy, которые схожи по применению, но дают немного разные результаты, что может вызвать путаницу, если не уверены, когда и как их использовать. Следующее руководство призвано перечислить эти функции и описать их рекомендуемое использование.

Упомянутые здесь функции — это

1D области (интервалы)#

`linspace` vs. `arange`#

Оба numpy.linspace и numpy.arange предоставляет способы разделения интервала (одномерной области) на подынтервалы равной длины. Эти разделения будут варьироваться в зависимости от выбранных начальной и конечной точек, а также шаг (длина подынтервалов).

Используйте numpy.arange если требуются целочисленные шаги.

numpy.arange полагается на размер шага для определения количества элементов в возвращаемом массиве, который исключает конечную точку. Это определяется через step аргумент для arange.

Пример:
```
>>> np.arange(0, 10, 2)  # np.arange(start, stop, step)
array([0, 2, 4, 6, 8])
```
Аргументы start и stop должны быть целыми или вещественными числами, но не комплексными. numpy.arange похож на встроенный в Python range.

Неточности с плавающей запятой могут сделать arange результаты с числами с плавающей точкой запутанны. В этом случае следует использовать numpy.linspace вместо этого.
Используйте numpy.linspace если вы хотите, чтобы конечная точка была включена в результат, или если вы используете нецелый шаг.

numpy.linspace может включают конечную точку и определяют размер шага из число аргумент, который указывает количество элементов в возвращаемом массиве.

Включение конечной точки определяется необязательным булевым аргументом endpoint, который по умолчанию равен True. Обратите внимание, что выбор endpoint=False изменит вычисление размера шага и последующий вывод функции.

Пример:
```
>>> np.linspace(0.1, 0.2, num=5)  # np.linspace(start, stop, num)
array([0.1  , 0.125, 0.15 , 0.175, 0.2  ])
>>> np.linspace(0.1, 0.2, num=5, endpoint=False)
array([0.1, 0.12, 0.14, 0.16, 0.18])
```
numpy.linspace также может использоваться с комплексными аргументами:
```
>>> np.linspace(1+1.j, 4, 5, dtype=np.complex64)
array([1.  +1.j  , 1.75+0.75j, 2.5 +0.5j , 3.25+0.25j, 4.  +0.j  ],
      dtype=complex64)
```

Другие примеры#

Могут возникнуть неожиданные результаты, если используются значения с плавающей точкой как step в numpy.arange. Чтобы избежать этого, убедитесь, что все преобразования с плавающей точкой происходят после вычисления результатов. Например, замените
```
>>> list(np.arange(0.1,0.4,0.1).round(1))
[0.1, 0.2, 0.3, 0.4]  # endpoint should not be included!
```
с
```
>>> list(np.arange(1, 4, 1) / 10.0)
[0.1, 0.2, 0.3]  # expected result
```

Обратите внимание, что

>>> np.arange(0, 1.12, 0.04)
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04, 1.08, 1.12])

и

>>> np.arange(0, 1.08, 0.04)
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04])

Они различаются из-за числового шума. При использовании значений с плавающей точкой возможно, что 0 + 0.04 * 28 < 1.12, и так 1.12 находится в интервале. На самом деле, это именно так:

>>> 1.12/0.04
28.000000000000004

Но 0 + 0.04 * 27 >= 1.08 так что 1.08 исключается:

>>> 1.08/0.04
27.0

В качестве альтернативы вы можете использовать np.arange(0, 28)*0.04 который всегда даст вам точный контроль над конечной точкой, поскольку она является целочисленной:

>>> np.arange(0, 28)*0.04
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04, 1.08])

`geomspace` и `logspace`#

numpy.geomspace похож на numpy.linspace, но с числами, расположенными равномерно в логарифмическом масштабе (геометрическая прогрессия). Конечная точка включена в результат.

Пример:

>>> np.geomspace(2, 3, num=5)
array([2.        , 2.21336384, 2.44948974, 2.71080601, 3.        ])

numpy.logspace похож на numpy.geomspace, но с указанием начальной и конечной точек в виде логарифмов (с основанием 10 по умолчанию):

>>> np.logspace(2, 3, num=5)
array([ 100.        ,  177.827941  ,  316.22776602,  562.34132519, 1000.        ])

В линейном пространстве последовательность начинается с base ** start (base в степени start) и заканчивается base ** stop:

>>> np.logspace(2, 3, num=5, base=2)
array([4.        , 4.75682846, 5.65685425, 6.72717132, 8.        ])

N-мерные области#

N-мерные области могут быть разделены на grids. Это можно сделать с помощью одной из следующих функций.

`meshgrid`#

Цель numpy.meshgrid создаёт прямоугольную сетку из набора одномерных координатных массивов.

Заданные массивы:

>>> x = np.array([0, 1, 2, 3])
>>> y = np.array([0, 1, 2, 3, 4, 5])

meshgrid создаст два координатных массива, которые можно использовать для генерации пар координат, определяющих эту сетку:

>>> xx, yy = np.meshgrid(x, y)
>>> xx
array([[0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3]])
>>> yy
array([[0, 0, 0, 0],
       [1, 1, 1, 1],
       [2, 2, 2, 2],
       [3, 3, 3, 3],
       [4, 4, 4, 4],
       [5, 5, 5, 5]])

>>> import matplotlib.pyplot as plt
>>> plt.plot(xx, yy, marker='.', color='k', linestyle='none')

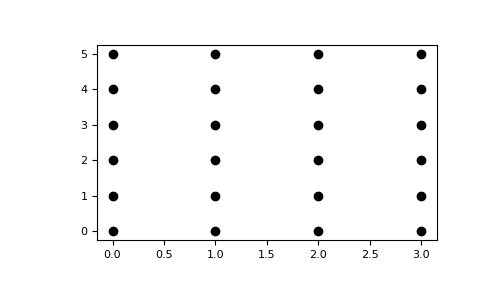
`mgrid`#

numpy.mgrid может использоваться как ярлык для создания сеток. Это не функция, но при индексировании возвращает многомерную сетку.

>>> xx, yy = np.meshgrid(np.array([0, 1, 2, 3]), np.array([0, 1, 2, 3, 4, 5]))
>>> xx.T, yy.T
(array([[0, 0, 0, 0, 0, 0],
        [1, 1, 1, 1, 1, 1],
        [2, 2, 2, 2, 2, 2],
        [3, 3, 3, 3, 3, 3]]),
 array([[0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5]]))

>>> np.mgrid[0:4, 0:6]
array([[[0, 0, 0, 0, 0, 0],
        [1, 1, 1, 1, 1, 1],
        [2, 2, 2, 2, 2, 2],
        [3, 3, 3, 3, 3, 3]],

       [[0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5]]])

`ogrid`#

Аналогично numpy.mgrid, numpy.ogrid возвращает открыть многомерная сетка. Это означает, что при индексации только одно измерение каждого возвращаемого массива больше 1. Это позволяет избежать повторения данных и таким образом экономит память, что часто желательно.

Эти разреженные координатные сетки предназначены для использования с Трансляция (Broadcasting). Когда все координаты используются в выражении, трансляция всё равно приводит к полностью размерному результирующему массиву.

>>> np.ogrid[0:4, 0:6]
(array([[0],
        [1],
        [2],
        [3]]), array([[0, 1, 2, 3, 4, 5]]))

Все три описанных здесь метода могут использоваться для вычисления значений функции на сетке.

>>> g = np.ogrid[0:4, 0:6]
>>> zg = np.sqrt(g[0]**2 + g[1]**2)
>>> g[0].shape, g[1].shape, zg.shape
((4, 1), (1, 6), (4, 6))
>>> m = np.mgrid[0:4, 0:6]
>>> zm = np.sqrt(m[0]**2 + m[1]**2)
>>> np.array_equal(zm, zg)
True

Как создавать массивы с регулярно расположенными значениями#

1D области (интервалы)#

linspace vs. arange#

Другие примеры#

geomspace и logspace#

N-мерные области#

meshgrid#

mgrid#

ogrid#

`linspace` vs. `arange`#

`geomspace` и `logspace`#

`meshgrid`#

`mgrid`#

`ogrid`#