numpy.meshgrid

numpy.meshgrid(*xi, copy=True, разреженный=False, индексирование='xy')

Верните кортеж координатных матриц из координатных векторов.

Создать N-мерные координатные массивы для векторизованных вычислений N-мерных скалярных/векторных полей на N-мерных сетках, заданных одномерными координатными массивами x1, x2,…, xn.

Параметры:

x1, x2,…, xnarray_like

Одномерные массивы, представляющие координаты сетки.

индексирование{‘xy’, ‘ij’}, опционально

Декартова (‘xy’, по умолчанию) или матричная (‘ij’) индексация вывода. См. примечания для подробностей.

разреженныйbool, необязательно

Если True, форма возвращаемого координатного массива для измерения i уменьшается с (N1, ..., Ni, ... Nn) to (1, ..., 1, Ni, 1, ..., 1). Эти разреженные координатные сетки предназначены для использования с Трансляция (Broadcasting). Когда все координаты используются в выражении, трансляция все равно приводит к полностью размерному результирующему массиву.

По умолчанию False.

copybool, необязательно

Если False, возвращается представление исходных массивов для экономии памяти. По умолчанию True. Обратите внимание, что sparse=False, copy=False вероятно, вернёт несмежные массивы. Более того, более одного элемента широковещательного массива могут ссылаться на одно место в памяти. Если вам нужно записывать в массивы, сначала создайте копии.

Возвращает:

X1, X2,…, XNкортеж ndarrays

Для векторов x1, x2,…, xn с длинами Ni=len(xi)возвращает (N1, N2, N3,..., Nn) массивы формы, если indexing='ij' или (N2, N1, N3,..., Nn) массивов формы, если indexing='xy' с элементами xi повторяется для заполнения матрицы по первой размерности x1, второй для x2 и так далее.

Смотрите также

mgrid

Построить многомерную «сетку» с использованием нотации индексации.

ogrid

Построение открытой многомерной "сетки" с использованием индексной нотации.

Как индексировать ndarrays

Примечания

Эта функция поддерживает обе соглашения об индексации через аргумент ключевого слова indexing. Передача строки 'ij' возвращает сетку с матричной индексацией, а 'xy' возвращает сетку с декартовой индексацией. В 2-D случае с входами длины M и N выходы имеют форму (N, M) для индексации 'xy' и (M, N) для индексации 'ij'. В 3-D случае с входами длины M, N и P выходы имеют форму (N, M, P) для индексации 'xy' и (M, N, P) для индексации 'ij'. Разница иллюстрируется следующим фрагментом кода:

xv, yv = np.meshgrid(x, y, indexing='ij')
for i in range(nx):
    for j in range(ny):
        # treat xv[i,j], yv[i,j]

xv, yv = np.meshgrid(x, y, indexing='xy')
for i in range(nx):
    for j in range(ny):
        # treat xv[j,i], yv[j,i]

В случае 1-D и 0-D индексация и ключевые слова sparse не имеют эффекта.

Примеры

Попробуйте в вашем браузере!

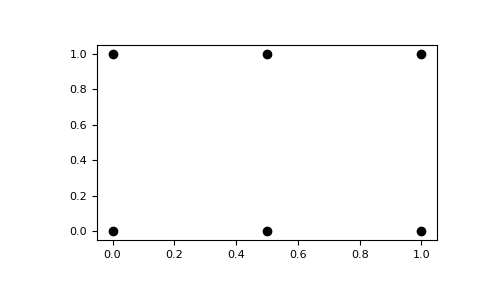
>>> import numpy as np
>>> nx, ny = (3, 2)
>>> x = np.linspace(0, 1, nx)
>>> y = np.linspace(0, 1, ny)
>>> xv, yv = np.meshgrid(x, y)
>>> xv
array([[0. , 0.5, 1. ],
       [0. , 0.5, 1. ]])
>>> yv
array([[0.,  0.,  0.],
       [1.,  1.,  1.]])

Результат meshgrid является координатной сеткой:

>>> import matplotlib.pyplot as plt
>>> plt.plot(xv, yv, marker='o', color='k', linestyle='none')
>>> plt.show()

Вы можете создавать разреженные выходные массивы для экономии памяти и времени вычислений.

>>> xv, yv = np.meshgrid(x, y, sparse=True)
>>> xv
array([[0. ,  0.5,  1. ]])
>>> yv
array([[0.],
       [1.]])

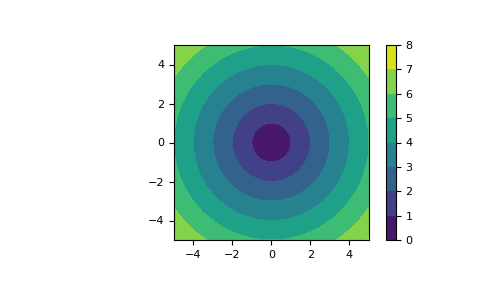
meshgrid очень полезно для вычисления функций на сетке. Если функция зависит от всех координат, можно использовать как плотные, так и разреженные выходные данные.

>>> x = np.linspace(-5, 5, 101)
>>> y = np.linspace(-5, 5, 101)
>>> # full coordinate arrays
>>> xx, yy = np.meshgrid(x, y)
>>> zz = np.sqrt(xx**2 + yy**2)
>>> xx.shape, yy.shape, zz.shape
((101, 101), (101, 101), (101, 101))
>>> # sparse coordinate arrays
>>> xs, ys = np.meshgrid(x, y, sparse=True)
>>> zs = np.sqrt(xs**2 + ys**2)
>>> xs.shape, ys.shape, zs.shape
((1, 101), (101, 1), (101, 101))
>>> np.array_equal(zz, zs)
True

>>> h = plt.contourf(x, y, zs)
>>> plt.axis('scaled')
>>> plt.colorbar()
>>> plt.show()

НазадОткрыть во вкладке