Многомерная интерполяция данных на регулярной сетке (RegularGridInterpolator)

Предположим, у вас есть N-мерные данные на регулярной сетке, и вы хотите их интерполировать. В таком случае, RegularGridInterpolator может быть полезным. Поддерживается несколько стратегий интерполяции: ближайший сосед, линейная и сплайны тензорного произведения нечетной степени.

Строго говоря, этот класс эффективно обрабатывает данные, заданные на прямолинейный сетки: гиперкубические решётки с возможным неравномерным шагом между точками. Количество точек на измерение может различаться для разных измерений.

Следующий пример демонстрирует его использование и сравнивает результаты интерполяции с использованием каждого метода.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import RegularGridInterpolator

Предположим, мы хотим интерполировать эту 2-D функцию.

>>> def F(u, v):
...     return u * np.cos(u * v) + v * np.sin(u * v)

Предположим, мы знаем только некоторые данные на регулярной сетке.

>>> fit_points = [np.linspace(0, 3, 8), np.linspace(0, 3, 11)]
>>> values = F(*np.meshgrid(*fit_points, indexing='ij'))

Создание тестовых точек и истинных значений для вычислений.

>>> ut, vt = np.meshgrid(np.linspace(0, 3, 80), np.linspace(0, 3, 80), indexing='ij')
>>> true_values = F(ut, vt)
>>> test_points = np.array([ut.ravel(), vt.ravel()]).T

Мы можем создать интерполятор и интерполировать тестовые точки, используя каждый метод.

>>> interp = RegularGridInterpolator(fit_points, values)
>>> fig, axes = plt.subplots(2, 3, figsize=(10, 6))
>>> axes = axes.ravel()
>>> fig_index = 0
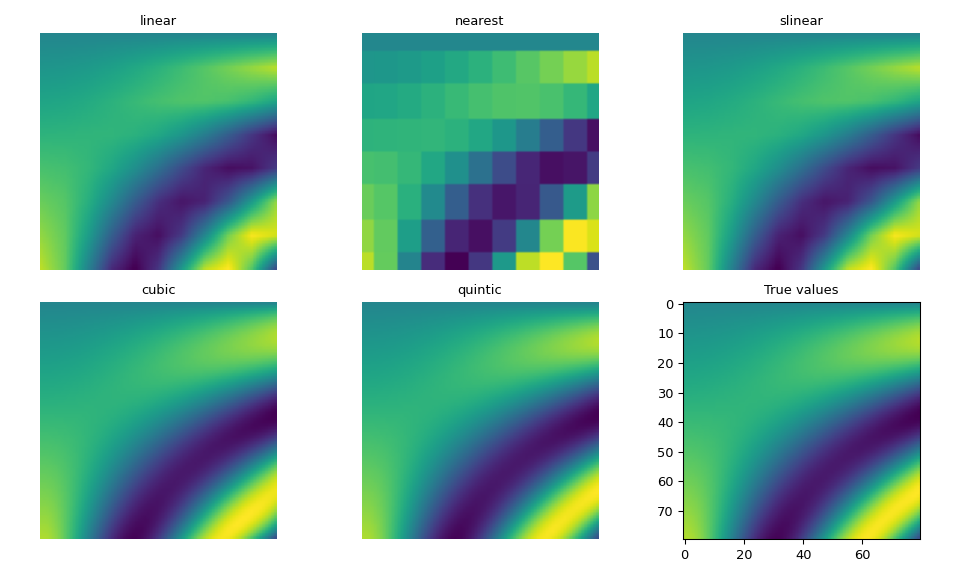
>>> for method in ['linear', 'nearest', 'slinear', 'cubic', 'quintic']:
...     im = interp(test_points, method=method).reshape(80, 80)
...     axes[fig_index].imshow(im)
...     axes[fig_index].set_title(method)
...     axes[fig_index].axis("off")
...     fig_index += 1
>>> axes[fig_index].imshow(true_values)
>>> axes[fig_index].set_title("True values")
>>> fig.tight_layout()
>>> fig.show()

Как и ожидалось, интерполяции сплайнами более высокой степени ближе всего к истинным значениям, хотя их вычисление дороже, чем с линейный или ближайший. slinear интерполяция также соответствует линейный интерполяция.

Если ваши данные таковы, что методы сплайнов вызывают звон, вы можете рассмотреть использование method="pchip", который использует тензорное произведение интерполяторов PCHIP, а PchipInterpolator на измерение.

Если вы предпочитаете функциональный интерфейс вместо явного создания экземпляра класса, используйте interpn удобная функция предоставляет эквивалентную функциональность.

В частности, эти две формы дают идентичные результаты:

>>> from scipy.interpolate import interpn
>>> rgi = RegularGridInterpolator(fit_points, values)
>>> result_rgi = rgi(test_points)

и

>>> result_interpn = interpn(fit_points, values, test_points)
>>> np.allclose(result_rgi, result_interpn, atol=1e-15)
True

Для данных, ограниченных (N-1)-мерным подпространством N-мерного пространства, т.е. когда одна из осей сетки имеет длину 1, экстраполяция вдоль этой оси контролируется параметром fill_value именованный параметр:

>>> x = np.array([0, 5, 10])
>>> y = np.array([0])
>>> data = np.array([[0], [5], [10]])
>>> rgi = RegularGridInterpolator((x, y), data,
...                               bounds_error=False, fill_value=None)
>>> rgi([(2, 0), (2, 1), (2, -1)])   # extrapolates the value on the axis
array([2., 2., 2.])
>>> rgi.fill_value = -101
>>> rgi([(2, 0), (2, 1), (2, -1)])
array([2., -101., -101.])

Примечание

Если входные данные таковы, что размерности входных данных имеют несопоставимые единицы измерения и различаются на много порядков величины, интерполянт может иметь числовые артефакты. Рассмотрите возможность масштабирования данных перед интерполяцией.

Пакетные размеры values

Предположим, у вас есть векторная функция \(f(x) = y\), где \(x\) и \(y\) являются векторами, возможно, разной длины, и вы хотите выполнить выборку функции на сетке \(x\) значения. Один из способов решения этой проблемы — использовать тот факт, что RegularGridInterpolator позволяет values с хвостовой измерения.

В соответствии с тем, как 1D интерполяторы интерпретируют многомерные массивы, интерпретация заключается в том, что первый \(N\) размерности values массивы являются размерностями данных (т.е. они соответствуют точкам, определенным grid аргумент), и хвостовой размерности являются осями пакетов. Обратите внимание, что это противоречит обычным соглашениям о трансляции NumPy, где трансляция происходит вдоль ведущий измерения.

Для иллюстрации:

>>> n = 5   # the number of batch components

>>> # make a 3D grid
>>> x1 = np.linspace(-np.pi, np.pi, 10)
>>> x2 = np.linspace(0.0, np.pi, 15)
>>> x3 = np.linspace(0.0, np.pi/2, 20)
>>> points = (x1, x2, x3)
>>>
>>> # define a function and sample it on the grid
>>> def f(x1, x2, x3, n):
...     lst = [np.sin(np.pi*x1/2) * np.exp(x2/2) + x3 + i for i in range(n)]
...     return np.asarray(lst)
>>>
>>> X1, X2, X3 = np.meshgrid(x1, x2, x3, indexing="ij")
>>> values = f(X1, X2, X3, n)
>>> values.shape
(5, 10, 15, 20)
>>>
>>> # prepare the data and construct the interpolator
>>> values = np.moveaxis(values, 0, -1)
>>> values.shape
(10, 15, 20, 5)     # the batch dimension is 5
>>> rgi = RegularGridInterpolator(points, values)
>>>
>>> # Coordinates to compute the interpolation at
>>> x = np.asarray([0.2, np.pi/2.1, np.pi/4.1])
>>>
# evaluate
>>> rgi(x).shape
(1, 5)

В этом примере мы оценили пакет \(n=5\) функциях на трехмерной сетке. В общем случае допускаются несколько размерностей пакетной обработки, и форма результата получается путем добавления формы пакетной обработки (в этом примере (5,)) к форме входных данных x (в этом примере, (1,)).

Равномерно распределённые данные

Если вы работаете с данными на декартовых сетках с целочисленными координатами, например, при передискретизации данных изображения, эти процедуры могут быть не оптимальным выбором. Рассмотрите использование scipy.ndimage.map_coordinates вместо этого.

Для данных с плавающей запятой на сетках с равным интервалом, map_coordinates может быть легко обернут в RegularGridInterpolator похожий. Ниже приведён простой пример, основанный на пакет 'regulargrid' Йоханнеса Бюхнера:

class CartesianGridInterpolator:
    def __init__(self, points, values, method='linear'):
        self.limits = np.array([[min(x), max(x)] for x in points])
        self.values = np.asarray(values, dtype=float)
        self.order = {'linear': 1, 'cubic': 3, 'quintic': 5}[method]

    def __call__(self, xi):
        """
        `xi` here is an array-like (an array or a list) of points.

        Each "point" is an ndim-dimensional array_like, representing
        the coordinates of a point in ndim-dimensional space.
        """
        # transpose the xi array into the ``map_coordinates`` convention
        # which takes coordinates of a point along columns of a 2D array.
        xi = np.asarray(xi).T

        # convert from data coordinates to pixel coordinates
        ns = self.values.shape
        coords = [(n-1)*(val - lo) / (hi - lo)
                  for val, n, (lo, hi) in zip(xi, ns, self.limits)]

        # interpolate
        return map_coordinates(self.values, coords,
                               order=self.order,
                               cval=np.nan)  # fill_value

Эта обёртка может использоваться как (почти) прямая замена для RegularGridInterpolator:

>>> x, y = np.arange(5), np.arange(6)
>>> xx, yy = np.meshgrid(x, y, indexing='ij')
>>> values = xx**3 + yy**3
>>> rgi = RegularGridInterpolator((x, y), values, method='linear')
>>> rgi([[1.5, 1.5], [3.5, 2.6]])
array([ 9. , 64.9])
>>> cgi = CartesianGridInterpolator((x, y), values, method='linear')
>>> cgi([[1.5, 1.5], [3.5, 2.6]])
array([ 9. , 64.9])

Обратите внимание, что приведенный выше пример использует map_coordinates граничные условия. Таким образом, результаты cubic и quintic интерполяции могут отличаться от таковых у RegularGridInterpolator. См. scipy.ndimage.map_coordinates документацию для получения дополнительных сведений о граничных условиях и других дополнительных аргументах. Наконец, отметим, что этот упрощённый пример предполагает, что входные данные представлены в порядке возрастания.