Оптимизация (scipy.optimize)

The scipy.optimize пакет предоставляет несколько часто используемых алгоритмов оптимизации. Подробный список доступен: scipy.optimize (также может быть найдено с помощью help(scipy.optimize)).

Локальная минимизация многомерных скалярных функций (minimize)

The minimize функция предоставляет общий интерфейс для алгоритмов безусловной и условной минимизации скалярных функций многих переменных в scipy.optimize. Чтобы продемонстрировать функцию минимизации, рассмотрим задачу минимизации функции Розенброка от \(N\) переменные:

\[f\left(\mathbf{x}\right)=\sum_{i=1}^{N-1}100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}.\]

Минимальное значение этой функции равно 0, которое достигается, когда \(x_{i}=1.\)

Обратите внимание, что функция Розенброка и её производные включены в scipy.optimize. Реализации, показанные в следующих разделах, предоставляют примеры того, как определить целевую функцию, а также её функции Якобиана и Гессиана. Целевые функции в scipy.optimize ожидают массив numpy в качестве первого параметра, который должен быть оптимизирован, и должны возвращать значение с плавающей точкой. Точная сигнатура вызова должна быть f(x, *args) где x представляет массив numpy и args кортеж дополнительных аргументов, передаваемых целевой функции.

Минимизация без ограничений

Алгоритм симплекса Нелдера-Мида (method='Nelder-Mead')

В примере ниже, minimize подпрограмма используется с Nelder-Mead симплекс-алгоритм (выбранный через method параметр):

>>> import numpy as np
>>> from scipy.optimize import minimize

>>> def rosen(x):
...     """The Rosenbrock function"""
...     return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)

>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(rosen, x0, method='nelder-mead',
...                options={'xatol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571

>>> print(res.x)
[1. 1. 1. 1. 1.]

Симплекс-алгоритм, вероятно, самый простой способ минимизации достаточно хорошо ведущей себя функции. Он требует только вычислений функции и является хорошим выбором для простых задач минимизации. Однако, поскольку он не использует никаких вычислений градиента, поиск минимума может занять больше времени.

Другой алгоритм оптимизации, которому для нахождения минимума нужны только вызовы функций, это Пауэллметод доступен при установке method='powell' в minimize.

Чтобы продемонстрировать, как передавать дополнительные аргументы в целевую функцию, минимизируем функцию Розенброка с дополнительным масштабирующим коэффициентом a и смещение b:

\[f\left(\mathbf{x}, a, b\right)=\sum_{i=1}^{N-1}a\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2} + b.\]

Снова используя minimize обычно это можно решить следующим блоком кода для примерных параметров a=0.5 и b=1.

>>> def rosen_with_args(x, a, b):
...     """The Rosenbrock function with additional arguments"""
...     return sum(a*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0) + b

>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(rosen_with_args, x0, method='nelder-mead',
...                args=(0.5, 1.), options={'xatol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 1.000000
         Iterations: 319 # may vary
         Function evaluations: 525 # may vary

>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

В качестве альтернативы использованию args параметр minimize, просто оберните целевую функцию в новую функцию, которая принимает только xЭтот подход также полезен, когда необходимо передать дополнительные параметры в целевую функцию в качестве аргументов ключевых слов.

>>> def rosen_with_args(x, a, *, b):  # b is a keyword-only argument
...     return sum(a*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0) + b
>>> def wrapped_rosen_without_args(x):
...     return rosen_with_args(x, 0.5, b=1.)  # pass in `a` and `b`
>>> x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
>>> res = minimize(wrapped_rosen_without_args, x0, method='nelder-mead',
...                options={'xatol': 1e-8,})
>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

Другой альтернативой является использование functools.partial.

>>> from functools import partial
>>> partial_rosen = partial(rosen_with_args, a=0.5, b=1.)
>>> res = minimize(partial_rosen, x0, method='nelder-mead',
...                options={'xatol': 1e-8,})
>>> print(res.x)
[1.         1.         1.         1.         0.99999999]

Алгоритм Бройдена-Флетчера-Голдфарба-Шанно (method='BFGS')

Для более быстрой сходимости к решению эта процедура использует градиент целевой функции. Если градиент не предоставлен пользователем, он оценивается с использованием первых разностей. Метод Бройдена-Флетчера-Гольдфарба-Шанно (BFGS) обычно требует меньше вызовов функции, чем симплекс-алгоритм, даже когда градиент должен быть оценен.

Для демонстрации этого алгоритма снова используется функция Розенброка. Градиент функции Розенброка — это вектор:

\begin{eqnarray*} \frac{\partial f}{\partial x_{j}} & = & \sum_{i=1}^{N}200\left(x_{i}-x_{i-1}^{2}\right)\left(\delta_{i,j}-2x_{i-1}\delta_{i-1,j}\right)-2\left(1-x_{i-1}\right)\delta_{i-1,j}.\\ & = & 200\left(x_{j}-x_{j-1}^{2}\right)-400x_{j}\left(x_{j+1}-x_{j}^{2}\right)-2\left(1-x_{j}\right).\end{eqnarray*}

Это выражение справедливо для внутренних производных. Особые случаи —

\begin{eqnarray*} \frac{\partial f}{\partial x_{0}} & = & -400x_{0}\left(x_{1}-x_{0}^{2}\right)-2\left(1-x_{0}\right),\\ \frac{\partial f}{\partial x_{N-1}} & = & 200\left(x_{N-1}-x_{N-2}^{2}\right).\end{eqnarray*}

Функция Python, вычисляющая этот градиент, создаётся сегментом кода:

>>> def rosen_der(x):
...     xm = x[1:-1]
...     xm_m1 = x[:-2]
...     xm_p1 = x[2:]
...     der = np.zeros_like(x)
...     der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)
...     der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])
...     der[-1] = 200*(x[-1]-x[-2]**2)
...     return der

Эта информация о градиенте указана в minimize функция через jac параметр, как показано ниже.

>>> res = minimize(rosen, x0, method='BFGS', jac=rosen_der,
...                options={'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 25                     # may vary
         Function evaluations: 30
         Gradient evaluations: 30
>>> res.x
array([1., 1., 1., 1., 1.])

Избежание избыточных вычислений

Часто целевая функция и её градиент используют общие части вычислений. Например, рассмотрим следующую задачу.

>>> def f(x):
...    return -expensive(x[0])**2
>>>
>>> def df(x):
...     return -2 * expensive(x[0]) * dexpensive(x[0])
>>>
>>> def expensive(x):
...     # this function is computationally expensive!
...     expensive.count += 1  # let's keep track of how many times it runs
...     return np.sin(x)
>>> expensive.count = 0
>>>
>>> def dexpensive(x):
...     return np.cos(x)
>>>
>>> res = minimize(f, 0.5, jac=df)
>>> res.fun
-0.9999999999999174
>>> res.nfev, res.njev
6, 6
>>> expensive.count
12

Здесь, expensive вызывается 12 раз: шесть раз в целевой функции и шесть раз из градиента. Один из способов уменьшить избыточные вычисления — создать единую функцию, которая возвращает и целевую функцию, и градиент.

>>> def f_and_df(x):
...     expensive_value = expensive(x[0])
...     return (-expensive_value**2,  # objective function
...             -2*expensive_value*dexpensive(x[0]))  # gradient
>>>
>>> expensive.count = 0  # reset the counter
>>> res = minimize(f_and_df, 0.5, jac=True)
>>> res.fun
-0.9999999999999174
>>> expensive.count
6

Когда мы вызываем minimize, мы указываем jac==True чтобы указать, что предоставленная функция возвращает как целевую функцию, так и её градиент. Хотя удобно, не все scipy.optimize функции поддерживают эту возможность, и более того, это только для совместного использования вычислений между функцией и её градиентом, тогда как в некоторых задачах мы захотим совместно использовать вычисления с гессианом (второй производной целевой функции) и ограничениями. Более общий подход — мемоизация дорогих частей вычисления. В простых ситуациях это можно выполнить с помощью functools.lru_cache обертка.

>>> from functools import lru_cache
>>> expensive.count = 0  # reset the counter
>>> expensive = lru_cache(expensive)
>>> res = minimize(f, 0.5, jac=df)
>>> res.fun
-0.9999999999999174
>>> expensive.count
6

Алгоритм Ньютона-сопряжённых градиентов (method='Newton-CG')

Алгоритм Ньютона-Сопряженных Градиентов является модифицированным методом Ньютона и использует алгоритм сопряженных градиентов для (приближенного) обращения локальной матрицы Гессе [NW]. Метод Ньютона основан на локальной аппроксимации функции квадратичной формой:

\[f\left(\mathbf{x}\right)\approx f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)\cdot\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2}\left(\mathbf{x}-\mathbf{x}_{0}\right)^{T}\mathbf{H}\left(\mathbf{x}_{0}\right)\left(\mathbf{x}-\mathbf{x}_{0}\right).\]

где \(\mathbf{H}\left(\mathbf{x}_{0}\right)\) является матрицей вторых производных (гессиан). Если гессиан положительно определён, то локальный минимум этой функции может быть найден путём приравнивания градиента квадратичной формы к нулю, что даёт

\[\mathbf{x}_{\textrm{opt}}=\mathbf{x}_{0}-\mathbf{H}^{-1}\nabla f.\]

Обратная матрица Гессе вычисляется с использованием метода сопряженных градиентов. Пример использования этого метода для минимизации функции Розенброка приведен ниже. Чтобы в полной мере использовать метод Ньютона-КГ, должна быть предоставлена функция, вычисляющая матрицу Гессе. Сама матрица Гессе не обязательно должна быть построена, требуется только вектор, который является произведением матрицы Гессе на произвольный вектор, доступный для процедуры минимизации. В результате пользователь может предоставить либо функцию для вычисления матрицы Гессе, либо функцию для вычисления произведения матрицы Гессе на произвольный вектор.

Пример полной матрицы Гессе

Гессиан функции Розенброка равен

\begin{eqnarray*} H_{ij}=\frac{\partial^{2}f}{\partial x_{i}\partial x_{j}} & = & 200\left(\delta_{i,j}-2x_{i-1}\delta_{i-1,j}\right)-400x_{i}\left(\delta_{i+1,j}-2x_{i}\delta_{i,j}\right)-400\delta_{i,j}\left(x_{i+1}-x_{i}^{2}\right)+2\delta_{i,j},\\ & = & \left(202+1200x_{i}^{2}-400x_{i+1}\right)\delta_{i,j}-400x_{i}\delta_{i+1,j}-400x_{i-1}\delta_{i-1,j},\end{eqnarray*}

if \(i,j\in\left[1,N-2\right]\) с \(i,j\in\left[0,N-1\right]\) определяющий \(N\times N\) матрицы. Другие ненулевые элементы матрицы

\begin{eqnarray*} \frac{\partial^{2}f}{\partial x_{0}^{2}} & = & 1200x_{0}^{2}-400x_{1}+2,\\ \frac{\partial^{2}f}{\partial x_{0}\partial x_{1}}=\frac{\partial^{2}f}{\partial x_{1}\partial x_{0}} & = & -400x_{0},\\ \frac{\partial^{2}f}{\partial x_{N-1}\partial x_{N-2}}=\frac{\partial^{2}f}{\partial x_{N-2}\partial x_{N-1}} & = & -400x_{N-2},\\ \frac{\partial^{2}f}{\partial x_{N-1}^{2}} & = & 200.\end{eqnarray*}

Например, гессиан, когда \(N=5\) является

\[\begin{split}\mathbf{H}=\begin{bmatrix} 1200x_{0}^{2}+2\mkern-2em\\&1200x_{1}^{2}+202\mkern-2em\\&&1200x_{1}^{2}+202\mkern-2em\\&&&1200x_{3}^{2}+202\mkern-1em\\&&&&200\end{bmatrix}-400\begin{bmatrix} x_1 & x_0 \\ x_0 & x_2 & x_1 \\ & x_1 & x_3 & x_2\\ & & x_2 & x_4 & x_3 \\ & & & x_3 & 0\end{bmatrix}.\end{split}\]

Код, вычисляющий этот гессиан, вместе с кодом для минимизации функции методом Ньютона-КГ, показан в следующем примере:

>>> def rosen_hess(x):
...     x = np.asarray(x)
...     H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)
...     diagonal = np.zeros_like(x)
...     diagonal[0] = 1200*x[0]**2-400*x[1]+2
...     diagonal[-1] = 200
...     diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]
...     H = H + np.diag(diagonal)
...     return H

>>> res = minimize(rosen, x0, method='Newton-CG',
...                jac=rosen_der, hess=rosen_hess,
...                options={'xtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                       # may vary
         Function evaluations: 22
         Gradient evaluations: 19
         Hessian evaluations: 19
>>> res.x
array([1.,  1.,  1.,  1.,  1.])

Пример произведения гессиана

Для больших задач минимизации хранение всей матрицы Гессе может занимать значительное время и память. Алгоритм Newton-CG нуждается только в произведении матрицы Гессе на произвольный вектор. В результате пользователь может предоставить код для вычисления этого произведения вместо полной матрицы Гессе, указав hess функция, которая принимает вектор минимизации как первый аргумент и произвольный вектор как второй аргумент (вместе с дополнительными аргументами, передаваемыми минимизируемой функции). Если возможно, использование Newton-CG с опцией произведения Гессе, вероятно, самый быстрый способ минимизировать функцию.

В этом случае произведение гессиана Розенброка на произвольный вектор несложно вычислить. Если \(\mathbf{p}\) является произвольным вектором, тогда \(\mathbf{H}\left(\mathbf{x}\right)\mathbf{p}\) имеет элементы:

\[\begin{split}\mathbf{H}\left(\mathbf{x}\right)\mathbf{p}=\begin{bmatrix} \left(1200x_{0}^{2}-400x_{1}+2\right)p_{0}-400x_{0}p_{1}\\ \vdots\\ -400x_{i-1}p_{i-1}+\left(202+1200x_{i}^{2}-400x_{i+1}\right)p_{i}-400x_{i}p_{i+1}\\ \vdots\\ -400x_{N-2}p_{N-2}+200p_{N-1}\end{bmatrix}.\end{split}\]

Код, который использует это произведение Гессе для минимизации функции Розенброка с помощью minimize следует:

>>> def rosen_hess_p(x, p):
...     x = np.asarray(x)
...     Hp = np.zeros_like(x)
...     Hp[0] = (1200*x[0]**2 - 400*x[1] + 2)*p[0] - 400*x[0]*p[1]
...     Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] \
...                -400*x[1:-1]*p[2:]
...     Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1]
...     return Hp

>>> res = minimize(rosen, x0, method='Newton-CG',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'xtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 23
         Gradient evaluations: 20
         Hessian evaluations: 44
>>> res.x
array([1., 1., 1., 1., 1.])

Согласно [NW] стр. 170 Newton-CG алгоритм может быть неэффективным, когда матрица Гессе плохо обусловлена из-за низкого качества направлений поиска, предоставляемых методом в таких ситуациях. Метод trust-ncg, по мнению авторов, более эффективно справляется с этой проблемной ситуацией и будет описан далее.

Алгоритм Ньютона-сопряженных градиентов в доверительной области (method='trust-ncg')

The Newton-CG метод является методом поиска по линии: он находит направление поиска, минимизирующее квадратичную аппроксимацию функции, а затем использует алгоритм поиска по линии, чтобы найти (почти) оптимальный размер шага в этом направлении. Альтернативный подход заключается в том, чтобы сначала зафиксировать предел размера шага \(\Delta\) и затем найти оптимальный шаг \(\mathbf{p}\) внутри заданного радиуса доверия путем решения следующей квадратичной подзадачи:

\begin{eqnarray*} \min_{\mathbf{p}} f\left(\mathbf{x}_{k}\right)+\nabla f\left(\mathbf{x}_{k}\right)\cdot\mathbf{p}+\frac{1}{2}\mathbf{p}^{T}\mathbf{H}\left(\mathbf{x}_{k}\right)\mathbf{p};&\\ \text{subject to: } \|\mathbf{p}\|\le \Delta.& \end{eqnarray*}

Затем решение обновляется \(\mathbf{x}_{k+1} = \mathbf{x}_{k} + \mathbf{p}\) и радиус доверия \(\Delta\) корректируется в соответствии со степенью согласия квадратичной модели с реальной функцией. Это семейство методов известно как методы доверительной области. Метод trust-ncg алгоритм — это метод области доверия, который использует алгоритм сопряжённых градиентов для решения подзадачи области доверия [NW].

Пример полной матрицы Гессе

>>> res = minimize(rosen, x0, method='trust-ncg',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 19
>>> res.x
array([1., 1., 1., 1., 1.])

Пример произведения гессиана

>>> res = minimize(rosen, x0, method='trust-ncg',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 20                    # may vary
         Function evaluations: 21
         Gradient evaluations: 20
         Hessian evaluations: 0
>>> res.x
array([1., 1., 1., 1., 1.])

Алгоритм Trust-Region Truncated Generalized Lanczos / Conjugate Gradient (method='trust-krylov')

Аналогично trust-ncg метод, trust-krylov метод подходит для задач большого масштаба, так как использует гессиан только как линейный оператор посредством матрично-векторных произведений. Он решает квадратичную подзадачу точнее, чем trust-ncg метод.

\begin{eqnarray*} \min_{\mathbf{p}} f\left(\mathbf{x}_{k}\right)+\nabla f\left(\mathbf{x}_{k}\right)\cdot\mathbf{p}+\frac{1}{2}\mathbf{p}^{T}\mathbf{H}\left(\mathbf{x}_{k}\right)\mathbf{p};&\\ \text{subject to: } \|\mathbf{p}\|\le \Delta.& \end{eqnarray*}

Этот метод оборачивает [TRLIB] реализация [GLTR] метод, решающий точно подзадачу доверительной области, ограниченную усеченным подпространством Крылова. Для неопределенных задач обычно лучше использовать этот метод, так как он уменьшает количество нелинейных итераций за счет нескольких дополнительных произведений матрицы на вектор на решение подзадачи по сравнению с trust-ncg метод.

Пример полной матрицы Гессе

>>> res = minimize(rosen, x0, method='trust-krylov',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                    # may vary
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 18
>>> res.x
array([1., 1., 1., 1., 1.])

Пример произведения гессиана

>>> res = minimize(rosen, x0, method='trust-krylov',
...                jac=rosen_der, hessp=rosen_hess_p,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19                    # may vary
         Function evaluations: 20
         Gradient evaluations: 20
         Hessian evaluations: 0
>>> res.x
array([1., 1., 1., 1., 1.])

[TRLIB]

F. Lenders, C. Kirches, A. Potschka: "trlib: векторная реализация метода GLTR для итерационного решения задачи доверительной области", arXiv:1611.04718

[GLTR]

N. Gould, S. Lucidi, M. Roma, P. Toint: «Решение подзадачи доверительной области с использованием метода Ланцоша», SIAM J. Optim., 9(2), 504–525, (1999). DOI:10.1137/S1052623497322735

Алгоритм почти точного доверительного региона (method='trust-exact')

Все методы Newton-CG, trust-ncg и trust-krylov подходят для работы с крупномасштабными задачами (задачами с тысячами переменных). Это потому, что алгоритм сопряжённых градиентов приближённо решает подзадачу доверительной области (или инвертирует гессиан) итерациями без явной факторизации гессиана. Поскольку требуется только произведение гессиана на произвольный вектор, алгоритм особенно подходит для работы с разреженными гессианами, позволяя низкие требования к хранению и значительную экономию времени для этих разреженных задач.

Для задач среднего размера, для которых затраты на хранение и факторизацию гессиана не критичны, возможно получить решение за меньшее количество итераций, решая подзадачи доверительной области почти точно. Для этого определённое нелинейное уравнение решается итеративно для каждой квадратичной подзадачи [CGT]. Это решение обычно требует 3 или 4 разложений Холецкого матрицы Гессе. В результате метод сходится за меньшее число итераций и требует меньше вычислений целевой функции, чем другие реализованные методы доверительной области. Опция произведения Гессе не поддерживается этим алгоритмом. Пример использования функции Розенброка:

>>> res = minimize(rosen, x0, method='trust-exact',
...                jac=rosen_der, hess=rosen_hess,
...                options={'gtol': 1e-8, 'disp': True})
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 13                    # may vary
         Function evaluations: 14
         Gradient evaluations: 13
         Hessian evaluations: 14
>>> res.x
array([1., 1., 1., 1., 1.])

[NW] (1,2,3)

Дж. Ноцедал, С.Дж. Райт «Численная оптимизация». 2-е издание. Springer Science (2006).

[CGT]

Conn, A. R., Gould, N. I., & Toint, P. L. “Trust region methods”. Siam. (2000). pp. 169-200.

Ограниченная минимизация

The minimize функция предоставляет несколько алгоритмов для ограниченной минимизации, а именно 'trust-constr' , 'SLSQP', 'COBYLA', и 'COBYQA'. Они требуют, чтобы ограничения были определены с использованием немного разных структур. Методы 'trust-constr', 'COBYQA', и 'COBYLA' требуют, чтобы ограничения были определены как последовательность объектов LinearConstraint и NonlinearConstraint. Метод 'SLSQP', с другой стороны, требует, чтобы ограничения были определены как последовательность словарей, с ключами type, fun и jac.

В качестве примера рассмотрим ограниченную минимизацию функции Розенброка:

\begin{eqnarray*} \min_{x_0, x_1} & ~~100\left(x_{1}-x_{0}^{2}\right)^{2}+\left(1-x_{0}\right)^{2} &\\ \text{subject to: } & x_0 + 2 x_1 \leq 1 & \\ & x_0^2 + x_1 \leq 1 & \\ & x_0^2 - x_1 \leq 1 & \\ & 2 x_0 + x_1 = 1 & \\ & 0 \leq x_0 \leq 1 & \\ & -0.5 \leq x_1 \leq 2.0. & \end{eqnarray*}

Эта задача оптимизации имеет единственное решение \([x_0, x_1] = [0.4149,~ 0.1701]\), для которого активны только первое и четвёртое ограничения.

Алгоритм с ограничениями доверительной области (method='trust-constr')

Метод доверительной области с ограничениями решает задачи минимизации с ограничениями вида:

\begin{eqnarray*} \min_x & f(x) & \\ \text{subject to: } & ~~~ c^l \leq c(x) \leq c^u, &\\ & x^l \leq x \leq x^u. & \end{eqnarray*}

Когда \(c^l_j = c^u_j\) метод читает \(j\)-е ограничение как ограничение равенства и обрабатывает его соответствующим образом. Кроме того, одностороннее ограничение может быть задано установкой верхней или нижней границы в np.inf с соответствующим знаком.

Реализация основана на [EQSQP] для задач с ограничениями-равенствами и на [TRIP] для задач с ограничениями-неравенствами. Оба алгоритма относятся к типу доверительной области и подходят для задач большой размерности.

Определение ограничений границ

Ограничения в виде границ \(0 \leq x_0 \leq 1\) и \(-0.5 \leq x_1 \leq 2.0\) определяются с использованием Bounds объект.

>>> from scipy.optimize import Bounds
>>> bounds = Bounds([0, -0.5], [1.0, 2.0])

Определение линейных ограничений

Ограничения \(x_0 + 2 x_1 \leq 1\) и \(2 x_0 + x_1 = 1\) может быть записано в стандартном формате линейного ограничения:

\begin{equation*} \begin{bmatrix}-\infty \\1\end{bmatrix} \leq \begin{bmatrix} 1& 2 \\ 2& 1\end{bmatrix} \begin{bmatrix} x_0 \\x_1\end{bmatrix} \leq \begin{bmatrix} 1 \\ 1\end{bmatrix},\end{equation*}

и определен с использованием LinearConstraint объект.

>>> from scipy.optimize import LinearConstraint
>>> linear_constraint = LinearConstraint([[1, 2], [2, 1]], [-np.inf, 1], [1, 1])

Определение нелинейных ограничений Нелинейное ограничение:

\begin{equation*} c(x) = \begin{bmatrix} x_0^2 + x_1 \\ x_0^2 - x_1\end{bmatrix} \leq \begin{bmatrix} 1 \\ 1\end{bmatrix}, \end{equation*}

с матрицей Якоби:

\begin{equation*} J(x) = \begin{bmatrix} 2x_0 & 1 \\ 2x_0 & -1\end{bmatrix},\end{equation*}

и линейная комбинация гессианов:

\begin{equation*} H(x, v) = \sum_{i=0}^1 v_i \nabla^2 c_i(x) = v_0\begin{bmatrix} 2 & 0 \\ 0 & 0\end{bmatrix} + v_1\begin{bmatrix} 2 & 0 \\ 0 & 0\end{bmatrix}, \end{equation*}

определяется с использованием NonlinearConstraint объект.

>>> def cons_f(x):
...     return [x[0]**2 + x[1], x[0]**2 - x[1]]
>>> def cons_J(x):
...     return [[2*x[0], 1], [2*x[0], -1]]
>>> def cons_H(x, v):
...     return v[0]*np.array([[2, 0], [0, 0]]) + v[1]*np.array([[2, 0], [0, 0]])
>>> from scipy.optimize import NonlinearConstraint
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess=cons_H)

Кроме того, также возможно определить гессиан \(H(x, v)\) в виде разреженной матрицы,

>>> from scipy.sparse import csc_matrix
>>> def cons_H_sparse(x, v):
...     return v[0]*csc_matrix([[2, 0], [0, 0]]) + v[1]*csc_matrix([[2, 0], [0, 0]])
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1,
...                                            jac=cons_J, hess=cons_H_sparse)

или как LinearOperator объект.

>>> from scipy.sparse.linalg import LinearOperator
>>> def cons_H_linear_operator(x, v):
...     def matvec(p):
...         return np.array([p[0]*2*(v[0]+v[1]), 0])
...     return LinearOperator((2, 2), matvec=matvec)
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1,
...                                           jac=cons_J, hess=cons_H_linear_operator)

Когда вычисляется матрица Гессе \(H(x, v)\) сложно реализовать или вычислительно неосуществимо, можно использовать HessianUpdateStrategy. В настоящее время доступны стратегии: BFGS и SR1.

>>> from scipy.optimize import BFGS
>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess=BFGS())

Альтернативно, гессиан может быть аппроксимирован с использованием конечных разностей.

>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac=cons_J, hess='2-point')

Якобиан ограничений также может быть аппроксимирован конечными разностями. В этом случае, однако, гессиан не может быть вычислен с помощью конечных разностей и должен быть предоставлен пользователем или определен с использованием HessianUpdateStrategy.

>>> nonlinear_constraint = NonlinearConstraint(cons_f, -np.inf, 1, jac='2-point', hess=BFGS())

Решение задачи оптимизации Оптимизационная задача решается с помощью:

>>> x0 = np.array([0.5, 0])
>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hess=rosen_hess,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.016 s.
>>> print(res.x)
[0.41494531 0.17010937]

При необходимости гессиан целевой функции может быть определён с использованием LinearOperator объект,

>>> def rosen_hess_linop(x):
...     def matvec(p):
...         return rosen_hess_p(x, p)
...     return LinearOperator((2, 2), matvec=matvec)
>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hess=rosen_hess_linop,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.018 s.
>>> print(res.x)
[0.41494531 0.17010937]

или произведение Гессе-вектора через параметр hessp.

>>> res = minimize(rosen, x0, method='trust-constr', jac=rosen_der, hessp=rosen_hess_p,
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 8, CG iterations: 7, optimality: 2.99e-09, constraint violation: 1.11e-16, execution time: 0.018 s.
>>> print(res.x)
[0.41494531 0.17010937]

Альтернативно, первые и вторые производные целевой функции могут быть аппроксимированы. Например, гессиан может быть аппроксимирован с помощью SR1 квази-ньютоновское приближение и градиент с конечными разностями.

>>> from scipy.optimize import SR1
>>> res = minimize(rosen, x0, method='trust-constr',  jac="2-point", hess=SR1(),
...                constraints=[linear_constraint, nonlinear_constraint],
...                options={'verbose': 1}, bounds=bounds)
# may vary
`gtol` termination condition is satisfied.
Number of iterations: 12, function evaluations: 24, CG iterations: 7, optimality: 4.48e-09, constraint violation: 0.00e+00, execution time: 0.016 s.
>>> print(res.x)
[0.41494531 0.17010937]

[TRIP]

Бёрд, Ричард Х., Мэри Э. Хрибар и Хорхе Носедал. 1999. Алгоритм внутренней точки для нелинейного программирования большого масштаба. SIAM Journal on Optimization 9.4: 877-900.

[EQSQP]

Лали, Маруча, Хорхе Ноцедал и Тодд Плантега. 1998. О реализации алгоритма для крупномасштабной оптимизации с ограничениями-равенствами. SIAM Journal on Optimization 8.3: 682-706.

Алгоритм последовательного программирования методом наименьших квадратов (SLSQP) (method='SLSQP')

Метод SLSQP работает с задачами условной минимизации вида:

\begin{eqnarray*} \min_x & f(x) \\ \text{subject to: } & c_j(x) = 0 , &j \in \mathcal{E}\\ & c_j(x) \geq 0 , &j \in \mathcal{I}\\ & \text{lb}_i \leq x_i \leq \text{ub}_i , &i = 1,...,N. \end{eqnarray*}

Где \(\mathcal{E}\) или \(\mathcal{I}\) являются наборами индексов, содержащими ограничения равенства и неравенства.

Как линейные, так и нелинейные ограничения определяются как словари с ключами type, fun и jac.

>>> ineq_cons = {'type': 'ineq',
...              'fun' : lambda x: np.array([1 - x[0] - 2*x[1],
...                                          1 - x[0]**2 - x[1],
...                                          1 - x[0]**2 + x[1]]),
...              'jac' : lambda x: np.array([[-1.0, -2.0],
...                                          [-2*x[0], -1.0],
...                                          [-2*x[0], 1.0]])}
>>> eq_cons = {'type': 'eq',
...            'fun' : lambda x: np.array([2*x[0] + x[1] - 1]),
...            'jac' : lambda x: np.array([2.0, 1.0])}

И задача оптимизации решается с помощью:

>>> x0 = np.array([0.5, 0])
>>> res = minimize(rosen, x0, method='SLSQP', jac=rosen_der,
...                constraints=[eq_cons, ineq_cons], options={'ftol': 1e-9, 'disp': True},
...                bounds=bounds)
# may vary
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 0.342717574857755
            Iterations: 5
            Function evaluations: 6
            Gradient evaluations: 5
>>> print(res.x)
[0.41494475 0.1701105 ]

Большинство опций, доступных для метода 'trust-constr' недоступны для 'SLSQP'.

Сравнение решателей локальной минимизации

Найдите решатель, соответствующий вашим требованиям, используя таблицу ниже. Если есть несколько кандидатов, попробуйте несколько и посмотрите, какие из них лучше соответствуют вашим потребностям (например, время выполнения, значение целевой функции).

Решатель	Ограничения границ	Нелинейные ограничения	Использует градиент	Использует гессиан	Использует разреженность
CG			✓
BFGS			✓
dogleg			✓	✓
trust-ncg			✓	✓
trust-krylov			✓	✓
trust-exact			✓	✓
Newton-CG			✓	✓	✓
Nelder-Mead	✓
Пауэлл	✓
L-BFGS-B	✓		✓
TNC	✓		✓
COBYLA	✓	✓
COBYQA	✓	✓
SLSQP	✓	✓	✓
trust-constr	✓	✓	✓	✓	✓

Глобальная оптимизация

Глобальная оптимизация направлена на поиск глобального минимума функции в заданных границах, при наличии потенциально многих локальных минимумов. Обычно глобальные минимизаторы эффективно исследуют пространство параметров, используя локальный минимизатор (например, minimize) под капотом. SciPy содержит ряд хороших глобальных оптимизаторов. Здесь мы используем их на той же целевой функции, а именно (удачно названной) eggholder функция:

>>> def eggholder(x):
...     return (-(x[1] + 47) * np.sin(np.sqrt(abs(x[0]/2 + (x[1]  + 47))))
...             -x[0] * np.sin(np.sqrt(abs(x[0] - (x[1]  + 47)))))

>>> bounds = [(-512, 512), (-512, 512)]

Эта функция выглядит как упаковка для яиц:

>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D

>>> x = np.arange(-512, 513)
>>> y = np.arange(-512, 513)
>>> xgrid, ygrid = np.meshgrid(x, y)
>>> xy = np.stack([xgrid, ygrid])

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> ax.view_init(45, -45)
>>> ax.plot_surface(xgrid, ygrid, eggholder(xy), cmap='terrain')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('y')
>>> ax.set_zlabel('eggholder(x, y)')
>>> plt.show()

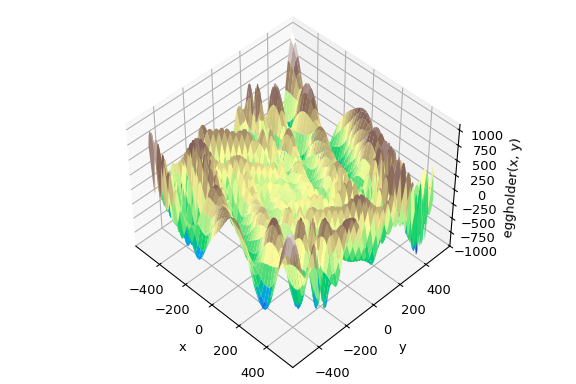
Теперь мы используем глобальные оптимизаторы для получения минимума и значения функции в минимуме. Мы сохраним результаты в словаре, чтобы позже сравнить результаты различных оптимизаций.

>>> from scipy import optimize
>>> results = dict()
>>> results['shgo'] = optimize.shgo(eggholder, bounds)
>>> results['shgo']
     fun: -935.3379515604197  # may vary
    funl: array([-935.33795156])
 message: 'Optimization terminated successfully.'
    nfev: 42
     nit: 2
   nlfev: 37
   nlhev: 0
   nljev: 9
 success: True
       x: array([439.48096952, 453.97740589])
      xl: array([[439.48096952, 453.97740589]])

>>> results['DA'] = optimize.dual_annealing(eggholder, bounds)
>>> results['DA']
     fun: -956.9182316237413  # may vary
 message: ['Maximum number of iteration reached']
    nfev: 4091
    nhev: 0
     nit: 1000
    njev: 0
       x: array([482.35324114, 432.87892901])

Все оптимизаторы возвращают OptimizeResult, который помимо решения содержит информацию о количестве вычислений функции, успешности оптимизации и другие данные. Для краткости мы не будем показывать полный вывод других оптимизаторов:

>>> results['DE'] = optimize.differential_evolution(eggholder, bounds)

shgo имеет второй метод, который возвращает все локальные минимумы, а не только то, что он считает глобальным минимумом:

>>> results['shgo_sobol'] = optimize.shgo(eggholder, bounds, n=200, iters=5,
...                                       sampling_method='sobol')

Теперь построим все найденные минимумы на тепловой карте функции:

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> im = ax.imshow(eggholder(xy), interpolation='bilinear', origin='lower',
...                cmap='gray')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('y')
>>>
>>> def plot_point(res, marker='o', color=None):
...     ax.plot(512+res.x[0], 512+res.x[1], marker=marker, color=color, ms=10)

>>> plot_point(results['DE'], color='c')  # differential_evolution - cyan
>>> plot_point(results['DA'], color='w')  # dual_annealing.        - white

>>> # SHGO produces multiple minima, plot them all (with a smaller marker size)
>>> plot_point(results['shgo'], color='r', marker='+')
>>> plot_point(results['shgo_sobol'], color='r', marker='x')
>>> for i in range(results['shgo_sobol'].xl.shape[0]):
...     ax.plot(512 + results['shgo_sobol'].xl[i, 0],
...             512 + results['shgo_sobol'].xl[i, 1],
...             'ro', ms=2)

>>> ax.set_xlim([-4, 514*2])
>>> ax.set_ylim([-4, 514*2])
>>> plt.show()

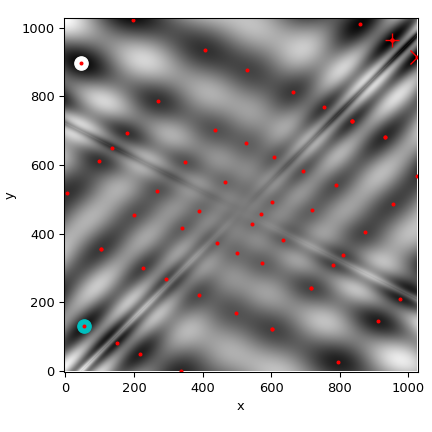
Сравнение глобальных оптимизаторов

Найдите решатель, соответствующий вашим требованиям, используя таблицу ниже. Если есть несколько кандидатов, попробуйте несколько и посмотрите, какие из них лучше соответствуют вашим потребностям (например, время выполнения, значение целевой функции).

Решатель	Ограничения границ	Нелинейные ограничения	Использует градиент	Использует гессиан
basinhopping			(✓)	(✓)
прямой	✓
dual_annealing	✓		(✓)	(✓)
differential_evolution	✓	✓
shgo	✓	✓	(✓)	(✓)

(✓) = В зависимости от выбранного локального минимизатора

Минимизация методом наименьших квадратов (least_squares)

SciPy способен решать робастизированные задачи нелинейного метода наименьших квадратов с ограничениями:

\begin{align} &\min_\mathbf{x} \frac{1}{2} \sum_{i = 1}^m \rho\left(f_i(\mathbf{x})^2\right) \\ &\text{subject to }\mathbf{lb} \leq \mathbf{x} \leq \mathbf{ub} \end{align}

Здесь \(f_i(\mathbf{x})\) являются гладкими функциями из \(\mathbb{R}^n\) to \(\mathbb{R}\), мы называем их остатками. Цель скалярной функции \(\rho(\cdot)\) состоит в уменьшении влияния выбросов в остатках и способствует устойчивости решения, мы называем это функцией потерь. Линейная функция потерь даёт стандартную задачу наименьших квадратов. Кроме того, ограничения в виде нижних и верхних границ для некоторых из \(x_j\) разрешены.

Все методы, специфичные для минимизации наименьших квадратов, используют \(m \times n\) матрица частных производных, называемая якобианом и определяемая как \(J_{ij} = \partial f_i / \partial x_j\). Настоятельно рекомендуется вычислять эту матрицу аналитически и передавать её в least_squaresв противном случае он будет оценен с помощью конечных разностей, что занимает много дополнительного времени и может быть очень неточным в сложных случаях.

Функция least_squares можно использовать для подгонки функции \(\varphi(t; \mathbf{x})\) к эмпирическим данным \(\{(t_i, y_i), i = 0, \ldots, m-1\}\). Для этого следует просто предварительно вычислить остатки как \(f_i(\mathbf{x}) = w_i (\varphi(t_i; \mathbf{x}) - y_i)\), где \(w_i\) — это веса, назначенные каждому наблюдению.

Пример решения задачи подгонки

Здесь мы рассматриваем ферментативную реакцию [1]. Определено 11 остатков как

\[f_i(x) = \frac{x_0 (u_i^2 + u_i x_1)}{u_i^2 + u_i x_2 + x_3} - y_i, \quad i = 0, \ldots, 10,\]

где \(y_i\) являются значениями измерений и \(u_i\) являются значениями независимой переменной. Неизвестный вектор параметров — это \(\mathbf{x} = (x_0, x_1, x_2, x_3)^T\). Как было сказано ранее, рекомендуется вычислять матрицу Якоби в замкнутой форме:

\begin{align} &J_{i0} = \frac{\partial f_i}{\partial x_0} = \frac{u_i^2 + u_i x_1}{u_i^2 + u_i x_2 + x_3} \\ &J_{i1} = \frac{\partial f_i}{\partial x_1} = \frac{u_i x_0}{u_i^2 + u_i x_2 + x_3} \\ &J_{i2} = \frac{\partial f_i}{\partial x_2} = -\frac{x_0 (u_i^2 + u_i x_1) u_i}{(u_i^2 + u_i x_2 + x_3)^2} \\ &J_{i3} = \frac{\partial f_i}{\partial x_3} = -\frac{x_0 (u_i^2 + u_i x_1)}{(u_i^2 + u_i x_2 + x_3)^2} \end{align}

Мы собираемся использовать "сложную" начальную точку, определенную в [2]. Чтобы найти физически значимое решение, избежать потенциального деления на ноль и обеспечить сходимость к глобальному минимуму, мы накладываем ограничения \(0 \leq x_j \leq 100, j = 0, 1, 2, 3\).

Приведённый ниже код реализует оценку методом наименьших квадратов \(\mathbf{x}\) и наконец строит график исходных данных и подобранной модельной функции:

>>> from scipy.optimize import least_squares

>>> def model(x, u):
...     return x[0] * (u ** 2 + x[1] * u) / (u ** 2 + x[2] * u + x[3])

>>> def fun(x, u, y):
...     return model(x, u) - y

>>> def jac(x, u, y):
...     J = np.empty((u.size, x.size))
...     den = u ** 2 + x[2] * u + x[3]
...     num = u ** 2 + x[1] * u
...     J[:, 0] = num / den
...     J[:, 1] = x[0] * u / den
...     J[:, 2] = -x[0] * num * u / den ** 2
...     J[:, 3] = -x[0] * num / den ** 2
...     return J

>>> u = np.array([4.0, 2.0, 1.0, 5.0e-1, 2.5e-1, 1.67e-1, 1.25e-1, 1.0e-1,
...               8.33e-2, 7.14e-2, 6.25e-2])
>>> y = np.array([1.957e-1, 1.947e-1, 1.735e-1, 1.6e-1, 8.44e-2, 6.27e-2,
...               4.56e-2, 3.42e-2, 3.23e-2, 2.35e-2, 2.46e-2])
>>> x0 = np.array([2.5, 3.9, 4.15, 3.9])
>>> res = least_squares(fun, x0, jac=jac, bounds=(0, 100), args=(u, y), verbose=1)
# may vary
`ftol` termination condition is satisfied.
Function evaluations 130, initial cost 4.4383e+00, final cost 1.5375e-04, first-order optimality 4.92e-08.
>>> res.x
array([ 0.19280596,  0.19130423,  0.12306063,  0.13607247])

>>> import matplotlib.pyplot as plt
>>> u_test = np.linspace(0, 5)
>>> y_test = model(res.x, u_test)
>>> plt.plot(u, y, 'o', markersize=4, label='data')
>>> plt.plot(u_test, y_test, label='fitted model')
>>> plt.xlabel("u")
>>> plt.ylabel("y")
>>> plt.legend(loc='lower right')
>>> plt.show()

[1]

J. Kowalik и J. F. Morrison, "Analysis of kinetic data for allosteric enzyme reactions as a nonlinear regression problem", Math. Biosci., vol. 2, pp. 57-66, 1968.

[2]

2. 13. Averick et al., “The MINPACK-2 Test Problem Collection”.

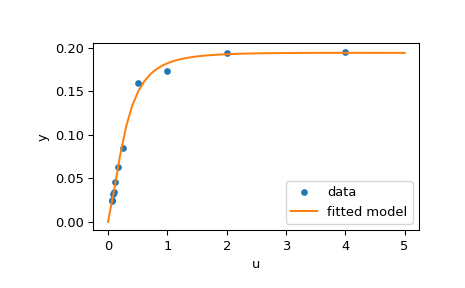
Дополнительные примеры

Три интерактивных примера ниже иллюстрируют использование least_squares более подробно.

1. Крупномасштабная настройка связок в scipy демонстрирует возможности в крупном масштабе least_squares и как эффективно вычислять конечно-разностную аппроксимацию разреженной матрицы Якоби.

2. Робастная нелинейная регрессия в scipy показывает, как обрабатывать выбросы с помощью устойчивой функции потерь в нелинейной регрессии.

3. Решение дискретной краевой задачи в scipy рассматривает, как решить большую систему уравнений и использовать ограничения для достижения желаемых свойств решения.

Для подробностей о математических алгоритмах, лежащих в основе реализации, обратитесь к документации least_squares.

Минимизаторы одномерных функций (minimize_scalar)

Часто требуется только минимум унарной функции (т.е. функции, принимающей скаляр на вход). В таких случаях разработаны другие методы оптимизации, которые могут работать быстрее. Они доступны из minimize_scalar функция, которая предлагает несколько алгоритмов.

Безусловная минимизация (method='brent')

Существуют, фактически, два метода, которые можно использовать для минимизации одномерной функции: brent и golden, но golden включён только в академических целях и должен редко использоваться. Они могут быть выбраны соответственно через метод параметр в minimize_scalar. brent метод использует алгоритм Брента для нахождения минимума. Оптимально, скобка (интервал bracket параметр) должен быть указан, содержащий желаемый минимум. Скобка — это тройка \(\left( a, b, c \right)\) такой, что \(f \left( a \right) > f \left( b \right) < f \left( c \right)\) и \(a < b < c\) . Если это не задано, то можно выбрать две начальные точки, и интервал будет найден из этих точек с помощью простого алгоритма марша. Если эти две начальные точки не предоставлены, 0 и 1 будет использоваться (это может быть неправильным выбором для вашей функции и привести к возврату неожиданного минимума).

Вот пример:

>>> from scipy.optimize import minimize_scalar
>>> f = lambda x: (x - 2) * (x + 1)**2
>>> res = minimize_scalar(f, method='brent')
>>> print(res.x)
1.0

Ограниченная минимизация (method='bounded')

Очень часто существуют ограничения, которые могут быть наложены на пространство решений перед минимизацией. The ограниченный метод в minimize_scalar является примером процедуры ограниченной минимизации, которая предоставляет базовое интервальное ограничение для скалярных функций. Интервальное ограничение позволяет минимизации происходить только между двумя фиксированными конечными точками, заданными с использованием обязательного границы параметр.

Например, чтобы найти минимум \(J_{1}\left( x \right)\) около \(x=5\) , minimize_scalar может быть вызван с использованием интервала \(\left[ 4, 7 \right]\) в качестве ограничения. Результатом является \(x_{\textrm{min}}=5.3314\) :

>>> from scipy.special import j1
>>> res = minimize_scalar(j1, bounds=(4, 7), method='bounded')
>>> res.x
5.33144184241

Пользовательские минимизаторы

Иногда может быть полезно использовать пользовательский метод в качестве (многомерного или одномерного) минимизатора, например, при использовании некоторых библиотечных обёрток minimize (например, basinhopping).

Мы можем достичь этого, вместо передачи имени метода, передавая вызываемый объект (либо функцию, либо объект, реализующий __call__ метод) как метод параметр.

Рассмотрим (довольно виртуальную) необходимость использования тривиального пользовательского метода многомерной минимизации, который будет просто искать окрестность в каждом измерении независимо с фиксированным размером шага:

>>> from scipy.optimize import OptimizeResult
>>> def custmin(fun, x0, args=(), maxfev=None, stepsize=0.1,
...         maxiter=100, callback=None, **options):
...     bestx = x0
...     besty = fun(x0)
...     funcalls = 1
...     niter = 0
...     improved = True
...     stop = False
...
...     while improved and not stop and niter < maxiter:
...         improved = False
...         niter += 1
...         for dim in range(np.size(x0)):
...             for s in [bestx[dim] - stepsize, bestx[dim] + stepsize]:
...                 testx = np.copy(bestx)
...                 testx[dim] = s
...                 testy = fun(testx, *args)
...                 funcalls += 1
...                 if testy < besty:
...                     besty = testy
...                     bestx = testx
...                     improved = True
...             if callback is not None:
...                 callback(bestx)
...             if maxfev is not None and funcalls >= maxfev:
...                 stop = True
...                 break
...
...     return OptimizeResult(fun=besty, x=bestx, nit=niter,
...                           nfev=funcalls, success=(niter > 1))
>>> x0 = [1.35, 0.9, 0.8, 1.1, 1.2]
>>> res = minimize(rosen, x0, method=custmin, options=dict(stepsize=0.05))
>>> res.x
array([1., 1., 1., 1., 1.])

Это будет работать так же хорошо в случае одномерной оптимизации:

>>> def custmin(fun, bracket, args=(), maxfev=None, stepsize=0.1,
...         maxiter=100, callback=None, **options):
...     bestx = (bracket[1] + bracket[0]) / 2.0
...     besty = fun(bestx)
...     funcalls = 1
...     niter = 0
...     improved = True
...     stop = False
...
...     while improved and not stop and niter < maxiter:
...         improved = False
...         niter += 1
...         for testx in [bestx - stepsize, bestx + stepsize]:
...             testy = fun(testx, *args)
...             funcalls += 1
...             if testy < besty:
...                 besty = testy
...                 bestx = testx
...                 improved = True
...         if callback is not None:
...             callback(bestx)
...         if maxfev is not None and funcalls >= maxfev:
...             stop = True
...             break
...
...     return OptimizeResult(fun=besty, x=bestx, nit=niter,
...                           nfev=funcalls, success=(niter > 1))
>>> def f(x):
...    return (x - 2)**2 * (x + 2)**2
>>> res = minimize_scalar(f, bracket=(-3.5, 0), method=custmin,
...                       options=dict(stepsize = 0.05))
>>> res.x
-2.0

Нахождение корней

Скалярные функции

Если имеется уравнение с одной переменной, можно попробовать несколько различных алгоритмов поиска корней. Большинство этих алгоритмов требуют конечные точки интервала, в котором ожидается корень (поскольку функция меняет знак). В общем случае, brentq является наилучшим выбором, но другие методы могут быть полезны в определённых обстоятельствах или для академических целей. Когда скобка недоступна, но доступна одна или несколько производных, тогда newton (или halley, secant) может быть применим. Это особенно актуально, если функция определена на подмножестве комплексной плоскости, и методы скобок не могут быть использованы.

Решение с фиксированной точкой

Проблема, тесно связанная с нахождением нулей функции, — это проблема нахождения неподвижной точки функции. Неподвижная точка функции — это точка, в которой вычисление функции возвращает ту же точку: \(g\left(x\right)=x.\) Очевидно, что неподвижная точка \(g\) является корнем \(f\left(x\right)=g\left(x\right)-x.\) Эквивалентно, корень \(f\) является неподвижной точкой \(g\left(x\right)=f\left(x\right)+x.\) Подпрограмма fixed_point предоставляет простой итеративный метод с использованием ускорения последовательности Айткена для оценки неподвижной точки \(g\) заданной начальной точкой.

Системы уравнений

Нахождение корня системы нелинейных уравнений может быть достигнуто с использованием root функция. Доступно несколько методов, среди которых hybr (по умолчанию) и lm, которые соответственно используют гибридный метод Пауэлла и метод Левенберга-Марквардта из MINPACK.

Следующий пример рассматривает трансцендентное уравнение с одной переменной

\[x+2\cos\left(x\right)=0,\]

корень которого можно найти следующим образом:

>>> import numpy as np
>>> from scipy.optimize import root
>>> def func(x):
...     return x + 2 * np.cos(x)
>>> sol = root(func, 0.3)
>>> sol.x
array([-1.02986653])
>>> sol.fun
array([ -6.66133815e-16])

Рассмотрим теперь систему нелинейных уравнений

\begin{eqnarray*} x_{0}\cos\left(x_{1}\right) & = & 4,\\ x_{0}x_{1}-x_{1} & = & 5. \end{eqnarray*}

Мы определяем целевую функцию так, чтобы она также возвращала матрицу Якоби, и указываем это, устанавливая jac параметр для True. Также здесь используется решатель Левенберга-Марквардта.

>>> def func2(x):
...     f = [x[0] * np.cos(x[1]) - 4,
...          x[1]*x[0] - x[1] - 5]
...     df = np.array([[np.cos(x[1]), -x[0] * np.sin(x[1])],
...                    [x[1], x[0] - 1]])
...     return f, df
>>> sol = root(func2, [1, 1], jac=True, method='lm')
>>> sol.x
array([ 6.50409711,  0.90841421])

Поиск корней для больших задач

Методы hybr и lm в root не может работать с очень большим количеством переменных (N), так как им необходимо вычислять и инвертировать плотную N x N матрицы Якоби на каждом шаге Ньютона. Это становится довольно неэффективным, когда N растет.

Рассмотрим, например, следующую задачу: нужно решить следующее интегро-дифференциальное уравнение на квадрате \([0,1]\times[0,1]\):

\[(\partial_x^2 + \partial_y^2) P + 5 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2 = 0\]

с граничным условием \(P(x,1) = 1\) на верхнем крае и \(P=0\) в других местах на границе квадрата. Это можно сделать путем аппроксимации непрерывной функции P по его значениям на сетке, \(P_{n,m}\approx{}P(n h, m h)\), с малым шагом сетки h. Производные и интегралы затем могут быть аппроксимированы; например \(\partial_x^2 P(x,y)\approx{}(P(x+h,y) - 2 P(x,y) + P(x-h,y))/h^2\). Задача тогда эквивалентна нахождению корня некоторой функции residual(P), где P является вектором длины \(N_x N_y\).

Теперь, поскольку \(N_x N_y\) может быть большим, методы hybr или lm в root потребует много времени для решения этой задачи. Однако решение может быть найдено с использованием одного из решателей для больших задач, например krylov, broyden2, или anderson. Они используют так называемый неточный метод Ньютона, который вместо точного вычисления матрицы Якоби формирует её аппроксимацию.

Теперь нашу задачу можно решить следующим образом:

import numpy as np
from scipy.optimize import root
from numpy import cosh, zeros_like, mgrid, zeros

# parameters
nx, ny = 75, 75
hx, hy = 1./(nx-1), 1./(ny-1)

P_left, P_right = 0, 0
P_top, P_bottom = 1, 0

def residual(P):
   d2x = zeros_like(P)
   d2y = zeros_like(P)

   d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2]) / hx/hx
   d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
   d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx

   d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
   d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
   d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy

   return d2x + d2y + 5*cosh(P).mean()**2

# solve
guess = zeros((nx, ny), float)
sol = root(residual, guess, method='krylov', options={'disp': True})
#sol = root(residual, guess, method='broyden2', options={'disp': True, 'max_rank': 50})
#sol = root(residual, guess, method='anderson', options={'disp': True, 'M': 10})
print('Residual: %g' % abs(residual(sol.x)).max())

# visualize
import matplotlib.pyplot as plt
x, y = mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
plt.pcolormesh(x, y, sol.x, shading='gouraud')
plt.colorbar()
plt.show()

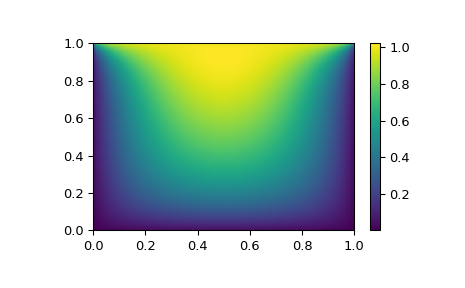
Все еще слишком медленно? Предварительная обработка.

При поиске нуля функций \(f_i({\bf x}) = 0\), i = 1, 2, …, N, krylov решатель тратит большую часть времени на инвертирование матрицы Якоби,

\[J_{ij} = \frac{\partial f_i}{\partial x_j} .\]

Если у вас есть приближение для обратной матрицы \(M\approx{}J^{-1}\), вы можете использовать его для предобусловливание линейной задачи обращения. Идея заключается в том, что вместо решения \(J{\bf s}={\bf y}\) решается \(MJ{\bf s}=M{\bf y}\): поскольку матрица \(MJ\) является "ближе" к единичной матрице, чем \(J\) то есть, уравнение должно быть проще для метода Крылова.

Матрица M может быть передан в root с методом krylov как опция options['jac_options']['inner_M']. Это может быть (разреженная) матрица или scipy.sparse.linalg.LinearOperator экземпляр.

Для задачи из предыдущего раздела отметим, что решаемая функция состоит из двух частей: первая — применение оператора Лапласа, \([\partial_x^2 + \partial_y^2] P\), а второй - интеграл. Мы можем легко вычислить якобиан, соответствующий части оператора Лапласа: мы знаем, что в 1-D

\[\begin{split}\partial_x^2 \approx \frac{1}{h_x^2} \begin{pmatrix} -2 & 1 & 0 & 0 \cdots \\ 1 & -2 & 1 & 0 \cdots \\ 0 & 1 & -2 & 1 \cdots \\ \ldots \end{pmatrix} = h_x^{-2} L\end{split}\]

так что весь 2-D оператор представлен

\[J_1 = \partial_x^2 + \partial_y^2 \simeq h_x^{-2} L \otimes I + h_y^{-2} I \otimes L\]

Матрица \(J_2\) якобиана, соответствующего интегралу, сложнее вычислить, и поскольку все если его записи ненулевые, будет сложно инвертировать. \(J_1\) с другой стороны является относительно простой матрицей и может быть обращена с помощью scipy.sparse.linalg.splu (или обратное может быть аппроксимировано с помощью scipy.sparse.linalg.spilu). Поэтому мы довольствуемся взятием \(M\approx{}J_1^{-1}\) и надеяться на лучшее.

В примере ниже мы используем предобуславливатель \(M=J_1^{-1}\).

from scipy.optimize import root
from scipy.sparse import dia_array, kron
from scipy.sparse.linalg import spilu, LinearOperator
from numpy import cosh, zeros_like, mgrid, zeros, eye

# parameters
nx, ny = 75, 75
hx, hy = 1./(nx-1), 1./(ny-1)

P_left, P_right = 0, 0
P_top, P_bottom = 1, 0

def get_preconditioner():
    """Compute the preconditioner M"""
    diags_x = zeros((3, nx))
    diags_x[0,:] = 1/hx/hx
    diags_x[1,:] = -2/hx/hx
    diags_x[2,:] = 1/hx/hx
    Lx = dia_array((diags_x, [-1,0,1]), shape=(nx, nx))

    diags_y = zeros((3, ny))
    diags_y[0,:] = 1/hy/hy
    diags_y[1,:] = -2/hy/hy
    diags_y[2,:] = 1/hy/hy
    Ly = dia_array((diags_y, [-1,0,1]), shape=(ny, ny))

    J1 = kron(Lx, eye(ny)) + kron(eye(nx), Ly)

    # Now we have the matrix `J_1`. We need to find its inverse `M` --
    # however, since an approximate inverse is enough, we can use
    # the *incomplete LU* decomposition

    J1_ilu = spilu(J1)

    # This returns an object with a method .solve() that evaluates
    # the corresponding matrix-vector product. We need to wrap it into
    # a LinearOperator before it can be passed to the Krylov methods:

    M = LinearOperator(shape=(nx*ny, nx*ny), matvec=J1_ilu.solve)
    return M

def solve(preconditioning=True):
    """Compute the solution"""
    count = [0]

    def residual(P):
        count[0] += 1

        d2x = zeros_like(P)
        d2y = zeros_like(P)

        d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2])/hx/hx
        d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
        d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx

        d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
        d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
        d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy

        return d2x + d2y + 5*cosh(P).mean()**2

    # preconditioner
    if preconditioning:
        M = get_preconditioner()
    else:
        M = None

    # solve
    guess = zeros((nx, ny), float)

    sol = root(residual, guess, method='krylov',
               options={'disp': True,
                        'jac_options': {'inner_M': M}})
    print('Residual', abs(residual(sol.x)).max())
    print('Evaluations', count[0])

    return sol.x

def main():
    sol = solve(preconditioning=True)

    # visualize
    import matplotlib.pyplot as plt
    x, y = mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
    plt.clf()
    plt.pcolor(x, y, sol)
    plt.clim(0, 1)
    plt.colorbar()
    plt.show()


if __name__ == "__main__":
    main()

Результат выполнения, сначала без предобусловливания:

0:  |F(x)| = 803.614; step 1; tol 0.000257947
1:  |F(x)| = 345.912; step 1; tol 0.166755
2:  |F(x)| = 139.159; step 1; tol 0.145657
3:  |F(x)| = 27.3682; step 1; tol 0.0348109
4:  |F(x)| = 1.03303; step 1; tol 0.00128227
5:  |F(x)| = 0.0406634; step 1; tol 0.00139451
6:  |F(x)| = 0.00344341; step 1; tol 0.00645373
7:  |F(x)| = 0.000153671; step 1; tol 0.00179246
8:  |F(x)| = 6.7424e-06; step 1; tol 0.00173256
Residual 3.57078908664e-07
Evaluations 317

и затем с предобусловливанием:

0:  |F(x)| = 136.993; step 1; tol 7.49599e-06
1:  |F(x)| = 4.80983; step 1; tol 0.00110945
2:  |F(x)| = 0.195942; step 1; tol 0.00149362
3:  |F(x)| = 0.000563597; step 1; tol 7.44604e-06
4:  |F(x)| = 1.00698e-09; step 1; tol 2.87308e-12
Residual 9.29603061195e-11
Evaluations 77

Использование предобуславливателя сократило количество вычислений residual функции на коэффициент 4. Для задач, где остаток дорого вычислять, хорошее предобуславливание может быть критически важным — оно может даже решить, решаема ли задача на практике или нет.

Предобусловливание — это искусство, наука и индустрия. Здесь нам повезло с простым выбором, который сработал достаточно хорошо, но эта тема гораздо глубже, чем показано здесь.

Линейное программирование (linprog)

Функция linprog может минимизировать линейную целевую функцию при линейных ограничениях равенства и неравенства. Такая задача хорошо известна как линейное программирование. Линейное программирование решает задачи следующего вида:

\[\begin{split}\min_x \ & c^T x \\ \mbox{such that} \ & A_{ub} x \leq b_{ub},\\ & A_{eq} x = b_{eq},\\ & l \leq x \leq u ,\end{split}\]

где \(x\) является вектором переменных решения; \(c\), \(b_{ub}\), \(b_{eq}\), \(l\), и \(u\) являются векторами; и \(A_{ub}\) и \(A_{eq}\) являются матрицами.

В этом руководстве мы попытаемся решить типичную задачу линейного программирования с использованием linprog.

Пример линейного программирования

Рассмотрим следующую простую задачу линейного программирования:

\[\begin{split}\max_{x_1, x_2, x_3, x_4} \ & 29x_1 + 45x_2 \\ \mbox{such that} \ & x_1 -x_2 -3x_3 \leq 5\\ & 2x_1 -3x_2 -7x_3 + 3x_4 \geq 10\\ & 2x_1 + 8x_2 + x_3 = 60\\ & 4x_1 + 4x_2 + x_4 = 60\\ & 0 \leq x_0\\ & 0 \leq x_1 \leq 5\\ & x_2 \leq 0.5\\ & -3 \leq x_3\\\end{split}\]

Нам нужны некоторые математические преобразования, чтобы привести целевую задачу к форме, принимаемой linprog.

Прежде всего, рассмотрим целевую функцию. Мы хотим максимизировать целевую функцию, но linprog может принимать только задачу минимизации. Это легко исправить, преобразовав максимизацию \(29x_1 + 45x_2\) к минимизации \(-29x_1 -45x_2\). Также, \(x_3, x_4\) не отображаются в целевой функции. Это означает, что веса, соответствующие \(x_3, x_4\) равны нулю. Таким образом, целевую функцию можно преобразовать в:

\[\min_{x_1, x_2, x_3, x_4} \ -29x_1 -45x_2 + 0x_3 + 0x_4\]

Если мы определим вектор переменных решения \(x = [x_1, x_2, x_3, x_4]^T\), вектор весов целевой функции \(c\) of linprog в этой задаче должно быть

\[c = [-29, -45, 0, 0]^T\]

Далее рассмотрим два ограничения-неравенства. Первое — это неравенство 'меньше', поэтому оно уже в форме, принимаемой linprog. Второе - неравенство "больше чем", поэтому нужно умножить обе стороны на \(-1\) для преобразования в неравенство «меньше». Явно показывая нулевые коэффициенты, имеем:

\[\begin{split}x_1 -x_2 -3x_3 + 0x_4 &\leq 5\\ -2x_1 + 3x_2 + 7x_3 - 3x_4 &\leq -10\\\end{split}\]

Эти уравнения могут быть преобразованы в матричную форму:

\[\begin{split}A_{ub} x \leq b_{ub}\\\end{split}\]

где

\begin{equation*} A_{ub} = \begin{bmatrix} 1 & -1 & -3 & 0 \\ -2 & 3 & 7 & -3 \end{bmatrix} \end{equation*}

\begin{equation*} b_{ub} = \begin{bmatrix} 5 \\ -10 \end{bmatrix} \end{equation*}

Далее рассмотрим два ограничения равенства. Показывая нулевые веса явно, они выглядят так:

\[\begin{split}2x_1 + 8x_2 + 1x_3 + 0x_4 &= 60\\ 4x_1 + 4x_2 + 0x_3 + 1x_4 &= 60\\\end{split}\]

Эти уравнения могут быть преобразованы в матричную форму:

\[\begin{split}A_{eq} x = b_{eq}\\\end{split}\]

где

\begin{equation*} A_{eq} = \begin{bmatrix} 2 & 8 & 1 & 0 \\ 4 & 4 & 0 & 1 \end{bmatrix} \end{equation*}

\begin{equation*} b_{eq} = \begin{bmatrix} 60 \\ 60 \end{bmatrix} \end{equation*}

Наконец, рассмотрим отдельные ограничения-неравенства на отдельные переменные решения, которые известны как "ограничения типа коробки" или "простые границы". Эти ограничения могут быть применены с помощью аргумента bounds в linprog. Как отмечено в linprog документации, значение по умолчанию для bounds - (0, None), что означает, что нижняя граница каждой переменной решения равна 0, а верхняя граница каждой переменной решения равна бесконечности: все переменные решения неотрицательны. Наши границы отличаются, поэтому нам нужно указать нижнюю и верхнюю границы для каждой переменной решения в виде кортежа и сгруппировать эти кортежи в список.

Наконец, мы можем решить преобразованную задачу с помощью linprog.

>>> import numpy as np
>>> from scipy.optimize import linprog
>>> c = np.array([-29.0, -45.0, 0.0, 0.0])
>>> A_ub = np.array([[1.0, -1.0, -3.0, 0.0],
...                 [-2.0, 3.0, 7.0, -3.0]])
>>> b_ub = np.array([5.0, -10.0])
>>> A_eq = np.array([[2.0, 8.0, 1.0, 0.0],
...                 [4.0, 4.0, 0.0, 1.0]])
>>> b_eq = np.array([60.0, 60.0])
>>> x0_bounds = (0, None)
>>> x1_bounds = (0, 5.0)
>>> x2_bounds = (-np.inf, 0.5)  # +/- np.inf can be used instead of None
>>> x3_bounds = (-3.0, None)
>>> bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
>>> result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
>>> print(result.message)
The problem is infeasible. (HiGHS Status 8: model_status is Infeasible; primal_status is None)

Результат утверждает, что наша задача несовместна, то есть не существует вектора решения, удовлетворяющего всем ограничениям. Это не обязательно означает, что мы сделали что-то не так; некоторые задачи действительно несовместны. Предположим, однако, что мы решим, что наше ограничение на границу \(x_1\) был слишком строгим и его можно ослабить до \(0 \leq x_1 \leq 6\). После корректировки нашего кода x1_bounds = (0, 6) чтобы отразить изменение и выполнить его снова:

>>> x1_bounds = (0, 6)
>>> bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
>>> result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
>>> print(result.message)
Optimization terminated successfully. (HiGHS Status 7: Optimal)

Результат показывает, что оптимизация прошла успешно. Мы можем проверить значение целевой функции (result.fun) такой же как \(c^Tx\):

>>> x = np.array(result.x)
>>> obj = result.fun
>>> print(c @ x)
-505.97435889013434  # may vary
>>> print(obj)
-505.97435889013434  # may vary

Мы также можем проверить, что все ограничения удовлетворяются в разумных пределах:

>>> print(b_ub - (A_ub @ x).flatten())  # this is equivalent to result.slack
[ 6.52747190e-10, -2.26730279e-09]  # may vary
>>> print(b_eq - (A_eq @ x).flatten())  # this is equivalent to result.con
[ 9.78840831e-09, 1.04662945e-08]]  # may vary
>>> print([0 <= result.x[0], 0 <= result.x[1] <= 6.0, result.x[2] <= 0.5, -3.0 <= result.x[3]])
[True, True, True, True]

Задачи назначения

Пример задачи линейного назначения

Рассмотрим задачу выбора студентов для команды плавания в комбинированной эстафете. У нас есть таблица, показывающая время для каждого стиля плавания пяти студентов:

Стьюдент	обратный гребок	брасс	butterfly	freestyle
A	43.5	47.1	48.4	38.2
B	45.5	42.1	49.6	36.8
C	43.4	39.1	42.1	43.2
D	46.5	44.1	44.5	41.2
E	46.3	47.8	50.4	37.2

Нам нужно выбрать студента для каждого из четырёх стилей плавания так, чтобы общее время эстафеты было минимальным. Это типичная задача линейного назначения. Мы можем использовать linear_sum_assignment чтобы решить её.

Задача о линейном назначении является одной из самых известных задач комбинаторной оптимизации. Дана "матрица затрат" \(C\), задача заключается в выборе

• ровно один элемент из каждой строки

• без выбора более одного элемента из любого столбца

• таким образом, чтобы сумма выбранных элементов была минимальна

Другими словами, нам нужно назначить каждую строку одному столбцу так, чтобы сумма соответствующих элементов была минимальной.

Формально, пусть \(X\) будет булевой матрицей, где \(X[i,j] = 1\) тогда и только тогда, когда строка \(i\) is assigned to column \(j\)Тогда оптимальное назначение имеет стоимость

\[\min \sum_i \sum_j C_{i,j} X_{i,j}\]

Первый шаг — определить матрицу затрат. В этом примере мы хотим назначить каждому стилю плавания студента. linear_sum_assignment способен назначить каждую строку матрицы затрат столбцу. Поэтому для формирования матрицы затрат таблицу выше нужно транспонировать так, чтобы строки соответствовали стилям плавания, а столбцы — студентам:

>>> import numpy as np
>>> cost = np.array([[43.5, 45.5, 43.4, 46.5, 46.3],
...                  [47.1, 42.1, 39.1, 44.1, 47.8],
...                  [48.4, 49.6, 42.1, 44.5, 50.4],
...                  [38.2, 36.8, 43.2, 41.2, 37.2]])

Мы можем решить задачу назначения с помощью linear_sum_assignment:

>>> from scipy.optimize import linear_sum_assignment
>>> row_ind, col_ind = linear_sum_assignment(cost)

The row_ind и col_ind являются оптимально назначенными индексами матрицы матрицы затрат:

>>> row_ind
array([0, 1, 2, 3])
>>> col_ind
array([0, 2, 3, 1])

Оптимальное назначение:

>>> styles = np.array(["backstroke", "breaststroke", "butterfly", "freestyle"])[row_ind]
>>> students = np.array(["A", "B", "C", "D", "E"])[col_ind]
>>> dict(zip(styles, students))
{'backstroke': 'A', 'breaststroke': 'C', 'butterfly': 'D', 'freestyle': 'B'}

Оптимальное общее время комбинированной эстафеты:

>>> cost[row_ind, col_ind].sum()
163.89999999999998

Обратите внимание, что этот результат не совпадает с суммой минимальных времен для каждого стиля плавания:

>>> np.min(cost, axis=1).sum()
161.39999999999998

потому что студент "C" - лучший пловец в обоих стилях "брасс" и "баттерфляй". Мы не можем назначить студента "C" на оба стиля, поэтому мы назначили студента C на стиль "брасс" и D на стиль "баттерфляй", чтобы минимизировать общее время.

Ссылки

Дополнительная литература и связанное программное обеспечение, такое как Newton-Krylov [KK], PETSc [PP], и PyAMG [AMG]:

[KK]

D.A. Knoll и D.E. Keyes, «Методы Ньютона-Крылова без якобиана», J. Comp. Phys. 193, 357 (2004). DOI:10.1016/j.jcp.2003.08.010

[PP]

PETSc https://www.mcs.anl.gov/petsc/ и его привязки Python https://bitbucket.org/petsc/petsc4py/

[AMG]

PyAMG (алгебраические многосеточные предобусловливатели/решатели) pyamg/pyamg#issues

Смешанное целочисленное линейное программирование

Пример задачи о рюкзаке

Задача о рюкзаке — хорошо известная комбинаторная оптимизационная задача. Дано множество предметов, каждый с размером и ценностью. Задача заключается в выборе предметов, максимизирующих общую ценность при условии, что общий размер не превышает определенный порог.

Формально, пусть

• \(x_i\) будет логической переменной, указывающей, затронут ли элемент \(i\) включен в рюкзак,

• \(n\) будет общим количеством элементов,

• \(v_i\) будет значением элемента \(i\),

• \(s_i\) будет размером элемента \(i\), и

• \(C\) будет вместимостью рюкзака.

Тогда задача заключается в следующем:

\[\max \sum_i^n v_{i} x_{i}\]

\[\text{subject to} \sum_i^n s_{i} x_{i} \leq C, x_{i} \in {0, 1}\]

Хотя целевая функция и ограничения неравенства линейны в переменные решения \(x_i\), это отличается от типичной задачи линейного программирования тем, что переменные решения могут принимать только целочисленные значения. В частности, наши переменные решения могут быть только \(0\) или \(1\), поэтому это известно как бинарная целочисленная линейная программа (BILP). Такая задача относится к более широкому классу смешанные целочисленные линейные программы (MILPs), которые мы можем решить с помощью milp.

В нашем примере есть 8 элементов для выбора, и размер и значение каждого указаны следующим образом.

>>> import numpy as np
>>> from scipy import optimize
>>> sizes = np.array([21, 11, 15, 9, 34, 25, 41, 52])
>>> values = np.array([22, 12, 16, 10, 35, 26, 42, 53])

Нам нужно ограничить наши восемь переменных решения двоичными значениями. Мы делаем это путем добавления Bounds: MAINT/ENH: stats.multivariate_normal.rvs: исправление формы и скорости… \(0\) и \(1\), и мы применяем ограничения «целочисленности», чтобы гарантировать, что они либо \(0\) или \(1\).

>>> bounds = optimize.Bounds(0, 1)  # 0 <= x_i <= 1
>>> integrality = np.full_like(values, True)  # x_i are integers

Ограничение вместимости рюкзака задаётся с использованием LinearConstraint.

>>> capacity = 100
>>> constraints = optimize.LinearConstraint(A=sizes, lb=0, ub=capacity)

Если мы следуем обычным правилам линейной алгебры, вход A должна быть двумерной матрицей, а нижняя и верхняя границы lb и ub должны быть одномерными векторами, но LinearConstraint снисходителен, пока входные данные могут быть транслированы к согласованным формам.

Используя определенные выше переменные, мы можем решить задачу о рюкзаке с помощью milp. Обратите внимание, что milp минимизирует целевую функцию, но мы хотим максимизировать общее значение, поэтому устанавливаем c должны быть отрицательными значениями.

>>> from scipy.optimize import milp
>>> res = milp(c=-values, constraints=constraints,
...            integrality=integrality, bounds=bounds)

Давайте проверим результат:

>>> res.success
True
>>> res.x
array([1., 1., 0., 1., 1., 1., 0., 0.])

Это означает, что мы должны выбрать элементы 1, 2, 4, 5, 6 для оптимизации общей стоимости при ограничении на размер. Обратите внимание, что это отличается от того, что мы получили бы, если бы решили релаксация линейного программирования (без ограничений целочисленности ) и попытался округлить переменные решения.

>>> from scipy.optimize import milp
>>> res = milp(c=-values, constraints=constraints,
...            integrality=False, bounds=bounds)
>>> res.x
array([1.        , 1.        , 1.        , 1.        ,
       0.55882353, 1.        , 0.        , 0.        ])

Если бы мы округлили это решение до array([1., 1., 1., 1., 1., 1., 0., 0.]), наш рюкзак превысил бы ограничение по вместимости, тогда как если бы мы округлили вниз до array([1., 1., 1., 1., 0., 1., 0., 0.]), мы бы получили субоптимальное решение.

Для дополнительных руководств по MILP см. Jupyter notebooks в SciPy Cookbooks:

• Программа сжатого зондирования l1

• Программа сжатого зондирования l0

Поддержка параллельного выполнения

Некоторые методы оптимизации SciPy, такие как differential_evolution, предлагают параллелизацию через использование workers ключевое слово.

Для differential_evolution в алгоритме есть два уровня циклов (итераций). Внешний цикл представляет последовательные поколения популяции. Этот цикл не может быть распараллелен. Для данного поколения генерируются кандидатные решения, которые должны сравниваться с существующими членами популяции. Пригодность кандидатного решения может быть вычислена в цикле, но также возможно распараллелить вычисление.

Параллелизация также возможна в других алгоритмах оптимизации. Например, в различных minimize методы численного дифференцирования используются для оценки производных. Для простого расчета градиента с использованием двухточечных прямых разностей всего N + 1 должны быть выполнены вычисления целевой функции, где N это количество параметров. Это просто небольшие возмущения вокруг заданного местоположения (the +1). Те N + 1 вычисления также распараллеливаемы. Вычисление численных производных используется алгоритмом минимизации для генерации новых шагов.

Каждый алгоритм оптимизации работает по-разному, но у них часто есть места, где требуются множественные вычисления целевой функции, прежде чем алгоритм переходит к следующему действию. Именно эти места можно распараллелить. Поэтому существуют общие характеристики в том, как workers используется. Эти общие черты описаны ниже.

Если указано целое число, то multiprocessing.Pool создаётся, с map метод, используемый для оценки решений параллельно. При таком подходе обязательно, чтобы целевая функция была pickleable. Лямбда-функции не соответствуют этому требованию.

>>> import numpy as np
>>> from scipy.optimize import rosen, differential_evolution, Bounds
>>> bnds = Bounds([0., 0., 0.], [10., 10., 10.])
>>> res = differential_evolution(rosen, bnds, workers=2, updating='deferred')

Также возможно использовать вызываемый объект, подобный map, в качестве рабочего. Здесь функция, подобная map, предоставляется серией векторов, которые предоставляет алгоритм оптимизации. Функция, подобная map, должна оценить каждый вектор по целевой функции. В следующем примере мы используем multiprocessing.Pool как map-подобный. Как и прежде, целевая функция все еще должна быть сериализуемой. Этот пример семантически идентичен предыдущему примеру.

>>> from multiprocessing import Pool
>>> with Pool(2) as pwl:
...     res = differential_evolution(rosen, bnds, workers=pwl.map, updating='deferred')

Использование этого шаблона может быть преимуществом, потому что Pool можно повторно использовать для дальнейших вычислений — создание этих объектов требует значительных накладных расходов. Альтернативы multiprocessing.Pool включать mpi4py пакет, который позволяет параллельную обработку на кластерах.

В Scipy 1.16.0 workers ключевое слово было введено для выбранных minimize методов. Здесь параллелизация обычно применяется во время численного дифференцирования. Можно использовать любой из двух подходов, описанных выше, хотя настоятельно рекомендуется предоставлять вызываемый объект, подобный map, из-за накладных расходов на создание новых процессов. Увеличение производительности будет достигнуто только если целевая функция дорога в вычислении. Давайте сравним, насколько параллелизация может помочь по сравнению с последовательной версией. Чтобы имитировать медленную функцию, мы используем time пакет.

>>> import time
>>> def slow_func(x):
...     time.sleep(0.0002)
...     return rosen(x)

Сначала рассмотрим последовательную минимизацию:

In [1]: rng = np.random.default_rng()

In [2]: x0 = rng.uniform(low=0.0, high=10.0, size=(20,))

In [3]: %timeit minimize(slow_func, x0, method='L-BFGS-B')  # serial approach
365 ms ± 6.17 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)  # may vary

Теперь параллельная версия:

In [4]: with Pool() as pwl:  # parallel approach
...         %timeit minimize(slow_func, x0, method='L-BFGS-B', options={'workers':pwl.map})
70.5 ms ± 146 μs per loop (mean ± std. dev. of 7 runs, 1 loop each)  # may vary

Если целевую функцию можно векторизовать, то можно использовать map-подобную функцию, чтобы воспользоваться преимуществами векторизации во время вычисления функции. Векторизация означает, что целевая функция может выполнить необходимые вычисления за один (а не несколько) вызов, что обычно очень эффективно:

In [5]: def vectorized_maplike(fun, iterable):
...         arr = np.array([i for i in iter(iterable)])   # arr.shape = (S, N)
...         arr_t = arr.T                                 # arr_t.shape = (N, S)
...         r = slow_func(arr_t)                          # calculation vectorized over S
...         return r

In [6]: %timeit minimize(slow_func, x0, method='L-BFGS-B', options={'workers':vectorized_maplike})
38.9 ms ± 734 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)  # may vary

Есть несколько важных моментов, которые следует отметить в этом примере:

• Итерируемый объект представляет серию векторов параметров, которые алгоритм желает оценить.

• Итерируемый объект сначала преобразуется в итератор, а затем в массив через списковое включение. Это позволяет итерируемому объекту быть генератором, списком, массивом и т.д.

• Внутри map-подобного вычисление выполняется с использованием slow_func вместо использования fun. Функция, подобная map, фактически снабжается обернутой версией целевой функции. Обертка используется для обнаружения различных типов распространенных ошибок пользователя, включая проверку, возвращает ли целевая функция скаляр. Если fun используется, тогда RuntimeError приведёт к тому, что fun(arr_t) будет одномерным массивом, а не скаляром. Поэтому мы используем slow_func напрямую.

• arr.T отправляется в целевую функцию. Это потому, что arr.shape == (S, N), где S это количество векторов параметров для оценки, а N это количество переменных. Для slow_func векторизация происходит на (N, S) массивы формы.

• Этот подход не требуется для differential_evolution поскольку этот минимизатор уже имеет ключевое слово для векторизации.