scipy.signal.ShortTimeFFT.

спектрограмма

ShortTimeFFT.спектрограмма(x, y=None, detr=None, *, p0=None, p1=None, k_offset=0, дополнение='zeros', ось=-1)

Вычислить спектрограмму или кросс-спектрограмму.

Спектрограмма — это абсолютный квадрат КПФ, т.е., она abs(S[q,p])**2 для заданных S[q,p] и, следовательно, всегда неотрицательна. Для двух STFT Sx[q,p], Sy[q,p], кросс-спектрограмма определяется как Sx[q,p] * np.conj(Sy[q,p]) и является комплекснозначной. Это удобная функция для вызова stft / stft_detrend, следовательно, все параметры обсуждаются там.

Параметры:

xnp.ndarray

Входной сигнал как массив с действительными или комплексными значениями. Для комплексных значений свойство fft_mode должно быть установлено в ‘twosided’ или ‘centered’.

ynp.ndarray

Второй входной сигнал той же формы, что и x. Если None, предполагается, что это x. Для комплексных значений свойство fft_mode должен быть установлен в ‘twosided’ или ‘centered’.

detr'linear' | 'constant' | Callable[[np.ndarray], np.ndarray] | None

Если 'constant', вычитается среднее значение; если установлено "linear", линейный тренд удаляется из каждого сегмента. Это достигается вызовом detrend. Если detr является функцией с одним параметром, detr применяется к каждому сегменту. Для None (по умолчанию), тренды не удаляются.

p0int | None

Первый элемент диапазона срезов для вычисления. Если None тогда оно устанавливается в p_min, который является наименьшим возможным срезом.

p1int | None

Конец массива. Если None затем p_max(n) используется.

k_offsetint

Индекс первого образца (t = 0) в x.

дополнение'zeros' | 'edge' | 'even' | 'odd'

Тип значений, которые добавляются, когда скользящее окно выходит за пределы нижнего или верхнего края входных данных x. Нули добавляются, если установлено значение по умолчанию 'zeros'. Для 'edge' либо первое, либо последнее значение из x используется. 'even' дополняет, отражая сигнал на первом или последнем отсчете, а 'odd' дополнительно умножает его на -1.

осьint

Ось x по которой вычисляется STFT. Если не указано, используется последняя ось.

Возвращает:

S_xynp.ndarray

Возвращается вещественный массив с неотрицательными значениями, если x is y или y является None. Размерность всегда на единицу больше, чем у x. Последняя ось всегда представляет временные срезы спектрограммы. ось определяет ось частоты (по умолчанию предпоследняя). Например, для одномерного x, возвращается комплексный 2D массив, где ось 0 представляет частоту, а ось 1 - временные срезы.

Смотрите также

stft

Выполнить кратковременное преобразование Фурье.

stft_detrend

STFT с трендом, вычтенным из каждого сегмента.

scipy.signal.ShortTimeFFT

Класс, к которому принадлежит этот метод.

Примечания

Кросс-спектрограмма может интерпретироваться как временно-частотный аналог кросс-спектральной плотности (см. csd). Абсолютный квадрат |Sxy|² кросс-спектрограммы Sxy деленные на спектрограммы Sxx и Syy может быть интерпретирован как когерентный спектрограмма Cxy := abs(Sxy)**2 / (Sxx*Syy), что является временно-частотным аналогом coherence.

Если STFT параметризован как унитарное преобразование, т.е., используя from_win_equals_dual, тогда значение скалярного произведения, а следовательно, и энергия, сохраняется.

Примеры

Попробуйте в вашем браузере!

Следующий пример показывает спектрограмму прямоугольного сигнала с изменяющейся частотой \(f_i(t)\) (отмечена зеленой пунктирной линией на графике) с частотой дискретизации 20 Гц. Используемое гауссово окно имеет длину 50 выборок или 2,5 с. Для ShortTimeFFT, параметр mfft=800 (коэффициент передискретизации 16) и hop интервал в 2 был выбран для получения достаточного количества точек.

Цветовая карта графика логарифмически масштабирована, так как спектральная плотность мощности измеряется в дБ. Временной интервал сигнала x обозначено вертикальными пунктирными линиями, а затененные области указывают на наличие граничных эффектов.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import square, ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T_x, N = 1 / 20, 1000  # 20 Hz sampling rate for 50 s signal
>>> t_x = np.arange(N) * T_x  # time indexes for signal
>>> f_i = 5e-3*(t_x - t_x[N // 3])**2 + 1  # varying frequency
>>> x = square(2*np.pi*np.cumsum(f_i)*T_x)  # the signal
...
>>> g_std = 12  # standard deviation for Gaussian window in samples
>>> win = gaussian(50, std=g_std, sym=True)  # symmetric Gaussian wind.
>>> SFT = ShortTimeFFT(win, hop=2, fs=1/T_x, mfft=800, scale_to='psd')
>>> Sx2 = SFT.spectrogram(x)  # calculate absolute square of STFT
...
>>> fig1, ax1 = plt.subplots(figsize=(6., 4.))  # enlarge plot a bit
>>> t_lo, t_hi = SFT.extent(N)[:2]  # time range of plot
>>> ax1.set_title(rf"Spectrogram ({SFT.m_num*SFT.T:g}$\,s$ Gaussian " +
...               rf"window, $\sigma_t={g_std*SFT.T:g}\,$s)")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({SFT.p_num(N)} slices, " +
...                rf"$\Delta t = {SFT.delta_t:g}\,$s)",
...         ylabel=f"Freq. $f$ in Hz ({SFT.f_pts} bins, " +
...                rf"$\Delta f = {SFT.delta_f:g}\,$Hz)",
...         xlim=(t_lo, t_hi))
>>> Sx_dB = 10 * np.log10(np.fmax(Sx2, 1e-4))  # limit range to -40 dB
>>> im1 = ax1.imshow(Sx_dB, origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='magma')
>>> ax1.plot(t_x, f_i, 'g--', alpha=.5, label='$f_i(t)$')
>>> fig1.colorbar(im1, label='Power Spectral Density ' +
...                          r"$20\,\log_{10}|S_x(t, f)|$ in dB")
...
>>> # Shade areas where window slices stick out to the side:
>>> for t0_, t1_ in [(t_lo, SFT.lower_border_end[0] * SFT.T),
...                  (SFT.upper_border_begin(N)[0] * SFT.T, t_hi)]:
...     ax1.axvspan(t0_, t1_, color='w', linewidth=0, alpha=.3)
>>> for t_ in [0, N * SFT.T]:  # mark signal borders with vertical line
...     ax1.axvline(t_, color='c', linestyle='--', alpha=0.5)
>>> ax1.legend()
>>> fig1.tight_layout()
>>> plt.show()

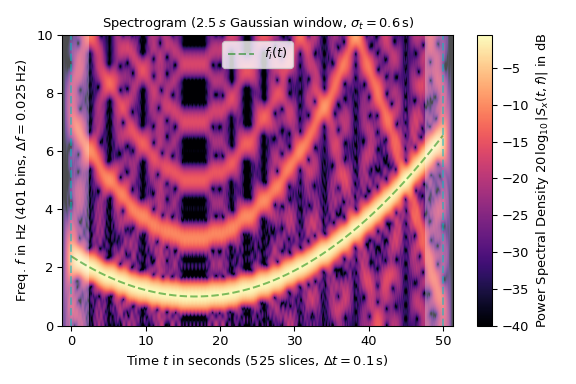
Логарифмическое масштабирование выявляет нечётные гармоники прямоугольной волны, которые отражаются на частоте Найквиста 10 Гц. Этот эффект наложения спектров также является основным источником шумовых артефактов на графике.

НазадОткрыть во вкладке