scipy.signal.

когерентность

scipy.signal.когерентность(x, y, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', ось=-1)

Оцените оценку квадрата величины когерентности, Cxy, дискретных сигналов X и Y с использованием метода Уэлча.

Cxy = abs(Pxy)**2/(Pxx*Pyy), где Pxx и Pyy являются оценками спектральной плотности мощности X и Y, и Pxy является оценкой взаимной спектральной плотности X и Y.

Параметры:

xarray_like

Временной ряд значений измерений

yarray_like

Временной ряд значений измерений

fsfloat, опционально

Частота дискретизации x и y временные ряды. По умолчанию равно 1.0.

windowstr или tuple или array_like, опционально

Желаемое окно для использования. Если window является строкой или кортежем, он передаётся в get_window для генерации значений окна, которые по умолчанию являются DFT-чётными. См. get_window для списка окон и требуемых параметров. Если window если это array_like, он будет использоваться напрямую как окно, и его длина должна быть nperseg. По умолчанию используется окно Ханна.

npersegint, необязательный

Длина каждого сегмента. По умолчанию None, но если window является строкой или кортежем, устанавливается в 256, а если window является array_like, устанавливается в длину окна.

noverlap: int, optional

Количество точек перекрытия между сегментами. Если None, noverlap = nperseg // 2. По умолчанию None.

nfftint, необязательный

Длина БПФ, используемая, если требуется дополненное нулями БПФ. Если None, длина БПФ равна nperseg. По умолчанию None.

detrendstr или функция или False, опционально

Определяет, как удалять тренд в каждом сегменте. Если detrend является строкой, она передается как тип аргумент для detrend функция. Если это функция, она принимает сегмент и возвращает сегмент с удалённым трендом. Если detrend является False, детрендинг не выполняется. По умолчанию 'constant'.

осьint, необязательный

Ось, по которой вычисляется когерентность для обоих входов; по умолчанию используется последняя ось (т.е. axis=-1).

Возвращает:

fndarray

Массив частот выборки.

Cxyndarray

Квадрат модуля когерентности x и y.

Смотрите также

periodogram

Простой, опционально модифицированный периодограмм

lombscargle

Периодограмма Ломба-Скаргла для неравномерно дискретизированных данных

welch

Спектральная плотность мощности методом Уэлча.

csd

Спектральная плотность мощности методом Уэлча.

Примечания

Подходящее количество перекрытия будет зависеть от выбора окна и ваших требований. Для окна Ханна по умолчанию перекрытие в 50% является разумным компромиссом между точной оценкой мощности сигнала и избеганием повторного учета данных. Более узкие окна могут требовать большего перекрытия.

Добавлено в версии 0.16.0.

Ссылки

[1]

P. Welch, "Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени коротких модифицированных периодограмм", IEEE Trans. Audio Electroacoust. том 15, стр. 70-73, 1967.

[2]

Стойка, Петре, и Рэндольф Мозес, «Спектральный анализ сигналов», Prentice Hall, 2005

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Сгенерируйте два тестовых сигнала с некоторыми общими характеристиками.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 20
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> b, a = signal.butter(2, 0.25, 'low')
>>> x = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> y = signal.lfilter(b, a, x)
>>> x += amp*np.sin(2*np.pi*freq*time)
>>> y += rng.normal(scale=0.1*np.sqrt(noise_power), size=time.shape)

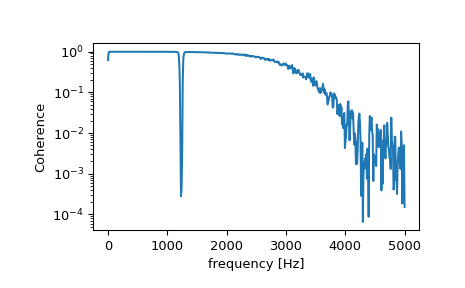
Вычисление и построение когерентности.

>>> f, Cxy = signal.coherence(x, y, fs, nperseg=1024)
>>> plt.semilogy(f, Cxy)
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Coherence')
>>> plt.show()

НазадОткрыть во вкладке