scipy.signal.

closest_STFT_dual_window#

scipy.signal.closest_STFT_dual_window(win, hop, desired_dual=None, *, масштабированный=True)[источник]#

Вычисление двойственного окна STFT для заданного окна, наиболее близкого к желаемому двойственному окну.

Для заданного окна короткого преобразования Фурье win увеличивается на hop образцов, вычисляется двойное окно, которое минимизирует abs(dual_win - desired_dual)**2 когда масштабированный является False. Для масштабированный установлено в True, abs(alpha*dual_win - desired_dual)**2 минимизируется с помощью alpha являясь оптимальным коэффициентом масштабирования. A ValueError возникает, если не удается определить допустимое двойное окно.

Параметры:

winnp.ndarray: Окно должно быть вещественным или комплексным одномерным массивом.
hopint: Приращение в выборках, на которое окно сдвигается на каждом шаге.
desired_dual: np.ndarray | None: Желаемое двойное окно должно быть одномерным массивом той же длины, что и win. Если установлено в None (по умолчанию), затем desired_dual предполагается прямоугольным окном, т.е., np.ones_like(win).
масштабированныйbool: Если установлено (по умолчанию), вычисляется ближайшая масштабированная версия вместо ближайшего двойственного окна.

Возвращает:

dual_winnp.ndarray: Двойное окно alpha*win (с интервалом хопа hop), который ближе всего к desired_dual. Обратите внимание, что двойное окно win является dual_win/alpha и что двойное окно dual_win является alpha*win. dual_win имеет ту же форму, что и win и desired_win.
alphafloat | complex: Масштабный коэффициент для win. Он всегда равен единице, если масштабированный установлено в False.

Смотрите также

ShortTimeFFT: Кратковременное преобразование Фурье, способное использовать двойное окно для вычисления обратного преобразования.
ShortTimeFFT.from_win_equals_dual: Создать экземпляр, где окно и его двойник равны.

Примечания

Для заданного окна и hop интервал, все возможные двойные окна выражаются через hop линейные условия уравнения (24) в Кратковременное преобразование Фурье раздел Руководство пользователя SciPy. Следовательно, уменьшение hop, увеличивает количество степеней свободы множества всех возможных двойных окон, улучшая способность лучше аппроксимировать desired_dual.

Эта функция также может использоваться для определения окон, которые удовлетворяют так называемому условию "Constant OverLap Add" (COLA) [1]. Утверждается, что суммирование всех значений касающихся окон в любой заданной позиции выборки даёт ту же константу \(\alpha\). Ур. (24) показывает, что это эквивалентно наличию прямоугольного двойного окна, т.е. двойственное окно является alpha*np.ones(m).

Некоторые примеры окон, удовлетворяющих COLA (взяты из [2]):

Прямоугольное окно при перекрытии 0, 1/2, 2/3, 3/4, …
Окно Бартлетта при перекрытии 1/2, 3/4, 5/6, …
Окно Ханна на 1/2, 2/3, 3/4, …
Любое окно семейства Блэкмана с перекрытием 2/3
Любое окно с hop=1

Ссылки

[1]

Джулиус О. Смит III, "Спектральная обработка аудиосигналов", онлайн-книга, 2011, https://www.dsprelated.com/freebooks/sasp/

[2]

G. Heinzel, A. Ruediger и R. Schilling, “Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new at-top windows”, 2002, http://hdl.handle.net/11858/00-001M-0000-0013-557A-5

Примеры

Покажем, что окно Бартлетта с 75% перекрытием удовлетворяет условию COLA:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import closest_STFT_dual_window, windows
...
>>> m = 24
>>> win, w_rect = windows.bartlett(m, sym=False), np.ones(m)
>>> d_win, alpha = closest_STFT_dual_window(win, m//4, w_rect, scaled=True)
>>> print(f"COLA: {np.allclose(d_win, w_rect*alpha)}, {alpha = :g}")
COLA: True, alpha = 0.5

Мы также можем определить, для каких интервалов скачка выполняется условие COLA:

>>> hops, deviations, alphas = np.arange(1, 16, dtype=int), [], []
>>> for h_ in hops:
...     w_cola, alpha = closest_STFT_dual_window(w_rect, h_, win, scaled=True)
...     deviations.append(np.linalg.norm(w_cola - win*alpha))
...     alphas.append(alpha)
...
>>> fg0, (ax0, ax1) = plt.subplots(2, 1, sharex='all', tight_layout=True)
>>> ax0.set_title(f"COLA Window closest to a {m}-Sample Bartlett Window")
>>> ax0.set(ylabel=r"$||w_\text{cola}-\alpha w||$", xlim=(0, hops[-1]-.5))
>>> ax1.set(xlabel="Hop Interval", ylabel=r"Scaling factor $\alpha$",
...         ylim=(0, 1.25))
>>> ax0.plot(hops, deviations, 'C0.-')
>>> ax1.plot(hops, alphas, 'C1.-')
>>> for ax_ in (ax0, ax1):
...     ax_.grid()
>>> plt.show()

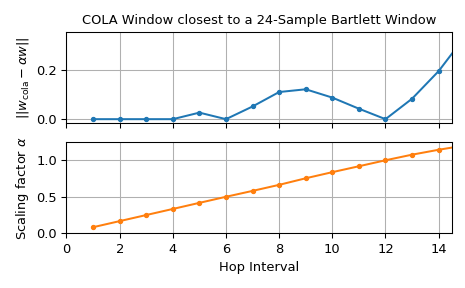
../../_images/scipy-signal-closest_STFT_dual_window-1_00_00.png

Нижний график показывает вычисленный масштабный коэффициент \(\alpha\) для разных hops тогда как верхний отображает \(L^2\)-норма разницы между масштабированным окном Бартлетта и вычисленным окном. Поскольку для hops от 1 до 4, а также для 6 и 12 \(L^2\)-норма разности практически равна нулю, условие COLA выполняется для них.