scipy.signal.

stft#

scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, границе='zeros', дополненный=True, ось=-1, масштабирование='spectrum')[источник]#

Вычислите кратковременное преобразование Фурье (устаревшая функция).

STFT можно использовать как способ количественной оценки изменения частотного и фазового содержания нестационарного сигнала во времени.

Наследие

Эта функция считается устаревшей и больше не будет получать обновления. Хотя в настоящее время у нас нет планов по ее удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. ShortTimeFFT является более новой реализацией STFT / ISTFT с большим количеством функций. A сравнение между реализациями можно найти в Кратковременное преобразование Фурье раздел Руководство пользователя SciPy.

Параметры:

xarray_like: Временной ряд значений измерений
fsfloat, опционально: Частота дискретизации x временной ряд. По умолчанию 1.0.
windowstr или tuple или array_like, опционально: Желаемое окно для использования. Если window является строкой или кортежем, он передаётся в get_window для генерации значений окна, которые по умолчанию являются DFT-чётными. См. get_window для списка окон и требуемых параметров. Если window если это array_like, он будет использоваться напрямую как окно, и его длина должна быть nperseg. По умолчанию используется окно Ханна.
npersegint, необязательный: Длина каждого сегмента. По умолчанию 256.
noverlapint, необязательный: Количество точек перекрытия между сегментами. Если None, noverlap = nperseg // 2. По умолчанию None. При указании ограничение COLA должно выполняться (см. примечания ниже).
nfftint, необязательный: Длина БПФ, используемая, если требуется дополненное нулями БПФ. Если None, длина БПФ равна nperseg. По умолчанию None.
detrendstr или функция или False, опционально: Определяет, как удалять тренд в каждом сегменте. Если detrend является строкой, она передается как тип аргумент для detrend функция. Если это функция, она принимает сегмент и возвращает сегмент с удалённым трендом. Если detrend является False, детрендинг не выполняется. По умолчанию False.
return_onesidedbool, необязательно: Если True, возвращает односторонний спектр для реальных данных. Если False возвращает двусторонний спектр. По умолчанию True, но для комплексных данных всегда возвращается двусторонний спектр.
границеstr или None, опционально: Определяет, расширяется ли входной сигнал на обоих концах, и как генерируются новые значения, чтобы центрировать первый сегмент с окном на первой входной точке. Это позволяет восстановить первую входную точку, когда используемая оконная функция начинается с нуля. Допустимые варианты: ['even', 'odd', 'constant', 'zeros', None]. По умолчанию 'zeros', для расширения нулевым заполнением. Т.е. [1, 2, 3, 4] расширяется до [0, 1, 2, 3, 4, 0] для nperseg=3.
дополненныйbool, необязательно: Определяет, дополняется ли входной сигнал нулями в конце, чтобы сигнал точно вписывался в целое число сегментов окна, чтобы весь сигнал был включен в выходные данные. По умолчанию True. Дополнение происходит после расширения границ, если границе не является None, и дополненный является True, как это установлено по умолчанию.
осьint, необязательный: Ось, вдоль которой вычисляется STFT; по умолчанию — по последней оси (т.е. axis=-1).
scaling: {‘spectrum’, ‘psd’}: Масштабирование по умолчанию 'spectrum' позволяет каждой частотной линии Zxx интерпретироваться как спектр амплитуд. Опция 'psd' масштабирует каждую линию до спектральной плотности мощности - это позволяет вычислить энергию сигнала путём численного интегрирования по abs(Zxx)**2.

Добавлено в версии 1.9.0.

Возвращает:

fndarray: Массив частот выборки.
tndarray: Массив времен сегментов.
Zxxndarray: STFT от x. По умолчанию последняя ось Zxx соответствует временам сегментов.

Смотрите также

istft: Обратное коротковременное преобразование Фурье
ShortTimeFFT: Новая реализация STFT/ISTFT с большим количеством функций.
check_COLA: Проверить, выполняется ли ограничение Constant OverLap Add (COLA)
check_NOLA: Проверить, выполняется ли ограничение Nonzero Overlap Add (NOLA)
welch: Спектральная плотность мощности методом Уэлча.
spectrogram: Спектрограмма методом Уэлча.
csd: Спектральная плотность мощности методом Уэлча.
lombscargle: Периодограмма Ломба-Скаргла для неравномерно дискретизированных данных

Примечания

Чтобы включить инверсию STFT через обратное STFT в istft, оконное преобразование сигнала должно удовлетворять условию "Ненулевого Перекрытия с Суммированием" (NOLA), и входной сигнал должен иметь полное покрытие оконным преобразованием (т.е. (x.shape[axis] - nperseg) % (nperseg-noverlap) == 0). дополненный аргумент может быть использован для достижения этого.

Для сигнала во временной области \(x[n]\), окно \(w[n]\), и размер шага \(H\) = nperseg - noverlap, оконный кадр во временном индексе \(t\) задается формулой

\[x_{t}[n]=x[n]w[n-tH]\]

Уравнение реконструкции с наложением-сложением (OLA) задаётся как

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

Ограничение NOLA гарантирует, что каждый нормировочный член, появляющийся в знаменателе уравнения реконструкции OLA, ненулевой. Независимо от выбора window, nperseg, и noverlap удовлетворяющие этому ограничению могут быть проверены с помощью check_NOLA.

Добавлено в версии 0.19.0.

Ссылки

[1]

Оппенгейм, Алан В., Рональд В. Шафер, Джон Р. Бак "Обработка дискретных сигналов", Prentice Hall, 1999.

[2]

Дэниел В. Гриффин, Джей С. Лим «Оценка сигнала по модифицированному кратковременному преобразованию Фурье», IEEE 1984, 10.1109/TASSP.1984.1164317

Примеры

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Сгенерировать тестовый сигнал, синусоиду 2 В среднеквадратичных, частота которой медленно модулируется около 3 кГц, искаженную белым шумом экспоненциально убывающей амплитуды, дискретизированный на частоте 10 кГц.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.01 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> mod = 500*np.cos(2*np.pi*0.25*time)
>>> carrier = amp * np.sin(2*np.pi*3e3*time + mod)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> noise *= np.exp(-time/5)
>>> x = carrier + noise

Вычислить и построить амплитуду STFT.

>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000)
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

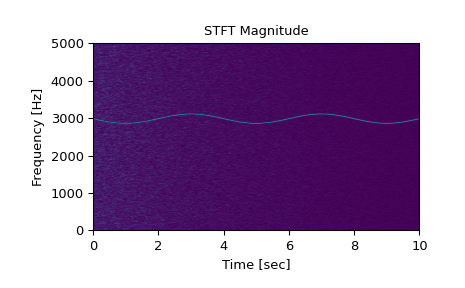
../../_images/scipy-signal-stft-1_00_00.png

Сравните энергию сигнала x с энергией его STFT:

>>> E_x = sum(x**2) / fs  # Energy of x
>>> # Calculate a two-sided STFT with PSD scaling:
>>> f, t, Zxx = signal.stft(x, fs, nperseg=1000, return_onesided=False,
...                         scaling='psd')
>>> # Integrate numerically over abs(Zxx)**2:
>>> df, dt = f[1] - f[0], t[1] - t[0]
>>> E_Zxx = sum(np.sum(Zxx.real**2 + Zxx.imag**2, axis=0) * df) * dt
>>> # The energy is the same, but the numerical errors are quite large:
>>> np.isclose(E_x, E_Zxx, rtol=1e-2)
True