scipy.signal.

freqs_zpk#

scipy.signal.freqs_zpk(z, p, k, worN=200)[источник]#

Вычислить частотную характеристику аналогового фильтра.

Учитывая нули z, полюсы p, и усиление k фильтра, вычислить его частотную характеристику:

           (jw-z[0]) * (jw-z[1]) * ... * (jw-z[-1])
H(w) = k * ----------------------------------------
           (jw-p[0]) * (jw-p[1]) * ... * (jw-p[-1])

Параметры:

zarray_like: Нули линейного фильтра
parray_like: Полюса линейного фильтра
kскаляр: Коэффициент усиления линейного фильтра
worN{None, int, array_like}, optional: Если None, то вычисляется на 200 частотах вокруг интересных частей кривой отклика (определяемых расположением полюсов и нулей). Если задано одно целое число, то вычисляется на таком количестве частот. В противном случае вычисляется отклик на заданных угловых частотах (например, рад/с) в worN.

Возвращает:

wndarray: Угловые частоты, на которых h было вычислено.
hndarray: Частотная характеристика.

Смотрите также

freqs: Вычислить частотную характеристику аналогового фильтра в TF-форме
freqz: Вычислить частотную характеристику цифрового фильтра в TF форме
freqz_zpk: Вычислить частотную характеристику цифрового фильтра в форме ZPK

Примечания

Добавлено в версии 0.19.0.

Примеры

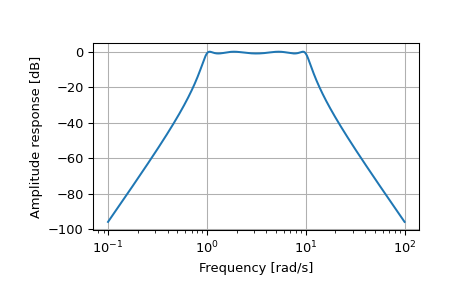
>>> import numpy as np
>>> from scipy.signal import freqs_zpk, iirfilter

>>> z, p, k = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1',
...                     output='zpk')

>>> w, h = freqs_zpk(z, p, k, worN=np.logspace(-1, 2, 1000))

>>> import matplotlib.pyplot as plt
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude response [dB]')
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-freqs_zpk-1.png