scipy.signal.

istft

scipy.signal.istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, input_onesided=True, границе=True, time_axis=-1, freq_axis=-2, масштабирование='spectrum')

Выполнить обратное кратковременное преобразование Фурье (устаревшая функция).

Наследие

Эта функция считается устаревшей и больше не будет получать обновления. Хотя в настоящее время у нас нет планов по ее удалению, мы рекомендуем, чтобы новый код использовал более современные альтернативы. ShortTimeFFT является более новой реализацией STFT / ISTFT с большим количеством функций. A сравнение между реализациями можно найти в Кратковременное преобразование Фурье раздел Руководство пользователя SciPy.

Параметры:

Zxxarray_like

STFT сигнала для восстановления. Если передан чисто вещественный массив, он будет приведен к комплексному типу данных.

fsfloat, опционально

Частота дискретизации временного ряда. По умолчанию 1.0.

windowstr или tuple или array_like, опционально

Желаемое окно для использования. Если window является строкой или кортежем, он передаётся в get_window для генерации значений окна, которые по умолчанию являются DFT-чётными. См. get_window для списка окон и требуемых параметров. Если window если это array_like, он будет использоваться непосредственно как окно, и его длина должна быть nperseg. По умолчанию используется окно Ханна. Должно соответствовать окну, использованному для генерации STFT для точной инверсии.

npersegint, необязательный

Количество точек данных, соответствующих каждому сегменту STFT. Этот параметр должен быть указан, если количество точек данных на сегмент нечётное, или если STFT был дополнен через nfft > nperseg. Если None, значение зависит от формы Zxx и input_onesided. Если input_onesided является True, nperseg=2*(Zxx.shape[freq_axis] - 1). В противном случае, nperseg=Zxx.shape[freq_axis]. По умолчанию None.

noverlapint, необязательный

Количество точек перекрытия между сегментами. Если None, половина длины сегмента. По умолчанию None. При указании ограничение COLA должно выполняться (см. примечания ниже) и должно соответствовать параметру, использованному для генерации STFT. По умолчанию None.

nfftint, необязательный

Количество точек БПФ, соответствующих каждому сегменту STFT. Этот параметр должен быть указан, если STFT был дополнен через nfft > nperseg. Если None, значения по умолчанию такие же, как для nperseg, подробно описанный выше, с одним исключением: если input_onesided равно True и nperseg==2*Zxx.shape[freq_axis] - 1, nfft также принимает это значение. Этот случай позволяет правильно инвертировать STFT нечетной длины без заполнения с помощью nfft=None. По умолчанию None.

input_onesidedbool, необязательно

Если True, интерпретировать входной массив как односторонние FFT, как возвращается stft с return_onesided=True и numpy.fft.rfft. Если False, интерпретировать входные данные как двустороннее БПФ. По умолчанию: True.

границеbool, необязательно

Определяет, был ли входной сигнал расширен на своих границах путем предоставления не-None boundary аргумент для stft. По умолчанию True.

time_axisint, необязательный

Где расположены временные сегменты STFT; по умолчанию последняя ось (т.е. axis=-1).

freq_axisint, необязательный

Где находится частотная ось STFT; по умолчанию это предпоследняя ось (т.е. axis=-2).

scaling: {‘spectrum’, ‘psd’}

Масштабирование по умолчанию 'spectrum' позволяет каждой частотной линии Zxx интерпретироваться как спектр амплитуд. Опция 'psd' масштабирует каждую линию до спектральной плотности мощности - это позволяет вычислить энергию сигнала путём численного интегрирования по abs(Zxx)**2.

Возвращает:

tndarray

Массив выходных времен данных.

xndarray

iSTFT от Zxx.

Смотрите также

stft

Кратковременное преобразование Фурье

ShortTimeFFT

Новая реализация STFT/ISTFT с большим количеством функций.

check_COLA

Проверить, выполняется ли ограничение Constant OverLap Add (COLA)

check_NOLA

Проверить, выполняется ли ограничение Nonzero Overlap Add (NOLA)

Примечания

Для того чтобы включить инверсию STFT через обратный STFT с istft, оконная обработка сигнала должна удовлетворять условию «ненулевого перекрытия с суммированием» (NOLA):

\[\sum_{t}w^{2}[n-tH] \ne 0\]

Это гарантирует, что нормировочные коэффициенты, появляющиеся в знаменателе уравнения реконструкции с перекрытием и сложением

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

не равны нулю. Ограничение NOLA можно проверить с помощью check_NOLA функция.

STFT, который был изменен (через маскирование или иначе), не гарантирует соответствие точно реализуемому сигналу. Эта функция реализует iSTFT через алгоритм оценки методом наименьших квадратов, подробно описанный в [2], который производит сигнал, минимизирующий среднеквадратичную ошибку между STFT возвращаемого сигнала и модифицированным STFT.

Добавлено в версии 0.19.0.

Ссылки

[1]

Оппенгейм, Алан В., Рональд В. Шафер, Джон Р. Бак "Обработка дискретных сигналов", Prentice Hall, 1999.

[2]

Дэниел В. Гриффин, Джей С. Лим «Оценка сигнала по модифицированному кратковременному преобразованию Фурье», IEEE 1984, 10.1109/TASSP.1984.1164317

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Сгенерировать тестовый сигнал, синусоидальную волну 2 Vrms на 50 Гц, искаженную белым шумом 0.001 V**2/Гц, дискретизированную на 1024 Гц.

>>> fs = 1024
>>> N = 10*fs
>>> nperseg = 512
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> carrier = amp * np.sin(2*np.pi*50*time)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> x = carrier + noise

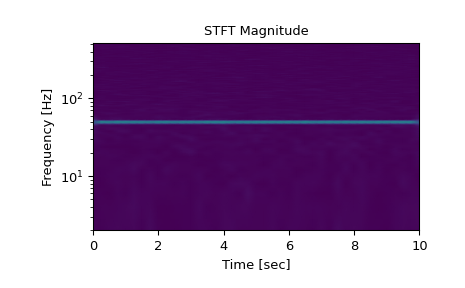
Вычислить STFT и построить график его амплитуды

>>> f, t, Zxx = signal.stft(x, fs=fs, nperseg=nperseg)
>>> plt.figure()
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.ylim([f[1], f[-1]])
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.yscale('log')
>>> plt.show()

Обнулить компоненты, которые составляют 10% или меньше от величины несущей, затем преобразовать обратно во временной ряд через обратное STFT

>>> Zxx = np.where(np.abs(Zxx) >= amp/10, Zxx, 0)
>>> _, xrec = signal.istft(Zxx, fs)

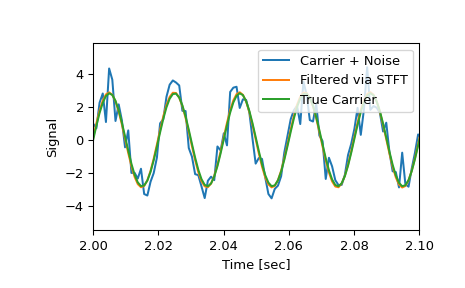
Сравните очищенный сигнал с исходным и истинным несущим сигналами.

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([2, 2.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()

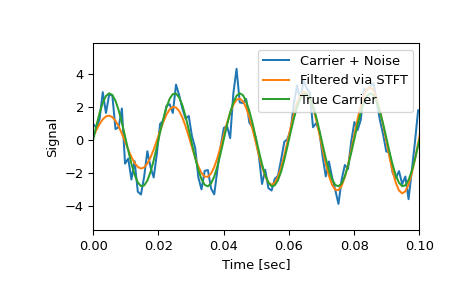
Обратите внимание, что очищенный сигнал начинается не так резко, как исходный, поскольку некоторые коэффициенты переходного процесса также были удалены:

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([0, 0.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()

НазадОткрыть во вкладке