scipy.special.

jvp#

scipy.special.jvp(v, z, n=1)[источник]#

Вычисляет производные функций Бесселя первого рода.

Вычислить n-ю производную функции Бесселя Jv относительно z.

Параметры:

varray_like или float: Порядок функции Бесселя
zкомплексный: Аргумент, в котором вычисляется производная; может быть вещественным или комплексным.
nint, по умолчанию 1: Порядок производной. Для 0 возвращает функцию Бесселя jv самого себя.

Возвращает:

скаляр или ndarray: Значения производной функции Бесселя.

Примечания

Производная вычисляется с использованием соотношения DLFM 10.6.7 [2].

Ссылки

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

[2]

Цифровая библиотека математических функций NIST. https://dlmf.nist.gov/10.6.E7

Примеры

Вычислить функцию Бесселя первого рода порядка 0 и её первые две производные в 1.

>>> from scipy.special import jvp
>>> jvp(0, 1, 0), jvp(0, 1, 1), jvp(0, 1, 2)
(0.7651976865579666, -0.44005058574493355, -0.3251471008130331)

Вычислить первую производную функции Бесселя первого рода для нескольких порядков в точке 1, предоставив массив для v.

>>> jvp([0, 1, 2], 1, 1)
array([-0.44005059,  0.3251471 ,  0.21024362])

Вычислить первую производную функции Бесселя первого рода порядка 0 в нескольких точках, предоставив массив для z.

>>> import numpy as np
>>> points = np.array([0., 1.5, 3.])
>>> jvp(0, points, 1)
array([-0.        , -0.55793651, -0.33905896])

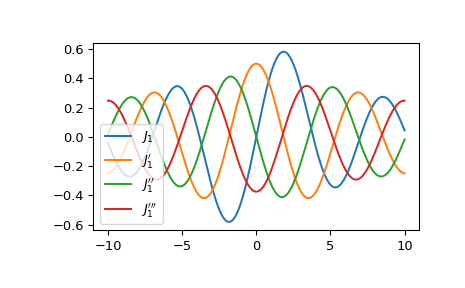
Построить функцию Бесселя первого рода порядка 1 и её первые три производные.

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-10, 10, 1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, jvp(1, x, 0), label=r"$J_1$")
>>> ax.plot(x, jvp(1, x, 1), label=r"$J_1'$")
>>> ax.plot(x, jvp(1, x, 2), label=r"$J_1''$")
>>> ax.plot(x, jvp(1, x, 3), label=r"$J_1'''$")
>>> plt.legend()
>>> plt.show()